一、组合数

1.递推式

$\displaystyle\binom{n}{m} = \displaystyle\binom{n - 1}{m - 1} + \displaystyle\binom{n - 1}{m}$

证：左边相当于从$n$个数中选$m$个数，右边枚举第$n$个数选不选。如果选，就从剩下$n - 1$个数中选$m - 1$个；如果不选，就从剩下$n - 1$个数中选$m$个。

2.对称性

$\displaystyle\binom{n}{m} = \displaystyle\binom{n}{n - m}$

证：左边相当于从$n$个数中选$m$个数留下，右边相当于从$n$个数中选$n - m$个数丢弃。

3.吸收/相伴等式

$\displaystyle\frac{\displaystyle\binom{n}{m}}{\displaystyle\binom{n - 1}{m - 1}} = \displaystyle\frac{n}{m}$

证：原式 $= \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!m!}}{\displaystyle\frac{(n - 1)!}{(n - 1 - m + 1)!(m - 1)!}}=\displaystyle\frac{\displaystyle\frac{n!}{m!}}{\displaystyle\frac{(n - 1)!}{(m - 1)!}} = \displaystyle\frac{n}{m}$

$\displaystyle\frac{\displaystyle\binom{n}{m}}{\displaystyle\binom{n - 1}{m}} = \displaystyle\frac{n}{n - m}$

证：原式 $= \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!m!}}{\displaystyle\frac{(n - 1)!}{(n - 1 - m)!m!}} = \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!}}{\displaystyle\frac{(n - 1)!}{(n - m - 1)!}} = \displaystyle\frac{n}{n - m}$

$\displaystyle\frac{\displaystyle\binom{n}{m}}{\displaystyle\binom{n}{m - 1}} = \displaystyle\frac{n - m + 1}{m}$

证：原式 $= \displaystyle\frac{\displaystyle\frac{n!}{(n - m)!m!}}{\displaystyle\frac{n!}{(n - m + 1)!(m - 1)!}} = \displaystyle\frac{(n - m + 1)!(m - 1)!}{(n - m)!m!} = \displaystyle\frac{n - m + 1}{m}$

4.上指标反转

$\displaystyle\binom{n}{m} = (-1)^m\displaystyle\binom{m - n - 1}{m}$

证：原式 $= \displaystyle\frac{n^{\displaystyle\underline{\displaystyle{m}}}}{m!} = (-1)^{m\displaystyle\frac{(-n)}{\displaystyle\overline{\displaystyle{m}}}}{m!} = (-1)^m\displaystyle\frac{(m - n - 1)^{\displaystyle\underline{\displaystyle{m}}}}{m!} = (-1)^m\displaystyle\binom{m - n - 1}{m}$

5.三项式系数恒等式

$\displaystyle\binom{n}{m}\displaystyle\binom{m}{k} = \displaystyle\binom{n}{k}\displaystyle\binom{n - k}{m - k}$

证：左边相当于从$n$个数中选$m$个数，再从这$m$个数中选$k$个数，右边相当于从$n$个数中选$k$个数，这些数一定包含在要选的$m$个数中，因此就只用在剩下$n - k$个数中选$m - k$个数。

6.上指标求和

$\displaystyle\sum_{i=0}^{n}\displaystyle\binom{i}{m} = \displaystyle\binom{n + 1}{m + 1}$

证：①原式 $= \displaystyle\sum_{i=m}^{{n}\displaystyle\frac{i}{\displaystyle\underline{\displaystyle{m}}}}{m!}$ (当$i \displaystyle\leq m$时，无法从$i$个数中选出$m$个数，因此省去) $= \displaystyle\frac{1}{m!}\displaystyle\sum_{i=m}^{n}i{\displaystyle\underline{\displaystyle{m}}}$ ($\displaystyle\frac{1}{m!}$与$i$无关，可以提出) = $\displaystyle\frac{1}{m!}[\displaystyle\frac{(n + 1)^{\displaystyle\underline{\displaystyle{m + 1}}}}{m + 1} - \displaystyle\frac{m^{\displaystyle\underline{\displaystyle{m + 1}}}}{m + 1}]$ (离散微积分，具体证明可见《离散微积分学习笔记》) $= \displaystyle\frac{(n + 1)^{\displaystyle\underline{\displaystyle{m + 1}}}}{(m + 1)!} = \displaystyle\binom{n + 1}{m + 1}$

②右边相当于从$n + 1$个数中选出$m + 1$个数，左边相当于确定了第$m + 1$个数的位置$i + 1$，要从前$i$个数中再选$m$个。

练习一

化简：$\displaystyle\sum_{i=0}^{m}\displaystyle\binom{n + i}{i}$

解：原式 $= \displaystyle\sum_{i=0}^m\binom{n + i}{n} $(对称性)$= \displaystyle\binom{n + m + 1}{n + 1}$(上指标求和)

7.下指标求和

$\displaystyle\sum_{i=0}^{n}\displaystyle\binom{n}{i} = 2^n$

证：①左边相当于从$n$个数中选任意个数，每个数都有选或不选两种方案，因此有$2^n$种方案。

②当二项式定理中$x$和$y$都为$1$，就可以得出此等式

例题一

一句话题意：给$q$组询问，每次给出$n, m$，求$\displaystyle\sum_{i=0}^{m}\displaystyle\binom{n}{i}$

$q, n, m \leq 10^5$，对$109 + 7$取模

解：把$n, m$看成区间，使用莫队算法(我不会qwq)：

$n \rightarrow n + 1$：$\displaystyle\sum_{i=0}^m\displaystyle\binom{n + 1}{i} = \displaystyle\sum_{i=0}^m\displaystyle\binom{n}{i} + \displaystyle\sum_{i=0}^m\displaystyle\binom{n - 1}{i} = 2\displaystyle\sum_{i=0}^m\displaystyle\binom{n}{i} - \displaystyle\binom{n}{m}$(两排错位相加，减掉最后一位)

$m \rightarrow m + 1$：$\displaystyle\sum_{i=0}^{m + 1}\displaystyle\binom{n}{i} = \displaystyle\sum_{i=0}^m\displaystyle\binom{n}{i} + \displaystyle\binom{n}{m + 1}$

8.下指标卷积 | 范德蒙德卷积

$\displaystyle\sum_{i=0}^{k}\displaystyle\binom{n}{i}\displaystyle\binom{m}{k - i} = \displaystyle\binom{n + m}{k}$

证：左边相当于从$n$个数中选$i$个数，再从$m$个数中选$k - i$个数，右边相当于从$n + m$个数中选$k$个数，两者意义相同

练习二|下指标点积

化简$\displaystyle\sum_{i=0}^{m}\displaystyle\binom{n}{i}\displaystyle\binom{m}{i}$

解：原式 $=\displaystyle\sum_{i=0}^{m}\displaystyle\binom{n}{i}\displaystyle\binom{m}{m - i}$(对称性) = $\displaystyle\binom{n + m}{m}$(下指标卷积)

9.上指标卷积

$\displaystyle\sum_{i=0}^{n}\displaystyle\binom{i}{a}\displaystyle\binom{n - i}{b} = \displaystyle\binom{n + 1}{a + b + 1}$

证：左边相当于在$n$个数中插入一个挡板，在挡板左边的数中选$a$个，在挡板右边的数中选$b$个，如果将挡板也看作一个数，那么就等于从$n + 1$个数中选$a + b + 1$个数，即右边的表达式

练习三

化简：$\displaystyle\sum_{i=m}^{n}(-1)i\displaystyle\binom{n}{i}\displaystyle\binom{i}{m}$

解：原式 $= \displaystyle\sum_{i=m}^{n}(-1)i\displaystyle\binom{n}{m}\binom{n - m}{i - m}$(三项式系数恒等式) $= \displaystyle\binom{n}{m}\displaystyle\sum_{i=m}^{n}(-1)i\displaystyle\binom{n - m}{i - m}$($\displaystyle\binom{n}{m}$与$i$无关，可以提出) $= \displaystyle\binom{n}{m}\displaystyle\sum_{i=m}^{n}(-1)i\displaystyle\frac{(n - m)^{\displaystyle\underline{\displaystyle{i - m}}}}{(i - m)!}$(组合数展开) $=\displaystyle\binom{n}{m}\displaystyle\sum_{i=m}^{n}(-1)m\displaystyle\frac{(i - n - 1)^{\underline{i - m}}}{(i - m)!}$(上指标反转) $= (-1)^{m\displaystyle\binom{n}{m}\displaystyle\sum_{i=m}}\displaystyle\binom{i - n - 1}{m - n - 1}$(组合数的定义) $= (-1)^m\displaystyle\binom{n}{m}\displaystyle\binom{0}{m - n} = \left{
\begin{array}{lr}
(-1)^{m} & : m = n\
0 & : m \neq n
\end{array}
\right.$

例题二

有标号连通图计数，$n \leq 10^3$

分析：记$f_i$表示大小为$i$的有标号连通图的个数，$g_i$表示大小为$i$的有标号图的个数，则$g_i = 2^{\binom{n}{2}}$。考虑简单容斥，求大小为$i$i 的有标号不连通图的个数：假设$1$号点所在连通块大小为$j(j ＜ i)$，则有$f_i = g_i -\displaystyle\sum_{j = 1}^{i - 1}\displaystyle\binom{i - 1}{j - 1}f_j$

$O(n^2)$ dp即可。

例题三

一句话题意：给定$L$，$T$次询问，每次给定$n, m, k$，求：$\displaystyle\sum_{i=0}^k\displaystyle\binom{m}{i}\binom{n - m}{k - i}i^L$

$T \leq 200, n, m, k \leq 2 \times 10^7, L \leq 2 \times 10^5$

分析：原式 $= \displaystyle\sum_{i=0}^k\displaystyle\binom{m}{i}\binom{n - m}{k - i}\displaystyle\sum_{j=0}^L\Large{_jL}i^{\underline{j}}$(斯特林数的计算式) $= \displaystyle\sum_{i=0}^k\displaystyle\binom{m}{i}\binom{n - m}{k - i}\displaystyle\sum_{j=0}^L\Large{_jL}\normalsize\binom{i}{j}j!$(组合数的计算式) $= \displaystyle\sum_{j=0}^{L\displaystyle\sum_{i=0}}kj!\Large{j^L}\normalsize\binom{m}{i}\binom{i}{j}\binom{n - m}{k - i}$(将求和移动到最外层) $= \displaystyle\sum^{L\displaystyle\sum_{i=0}}kj!\Large{j^L}\normalsize\binom{m}{j}\displaystyle\binom{m - j}{i - j}\displaystyle\binom{n - m}{k - i}$(三项式系数恒等式
) $= \displaystyle\sum^Lj!\Large{_jL}\normalsize\binom{m}{j}\displaystyle\sum_{i=0}^k\displaystyle\binom{m - j}{i - j}\displaystyle\binom{n - m}{k - i}$(将只与$j$有关的因式外移) $= \displaystyle\sum_{j=0}^Lj!\Large{_jL}\normalsize\binom{m}{j}\displaystyle\binom{n - j}{k - j}$

预处理一下斯特林数和组合数就可以$O(L)$每次询问了。

10.Lucas 定理

$\displaystyle\binom{n}{m} \equiv \displaystyle\binom{\lfloor\displaystyle\frac{n}{p}\rfloor}{\lfloor\displaystyle\frac{m}{p}\rfloor}\displaystyle\binom{\displaystyle\text{n mod p} }{\displaystyle\text{m mod p}}(\displaystyle\text{mod p})$

证：①$\because\displaystyle\binom{p}{m} \text{mod p} = [m = 1 \vee m = p]$

$\therefore (a + b)^p \equiv a^p + b^p(\text{mod p})$(二项式定理展开);

$\displaystyle\binom{n}{m} = [x^m](1 + x)^n$($[xi]$表示多项式中$x^i$项的系数，由二次项定理可得)

$\therefore (1 + x)^n = (1 + x^{p\lfloor\frac{n}{p}\rfloor})(1 + x)^{n\text{ mod }p}$

$\because (1 + x^{p\lfloor\frac{n}{p}\rfloor}) \equiv (1 + x^p)\rfloor}}(\text{mod }p)$只有产生$p$倍数处的贡献，而
$(1 + x)^{n\text{ mod }p}$只在$0 \longrightarrow p - 1$处产生贡献，所以每个位置刚好被贡献一次。

②对于素数$m, r \in (0, m)$

$\displaystyle\binom{m}{r} = \displaystyle\frac{m!}{r!(m - r)!} = \displaystyle\frac{(m - 1)!}{(r - 1)!(m - r)!} \times \displaystyle\frac{m}{r} = \displaystyle\binom{m - 1}{r - 1} \times \displaystyle\frac{m}{r} \equiv 0(\text{mod }m)$

带入二项式定理的展开式，得：

$(1 + x)^m = \displaystyle\sum_{r = 0}^{m\displaystyle\binom{m}{r}x}r = 1 + \displaystyle\sum_{r=1}^{m - 1}\displaystyle\binom{m}{r}x^r + x^m \equiv 1 + x^m (\text{mod } m)$

令$n = sm + a$，有：

$(1 + x)^n = (1 + x)^{sm + a} = (1 + x)^{sm}(1 + x)^a \equiv(1 + x^m)s(1 + x)^a \equiv (\displaystyle\sum_{i=0}^{s\displaystyle\binom{s}{i}x})(\displaystyle\sum_{j=0}^{a\displaystyle\binom{a}{j}x}j) (\text{mod } m)$

又根据二项式定理$(1 + x)^n = \displaystyle\sum_{r=0}^{n\displaystyle\binom{n}{r}x}r$，与上式对比得：

$\displaystyle\sum_{r=0}^{n\displaystyle\binom{n}{r}x}r \equiv (\displaystyle\sum_{i=0}^{s\displaystyle\binom{s}{i}x})(\displaystyle\sum_{j=0}^{a\displaystyle\binom{a}{j}x}j) (\text{mod } m)$

对比两边第$x^r$次项的系数，根据$r = im + j, i = r / m, j = r \text{ mod } m, a = n \text{ mod } m, s = n / m$，得：

$\displaystyle\binom{n}{r} \equiv \displaystyle\binom{i}{s}\displaystyle\binom{j}{a} (\text{mod m}) \equiv \displaystyle\binom{\lfloor\displaystyle\frac{r}{m}\rfloor}{\lfloor\displaystyle\frac{n}{m}\rfloor}\displaystyle\binom{\displaystyle\text{r mod m} }{\displaystyle\text{n mod m}}(\displaystyle\text{mod m})$

二、二项式定理

11.二项式定理

$(x + y)^n = \displaystyle\sum_{i=0}^{{n}\displaystyle\binom{n}{i}x}y^i$

证：第$i$项的系数等于从$n$个$x + y$中选出$i$相乘后最高项系数和

练习四|牛顿级数

记$\triangle^{na$表示数列$a$差分$n$次后的数列，证明：$\triangle}na_i=\displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j}a_{i-j}$

证：①：当差分一次时，式子成立；假设对于前$n$次差分，都有$\triangle^na_i = \displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j}a_{i-j}$，则$\triangle^{n + 1}a_{i} =\displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j}a_{i-j} - \displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j - 1}a_{i-1-j} = \displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j}a_{i-j} + \displaystyle\sum_{j=1}^{n + 1}(-1)^j\displaystyle\binom{n}{j - 1}a_{i-j} = \displaystyle\sum_{j=1}^{n + 1}(-1)^j[\displaystyle\binom{n}{j}+\displaystyle\binom{n}{j - 1}]a_{i-j} = \displaystyle\sum_{j=1}^{n + 1}(-1)^j\displaystyle\binom{n + 1}{j}a_{i-j}$

符合数学归纳法，等式成立

②设$I_{a_i} = a_i, E_{a_i} = a_{i-1}$

则$\triangle^na_i = (I - E)^n = \displaystyle\sum_{j=0}^{n\displaystyle\binom{n}{j}I}(-E^j) = \displaystyle\sum_{j=0}^{n\displaystyle\binom{n}{j}(-E}j)$($I$变换多少次都不会影响序列) $= \displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j}E^j$(将$-1$提出) $= \displaystyle\sum_{j=0}^n(-1)j\displaystyle\binom{n}{j}a_{i-j}$($E^j$相当于将$a_i$左移$j$位，到$a_{i-j}$)

三、错排

12.错排

记$f_n$表示长度为$n$的，且不存在$p_i = i$的排列的个数

则$f_n = (n - 1)(f_{n - 1} + f_{n - 2})$

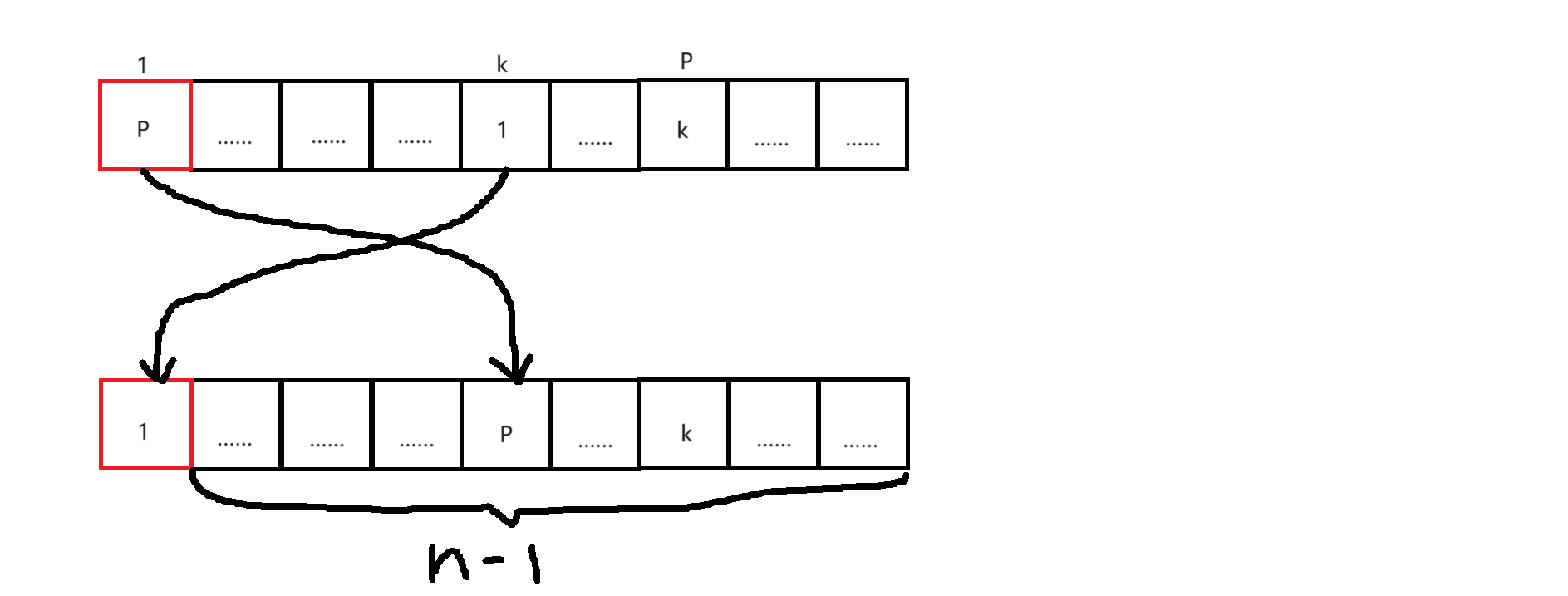
证：考虑数字$1$有$n - 1$种放法，假如放到了位置$k$，那位置$k$处的数字有两种类型的放法：要么放在位置$1$，那么剩下物品的放法就有$f_{n - 2}$种

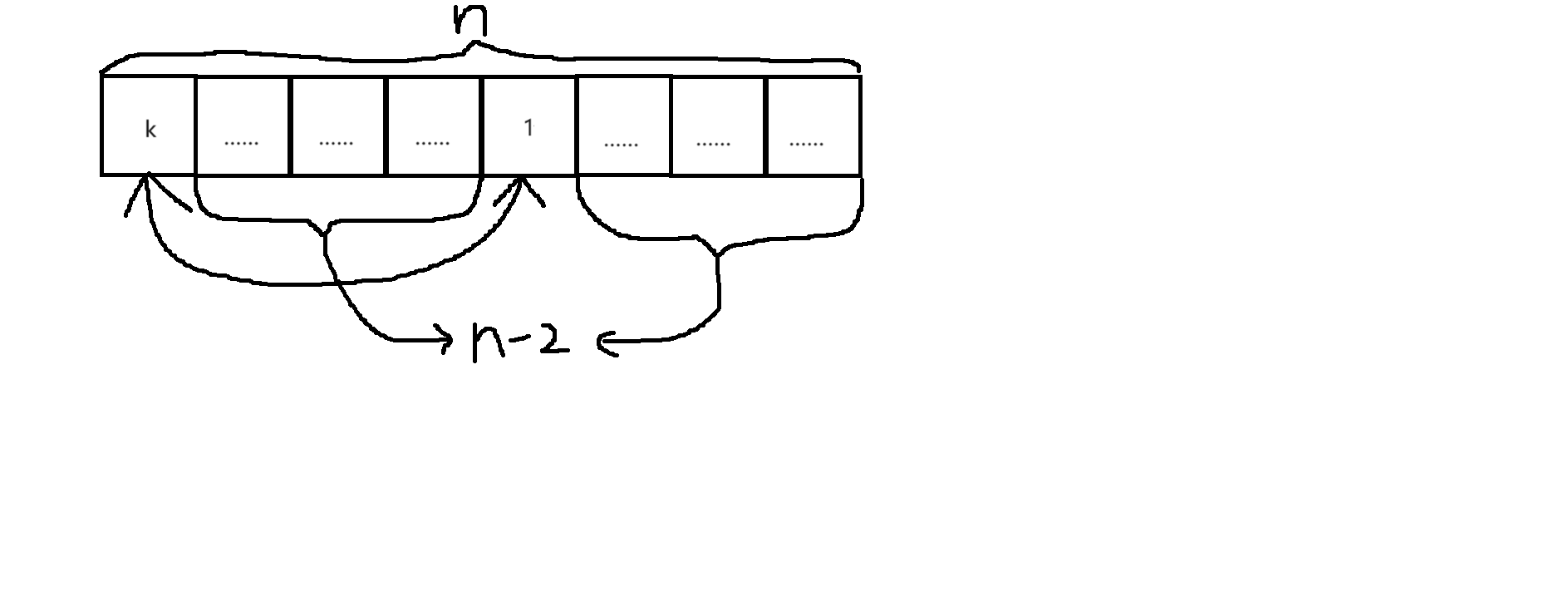
要么放在除$1$外的其他位置，那么让最后排完了时排在$1$位置的数字与排在$k$位置的数字$1$交换，不看$1$位置，就得到了一个大小为$n - 1$的错排，也就是这种情况下的每种方案可以与大小为$n - 1$的错排一一对应，故这种情况
有$f_{n - 1}$种方案。

例题四

一句话题意：记$cyc_{\pi}$表示将排列$\pi$看成置换，其中循环的个数。给定$n, k$和一个$k - 1$次多项式$F$，对于所有$1 \leq n \leq m$求$\displaystyle\sum_{\pi}F(cyc_{\pi})$

其中$\pi$表示长度为$m$的错排

$n \leq 6 \times 10^5, k \leq 100$，对$998244353$取模

分析：原式 $= \displaystyle\sum_{\pi}\displaystyle\sum_{i=0}^{k - 1}f_icyc_{\pi}^i$(将多项式展开) $= \displaystyle\sum_{\pi}\displaystyle\sum_{i=0}^{k - 1}f_i\displaystyle\sum_{j=0}^i\Large{_{j}i}\normalsize\binom{cyc_{\pi}}{j}j!$(斯特林数的计算式) $= \displaystyle\sum_{\pi}\displaystyle\sum_{i=0}^{k - 1}\displaystyle\sum_{j=0}^{if_i\Large{_{j}}i}\normalsize\binom{cyc_{\pi}}{j}j!$(将求和移动到最外层) $= \displaystyle\sum_{\pi}\displaystyle\sum_{j=0}^{k - 1}\displaystyle\sum_{i=j}^{k - 1}f_i\Large{{j}^i}\normalsize\binom{cyc{\pi}}{j}j!$(交换求和顺序) $= \displaystyle\sum_{\pi}\displaystyle\sum_{j=0}^{k - 1}\displaystyle\binom{cyc_{\pi}}{j}j!\displaystyle\sum_{i=j}^{k - 1}f_i\Large{{j}^i}$(将只与$j$有关的因式外移) $= \displaystyle\sum^{k - 1}j!\displaystyle\sum_{\pi}\displaystyle\binom{cyc_{\pi}}{j}\displaystyle\sum_{i=j}^{k - 1}f_i\Large{_{j}^i}$(将只与$\pi$有关的因式内移)

其中$\displaystyle\sum_{i=j}^{k - 1}f_i\Large{_{j}^{i}$可以$O(k}2)$预处理

记$C_{t, i}$表示有$i$个循环，长度为$t$的错排数

则$C_{t, i} = (t - 1)(C_{t - 2, i - 1} + C_{t - 1, i})$(与错排递推式推导类似)

记$P_{t, i} = \displaystyle\sum_{|\pi|=t}\displaystyle\binom{cyc_{\pi}}{i}$

考虑枚举循环个数，当循环个数为$j$时，有$C_{t, j}$种排法，每种排法对$P_{t, i}$的贡献为$\displaystyle\binom{j}{i}$

则$P_{t, i} = \displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i}C_{t, j} = \displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i}[(t - 1)(C_{t - 2, j - 1} + C_{t - 1, j})] = (t - 1)\displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i}(C_{t - 2, j - 1} + C_{t - 1, j})$(将常量外移) $= (t - 1)\displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i}C_{t - 2, j - 1} + (t - 1)\displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i} C_{t - 1, j}$(拆括号) $= (t - 1)\displaystyle\sum_{j=1}^t(\displaystyle\binom{j - 1}{i} + \displaystyle\binom{j - 1}{i - 1})C_{t - 2, j - 1} + (t - 1)\displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i} C_{t - 1, j}$(组合数递推式逆用) $= (t - 1)\displaystyle\sum_{j=1}^t\displaystyle\binom{j - 1}{i}C_{t - 2, j - 1} + \displaystyle\binom{j - 1}{i - 1}C_{t - 2, j - 1} + (t - 1)\displaystyle\sum_{j=1}^t\displaystyle\binom{j}{i} C_{t - 1, j} = (t - 1)(P_{t - 2, i} + P_{t - 2, i - 1} + P_{t - 1, i})$

于是$O(nk + k^2)$预处理一下之后，对于每个$m$，$O(k)$求答案即可。