标签：直线 AC 8.6 dfrac sqrt 垂直 qquad 平面

$\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }$【高分突破系列】高一数学下学期同步知识点剖析精品讲义！
$\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}$

必修第二册同步拔高，难度3颗星！

模块导图

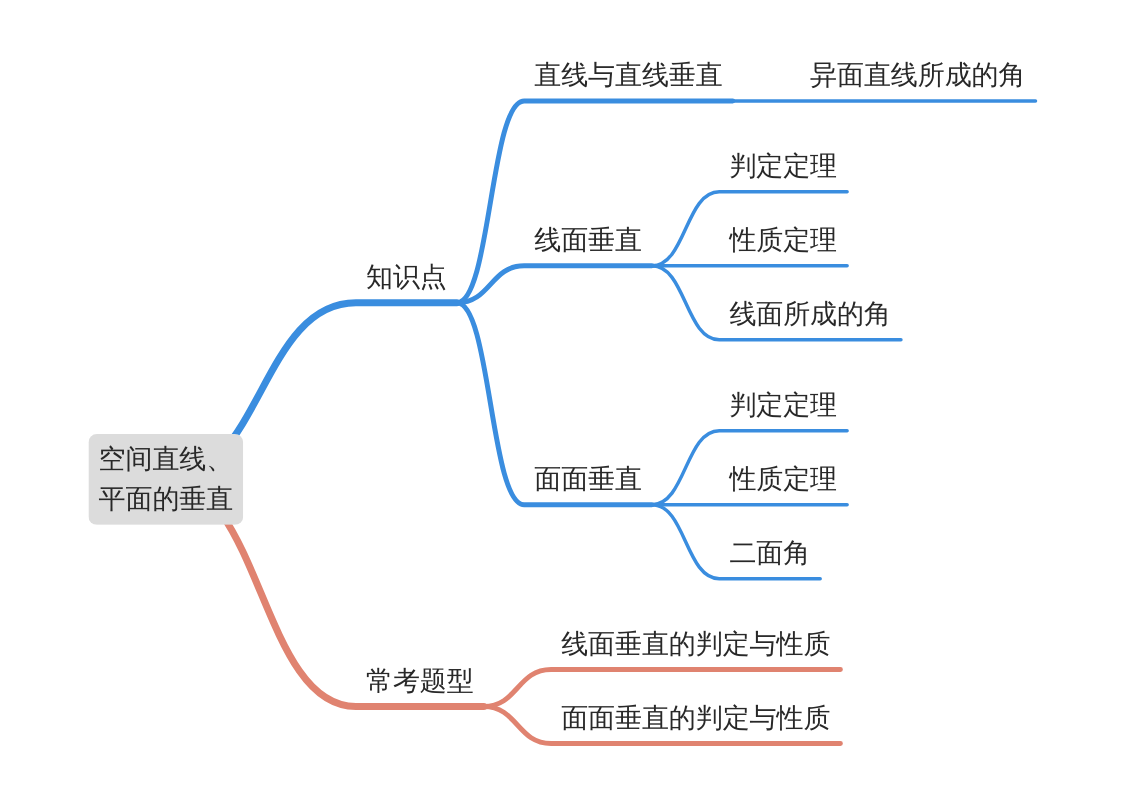
知识剖析

线线垂直

1 异面直线所成的角
(i) 范围:$θ∈[0^∘，90^∘]$；
(ii) 作异面直线所成的角:平移法.
如图，在空间任取一点$O$，过$O$作$a^{\prime} / / a$，$b^{\prime} / / b$，则$a^{\prime}， b^{\prime}$ 所成的$θ$ 角为异面直线$a，b$所成的角.特别地，找异面直线所成的角时，经常把一条异面直线平移到另
一条异面直线的特殊点(如线段中点，端点等)上，形成异面直线所成的角.

2 线线垂直
如果两条异面直线所成的角是直角，那么我们就说两条异面直线相互垂直.

线面垂直

1 定义
若一条直线垂直于平面内的任意一条直线，则这条直线垂直于平面.
符号表述:若任意$a⊂α$都有$l⊥a$，则$l⊥α$.

2 判定定理
如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直.
$\left.\begin{array}{c} a， b \subset \alpha \\ a \cap b=0 \\ l \perp a \\ l \perp b \end{array}\right\} \Rightarrow l \perp \alpha$ (线线垂直⇒线面垂直)

3 性质
$(i) l⊥α，a⊂α⇒ l⊥ a$ (线面垂直⇒线线垂直)
$(ii)$ 垂直同一平面的两直线平行 $a⊥α$，$b⊥α⇒ a // b$.

4 证明线面垂直的方法
方法1 定义法(反证)
方法2 判定定理(常用)
方法3 $\left.\begin{array}{l} a / / b \\ a \perp \alpha \end{array}\right\} \Rightarrow b \perp \alpha$
方法4 $\left.\begin{array}{c} \alpha / / \beta \\ a \perp \alpha \end{array}\right\} \Rightarrow a \perp \beta$
方法5 $\left.\begin{array}{c} \alpha \perp \beta \\ a \cap \beta=b \\ a \subset \alpha \\ a \perp b \end{array}\right\} \Rightarrow a \perp \beta$(面面垂直⇒线面垂直)

5 线面所成的角
(1) 定义
如下图，平面的一条斜线(直线l)和它在平面上的射影($AO$)所成的角，叫做这条直线和这个平面所成的角.

一条直线垂直平面，则$θ=90^°$；一条直线和平面平行或在平面内，则$θ=0^°$.

(2) 范围
直线和平面所成的角$θ$的取值范围是$0^°≤θ≤90^°$.

面面垂直

1 二面角
(1) 定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
在二面角的棱$l$上任取一点$O$，以点$O$为垂足，在半平面$α$和$β$内分别作垂直于棱l的射线$OA$和$OB$，则射线$OA$和$OB$构成的$∠AOB$叫做二面角的平面角.

(2) 范围
二面角的平面角α的取值范围是$[0^°，180^°]$.

2 面面垂直
(1) 定义
若二面角$α-l-β$的平面角为$90^∘$，则 $α⊥β$；

(2) 判定定理
如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.
$\left.\begin{array}{c} a \subset \alpha \\ a \perp \beta \end{array}\right\} \Rightarrow \alpha \perp \beta$ (线面垂直⇒面面垂直)

(3) 性质定理
两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直.
$\left.\begin{array}{c} \alpha \perp \beta \\ \alpha \cap \beta=A B \\ a \subset \alpha \\ a \perp A B \end{array}\right\} \Rightarrow a \perp \beta$ (面面垂直⇒线面垂直)
判断
(1) 如果平面$α⊥$平面$γ$，平面$β⊥$平面$γ$，$α∩β=l$，那么$l⊥γ$ ( √ )
(2) 如果平面$α⊥$平面$β$，那么平面$α$内一定存在直线平行于平面$β$ ( √ )
(3) 如果平面$α⊥$平面$β$，过$α$内任意一点作交线的垂线，那么此垂线必垂直于$β$ ( × )
(4) 如果平面$α$不垂直于平面$β$，那么平面$α$内一定不存在直线垂直于平面$β$ ( √ )

经典例题

【题型一】线面垂直的判定与性质

【典题1】 如图，已知$△ABC$是正三角形，$EA、CD$都垂直于平面$ABC$，且$EA=AB=2a$，$DC=a$，$F$是$BE$的中点，
求证:$(1)FD∥$平面$ABC$； $\qquad \qquad$ $(2)AF⊥$平面$EDB$

【证明】 (1) $∵F$是$BE$的中点，取$BA$的中点$M$，

$∴FM//EA$，$F M=\dfrac{1}{2} E A=a$
$∵EA、CD$都垂直于平面$ABC$，$∴CD∥EA$，
$∴CD∥FM$，又$CD=a=FM$
$∴$四边形$FMCD$是平行四边形，$∴FD∥MC$，
又$∵FD⊄$平面$ABC$，$MC⊂$平面$ABC$，$∴FD∥$平面$ABC$．
(2)因$M$是$AB$的中点，$△ABC$是正三角形，所以$CM⊥AB$
又$EA$垂直于平面$ABC$ ，
$∴CM⊥AE$
又 $AE∩AB=A$，所以$CM⊥$面$EAB$，
$∵AF⊂$面$EAB$ ， $∴CM⊥AF$
又$CM∥FD$，从而$FD⊥AF$，
因$F$是$BE$的中点，$EA=AB$，所以$AF⊥EB$．
$EB，FD$是平面$EDB$内两条相交直线，
所以$AF⊥$平面$EDB$．
【点拨】
① 线面垂直的判定：如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直；它可把线面垂直转化为线线垂直，本题中$AF⊥$平面$EDB⇒$在平面$EDB$上找到两条相交直线均垂直$AF$；
② 线面垂直的性质：$l⊥α$，$a⊂α⇒ l⊥ a$；它可由线面垂直得到线线垂直；
③ 等腰三角形要注意“三线合一”的运用.

【典题2】 $P$为$△ABC$所在平面外一点，$O$为$P$在平面$ABC$上的射影．

(1)若$PA、PB、PC$两两互相垂直，则$O$点是$△ABC$的 $\underline{\quad \quad}$心；
(2)若$P$到$△ABC$三边距离相等，且$O$在$△ABC$内部，则$O$点是$△ABC$的 $\underline{\quad \quad}$心；
(3)若$PA⊥BC$，$PB⊥AC$，$PC⊥AB$，则$O$点是$△ABC$的$\underline{\quad \quad}$ 心；
(4)若$PA、PB、PC$与底面$ABC$成等角，则$O$点是$△ABC$的$\underline{\quad \quad}$心．
【解析】 如图$P$到$△ABC$所在平面外一点，$O$是$P$点在平面$a$上的射影．
(1) 若$PA、PB、PC$两两互相垂直，由可证得$BC⊥OA$，$AB⊥OC$，$AC⊥OB$，即此时点$O$是三角形三边高的交点，故此时点$O$是三角形的垂心，故应填:垂．
(2) 若$P$到$△ABC$三边的距离相等，$E，F，D$分别是点$P$在三个边上的垂足，故可证得$OE$，$OF$，$OD$分别垂直于三边且相等，由内切圆的加心的定义知，此时点$O$是三角形的内心，故应填:内；
(3) 若$PA⊥BC$，$PB⊥AC$，因为$PO⊥$底面$ABC$，所以$AO⊥BC$，同理$BO⊥AC$，可得$O$是$△ABC$的垂心；故应填:垂．
(4) 若$PA、PB、PC$与地面$ABC$成等角，由条件可证得$OA=OB=OC$，由三角形外心的定义知此时点$O$是三角形的外心，故应填:外；
综上，三空答案依次应为垂、内、垂、外
【点拨】 三角形的四心：

【典题3】 如图，在矩形$ABCD$中，$AB=8$，$BC=4$，$E$为$DC$边的中点，沿$AE$将$△ADE$折起，在折起过程中，有几个正确(　　)
①$ED⊥$平面$ACD$ $\qquad \qquad$
②$CD⊥$平面$BED$ $\qquad \qquad$
③$BD⊥$平面$ACD$ $\qquad \qquad$
④$AD⊥$平面$BED$．

A．$1$个 $\qquad \qquad \qquad \qquad$ B．$2$个 $\qquad \qquad \qquad \qquad$ C．$3$个 $\qquad \qquad \qquad \qquad$ D．$4$个
【解析】 $∵$在矩形$ABCD$中，$AB=8$，$BC=4$，$E$为$DC$边的中点，
$∴$设$D$点在平面$BCE$上的投影为$Q$，在折起过程中，点$Q$的轨迹为下图$Q_1$到$Q_2$的四分之一圆．

此过程中始终有$DQ⊥$平面$AECB$
对于① 假设$ED⊥$平面$ACD$，则$ED⊥AC$，
又$∵DQ⊥AC$，则$AC⊥$平面$DEQ$$⇒QE⊥AC$，
但由图可知$QE$不可能垂直$AC$，产生了矛盾，故假设不成立，故①错误；

对于② 假设$CD⊥$平面$BED$，则$CD⊥BE$，
又$∵DQ⊥BE$，则$BE⊥$平面$CDQ$$⇒BE⊥CQ$，
但由图可知只有$D$点投影位于$Q_2$位置时，才有$BE⊥CQ$，此时$CD⊂$平面$BED$，显然不能满足$CD⊥$平面$BED$，产生了矛盾，故假设不成立，故②错误；

对于③ 假设$BD⊥$平面$ACD$，则$BD⊥AC$，
又$∵DQ⊥AC$，则$AC⊥$平面$BDQ$$⇒AC⊥BQ$，
但由图可知$BQ$不可能垂直$AC$，产生了矛盾，故假设不成立，故③错误；

对于④ $∵AD⊥ED$，$∴$若要满足$AD⊥$平面$BED$，则只需要$AD⊥EB$，而$DQ⊥EB$，若$AQ⊥EB$便可，在折叠的过程中易得存在一个位置使得$AQ⊥EB$($Q$为弧线$Q_1 Q_2$与线段$AE$的交点)，故④正确．

故选:$A$
【点拨】
① 对于①--③，均利用了反证法进行否决；
② 在对于运动变化的题目，一定要明确哪些量是不变的，哪些量是变化的！

【题型二】面面垂直的判定与性质

【典题1】 如图，已知四棱锥$P－ABCD$中，已知$PA⊥$底面$ABCD$，且底面$ABCD$为矩形，则下列结论中错误的是（　　）

A．平面$PAB⊥$平面$PAD$ $\qquad \qquad \qquad \qquad$ B．平面$PAB⊥$平面$PBC$
C．平面$PBC⊥$平面$PCD$ $\qquad \qquad \qquad \qquad$ D．平面$PCD⊥$平面$PAD$
【解析】
方法一
对于$A$，因为已知$PA⊥$底面$ABCD$，且底面$ABCD$为矩形，
所以$PA⊥AB$，又$AB⊥AD$，$AB⊥$平面$PAD$，
所以平面$PAB⊥$平面$PAD$，故$A$正确；
对于$B$，已知$PA⊥$底面$ABCD$，且底面$ABCD$为矩形，
所以$PA⊥BC$，又$BC⊥AB$，所以$BC⊥$平面$PAB$，
所以平面$PAB⊥$平面$PBC$，故$B$正确；
对于$D$，已知$PA⊥$底面$ABCD$，且底面$ABCD$为矩形，
所以$PA⊥CD$，又$CD⊥AD$，
所以$CD⊥$平面$PAD$，所以平面$PCD⊥$平面$PAD$，故$D$正确；
故选$C$．
方法二
$∵PA⊥$底面$ABCD$，且底面$ABCD$为矩形，
$∴$四棱锥$P－ABCD$可视为正方体的一部分，如下图，

根据正方形的特性，$∵$平面$PCD⊥$平面$BCC_1 B_1$，
$∴$平面$PBC⊥$平面$PCD$是不可能的，
容易选出$C$.
【点拨】
① 面面垂直的判定定理：两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直.它可以把面面垂直转化为线面垂直或线线垂直；
② 方法二比较巧妙，通过构造正方体进行求解.

【典题2】 如图，直角$△ABC$中，$∠ACB=90°$，$BC=2AC=4$，$D$、$E$分别是$AB$、$BC$边的中点，沿$DE$将$△BDE$折起至$△FDE$，且$∠CEF=60°$．
(1)求四棱锥$F－ADEC$的体积； $\qquad \qquad$ (2)求证:平面$ADF⊥$平面$ACF$．

【解析】 (1)$D$、$E$分别是$AB$、$BC$边的中点，
$∴DE$平行且等于$AC$的一半，$DE⊥BC$，$DE=1$
依题意，$DE⊥EF$，$BE=EF=2$，
$∵EF∩EC=E$，$∴DE⊥$平面$CEF$，
又$∵DE⊂$平面$ACED$，
$∴$平面$ACED⊥$平面$CEF$
作$FM⊥EC$于$M$，则$FM⊥$平面$ACED$，
$∵∠CEF=60°$，$\therefore F M=\sqrt{3}$
梯形$ACED$的面积$S=\dfrac{1}{2}(A C+E D) \times E C=\dfrac{1}{2}(1+2) \times 2=3$
四棱锥$F－ADEC$的体积$V=\dfrac{1}{3} S h=\dfrac{1}{3} \times 3 \times \sqrt{3}=\sqrt{3}$
(2)方法1
如图2．取线段$AF$、$CF$的中点$N$、$Q$，连接$DN$、$NQ$、$EQ$，
则$NQ$平行且等于$AC$的一半，
$∴NQ$平行且等于$DE$，$DEQN$是平行四边形，$∴DN∥EQ$
$∵EC=EF$，$∠CEF=60°$，
$∴△CEF$是等边三角形，$EQ⊥FC$，
又$∵DE⊥$平面$CEF$，$DE⊥EQ$，$∴AC⊥EQ$，
$∵FC∩AC=C$，$∴EQ⊥$平面$ACF$ $∴DN⊥$平面$ACF$，
又$DN⊂$平面$ADF$，$∴$平面$ADF⊥$平面$ACF$
方法2 连接$BF$，$∵EC=EF$，$∠CEF=60°$，
$∴△CEF$是边长为$2$等边三角形
$∵BE=EF，$$\therefore \angle E B F=\dfrac{1}{2} \angle C E F=30^{\circ}$，
$∴∠BFC=90°$，$BF⊥FC$
$DE⊥$平面$BCF$，$DE∥AC$，
$∴AC⊥$平面$BCF$
$∵BF⊂$平面$BCF$，$∴AC⊥BF$，又$∵FC∩AC=C$，
$∴BF⊥$平面$ACF$，
又$∵BF⊂$平面$ADF$，$∴$平面$ADF⊥$平面$ACF$

【点拨】
① 面面垂直的性质定理：两个平面垂直，如果一个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直.它利用面面垂直证明线面垂直；
② 线线垂直、线面垂直、面面垂直之间的转化

③ 确定高的时候，要证明出它垂直底面才行(即$FM⊥$平面$ACED$，$FM$才是高).

【典题3】 长方形$ABCD$中，$AB=2$，$BC=1$，$F$是线段$DC$上一动点，且$0<FC<1$．将$△AFD$沿$AF$折起，使平面$AFD⊥$平面$ABC$，在平面$ABD$内作$DK⊥AB$于$K$，设$AK=t$，则$t$的值可能为(　　)

A. $\dfrac{4}{3}$ $\qquad \qquad \qquad \qquad$ B. $\dfrac{3}{4}$ $\qquad \qquad \qquad \qquad$ C. $ \dfrac{1}{3}$ $\qquad \qquad \qquad \qquad$ D. $\dfrac{1}{4}$
【解析】 如图，过$D$作$DG⊥AF$，垂足为$G$，连接$GK$，

$∵$平面$AFD⊥$平面$ABC$，
又$DK⊥AB$，$∴AB⊥$平面$DKG$，$∴AB⊥GK$．
方法一把折叠后几何体展开为平面图形，如下图，

设$DF=x$，
$∵0<FC<1$，$∴1<x<2$；
在$Rt△ADF$中，$A F=\sqrt{1+x^{2}}$；
由对$Rt△ADF$利用等积法，
可得$\dfrac{D G \times A F}{2}=\dfrac{A D \times D F}{2} \Rightarrow D G=\dfrac{x}{\sqrt{1+x^{2}}}$；
在$Rt△ADG$中，$A G=\sqrt{A D^{2}-D G^{2}}=\dfrac{1}{\sqrt{1+x^{2}}}$；
$∵Rt△ADG∼Rt△AGK$，
$\therefore \dfrac{A K}{A G}=\dfrac{D G}{A D} \Rightarrow A K=\dfrac{x}{1+x^{2}}$，即$t=\dfrac{x}{1+x^{2}}=\dfrac{1}{x+\dfrac{1}{x}}$
$∵1<x<2$ 由对勾函数$f(x)=x+\dfrac{1}{x}$可知$2<x+\dfrac{1}{x}<\dfrac{5}{2}$
则$\dfrac{2}{5}<\dfrac{1}{x+\dfrac{1}{x}}<\dfrac{1}{2}$，即$t$的取值范围是$\left(\dfrac{2}{5}， \dfrac{1}{2}\right)$.
方法二把折叠后几何体展开为平面图形，如下图，

设$∠DAG=α$，则$∠AGK=α$，
易得$A G=A D \times \cos \alpha=\cos \alpha$，$A K=A G \times \sin \alpha=\cos \alpha \cdot \sin \alpha=\dfrac{\sin 2 \alpha}{2}$，即$t=\dfrac{\sin 2 \alpha}{2}$，
当$FC=1$时，$F$为$CD$的中点，此时$\alpha=\dfrac{\pi}{4}$；
当$FC=0$时，$F$与$C$重合，此时设$α=β$，其中$\sin \beta=\dfrac{2 \sqrt{5}}{5}$；
即当$0<FC<1$时，$\alpha \in\left(\dfrac{\pi}{4}， \beta\right)$，$\therefore 2 \alpha \in\left(\dfrac{\pi}{2}， 2 \beta\right)$
$∵y=\sin x$在$\left(\dfrac{\pi}{2}， 2 \beta\right)$上递减，
$\therefore \dfrac{2}{5}=\sin 2 \beta<\dfrac{\sin 2 \alpha}{2}<\dfrac{1}{2} \times \sin \dfrac{\pi}{2}=\dfrac{1}{2}$
故$t$的取值范围是$\left(\dfrac{2}{5}， \dfrac{1}{2}\right)$
故选：$B$．
【点拨】
① 对于处于变化的题目中，要注意几点：
(1) 哪些是变量，哪些是恒量(恒量：线段$AD=1$，$AD⊥DF$等；变量：线段$DF$，角$∠DAG$等)；
(2) 明确在变量中，某个变量是由哪个变量而引起变化的，“源头的变量”在哪里；比如在方法二中，$DG$是变量，可以说它是随角$∠DAG$变化，而角$∠DAG$是随线段$DF$变化，线段$DF$随线段$CF$变化，显然变量线段$CF$是本题的“源头的变量”；
(3) 明确相关变量之间是怎么变化的，显然线段$DF$是随线段$CF$增大而递减的，在方法一中可知线段$A K=t=\dfrac{1}{x+\frac{1}{x}}$是随线段$DF=x$的增大而递减的；
② ”明确相关变量之间是怎么变化”这点，本题要求$AK=t$的范围，显然它由线段$CF$变化的，但方法一中$A K=t=\dfrac{x}{1+x^{2}}$(其中$DF=x$)，方法二中$A K=t=\dfrac{\sin 2 \alpha}{2}$(其中角$∠DAG=α$)，选择哪个变量作为函数的自变量，主要看函数的表达是否简便、计算量是否够小，不会以线段$CF$为自变量，显然方法二会更好些.
③ 求变量的取值范围，多利用函数的单调性求解，此时要注意自变量的取值范围，函数思想无处不在；
④ 本题中变量之间的关系通过平面几何的知识点得到，其中相似三角形、等积法、勾股定理、三角函数等基础知识点常常用到.

巩固练习

1(★★) 如图：$PA⊥⊙O$所在的平面，$AB$是$⊙O$的直径，$C$是$⊙O$上的一点，$AE⊥PC$，$AF⊥PB$，给出下列结论①$AE⊥BC$，②$AE⊥PB$，③$AF⊥BC$，④$AE⊥$平面$PBC$，其中正确命题的序号是 (　　)

A. $(1) (2)$ $\qquad \qquad \qquad \qquad$ B. $ (1) (3) $ $\qquad \qquad \qquad \qquad$ C. $ (1)(2)(4) $ $\qquad \qquad \qquad \qquad$ D. $ (1) (3)$

2(★★) $PA$垂直于正方形$ABCD$所在平面，连接$PB$，$PC$，$PD$，$AC$，$BD$，则下列垂直关系正确的是（　　）
①面$PAB⊥$面$PBC$ $\qquad \qquad$ ②面$PAB⊥$面$PAD$
③面$PAB⊥$面$PCD$ $\qquad \qquad$ ④面$PAB⊥$面$PAC$．

A. $(1)(2) $ $\qquad \qquad \qquad \qquad$ B. $ (1)(3)$ $\qquad \qquad \qquad \qquad$ C. $ (2)(3)$ $\qquad \qquad \qquad \qquad$ D. $ (2) (4)$

3(★★) 已知边长为$a$的正$△ABC$的中线$AF$与中位线$DE$相交于点$G$，现将$△AED$沿$DE$翻折为$△A'ED$，如图是翻折过程中的一个图形，则下列四个结论：
①动直线$A'F$与直线$DE$互相垂直；
②恒有平面$A'GF⊥$平面$BCED$；
③四棱锥$A'－BCED$的体积有最大值；
④三棱锥$A'－DEF$的侧面积没有最大值．
其中正确结论的个数是（　　）

A．$1$ $\qquad \qquad \qquad \qquad$ B．$2$ $\qquad \qquad \qquad \qquad$ C．$3$ $\qquad \qquad \qquad \qquad$ D．$4$

4(★★) 如图所示，三棱锥$P－ABC$的底面在平面$α$内，且$AC⊥PC$，平面$PAC⊥$平面$PBC$，点$P$，$A$，$B$是定点，则动点$C$的轨迹是(　　)

A．一条线段 $\qquad \qquad$ B．一条直线 $\qquad \qquad$ C．一个圆 $\qquad \qquad$ D．一个圆，但要去掉两个点

5(★★) 如图，已知平面$α⊥$平面$β$，$A、B$是平面$α$与平面$β$的交线上的两个定点，$DA⊂β$，$CB⊂β$，且$DA⊥α$，$CB⊥α$，$AD=4$，$BC=8$，$AB=6$，在平面$α$上有一个动点$P$，使得$∠APD=∠BPC$，则$△PAB$的面积的最大值是(　　)

A．$24$ $\qquad \qquad \qquad \qquad$ B．$32$ $\qquad \qquad \qquad \qquad$ C．$12$ $\qquad \qquad \qquad \qquad$ D．$48$

6(★★) 如图，在长方体$ABCD－A_1 B_1 C_1 D_1$中，底面$ABCD$是正方形，$E$是$DD_1$的中点．
(1)求证：$AC⊥B_1 D$；$\qquad \qquad$ (2)若$B_1 D⊥$平面$ACE$，求$\dfrac{A A_{1}}{A B}$的值．

7(★★★) 如图，在边长为$4$的菱形$ABCD$中，$∠DAB=60°$．点$E、F$分别在边$CD、CB$上，点$E$与点$C$、$D$不重合，$EF⊥AC$，$EF∩AC=O$．沿$EF$将$△CEF$翻折到$△PEF$的位置，使平面$PEF⊥$平面$ABFED$．

(1)求证：$BD⊥$平面$POA$；
(2)当$PB$取得最小值时，求四棱锥$P－BDEF$的体积．

8(★★★) 如图，四棱锥$S－ABCD$的底面是正方形，侧棱$SA⊥$底面$ABCD$，过$A$作$AE$垂直$SB$交$SB$于$E$点，作$AH$垂直$SD$交$SD$于$H$点，平面$AEH$交$SC$于$K$点，$P$是$SA$上的动点，且$AB=1$，$SA=2$．
(1)试证明不论点$P$在何位置，都有$DB⊥PC$；
(2)求$PB+PH$的最小值；
(3)设平面$AEKH$与平面$ABCD$的交线为$l$，求证：$BD∥l$．

参考答案

【答案】 $C$
【解析】 $∵AB$是$⊙O$的直径，$∴AC⊥BC$，
$∵PA⊥⊙O$所在平面，
$∴PA⊥AC$，$PA⊥AB$，$PA⊥BC$，
$∴BC⊥$面$PAC$，$∴BC⊥AE$，
$∴AE⊥PC$，
$∵BC∩PC=C$，
$∴AE⊥$面$PBC$，∴④正确；
$∵BC，PB⊂$面$PBC$，$∴AE⊥BC$，$AE⊥PB$，
$∴$①②正确；
若$AF⊥BC$，则$AF⊥$面$PBC$，
此时$E，F$重合，与已知矛盾．$∴$③错误；
故①②④正确．
故选$C$．
【证明】 由于$BC⊥AB$，由$PA$垂直于正方形$ABCD$所在平面，所以$BC⊥PA$，易证$BC⊥$平面$PAB$，则平面$PAB⊥$平面$PBC$；又$AD∥BC$，故$AD⊥$平面$PAB$，则平面$PAD⊥$平面$PAB$．
故选$A$．
【答案】 $C$
【解析】 因为已知边长为$a$的正$△ABC$的中线$AF$与中位线$DE$相交于点$G$，所以$DE⊥AG$，$DE⊥A′G$，所以$DE⊥$平面$A′FG$，
所以$DE⊥A′F$；故①正确；
②由①得$DE⊂$平面$BCED$，所以平面$A′GF⊥$平面$BCED$；故②正确；
③三棱锥$A′－FED$的底面积是定值，体积由高即$A′$到底面的距离决定，当平面$A′DE⊥$平面$BCED$时，三棱锥$A′－FED$的体积有最大值，故③正确；
故选$C$．
【答案】 $D$
【解析】 $∵$平面$PAC⊥$平面$PBC$，
而平面$PAC∩$平面$PBC=PC$，
又$AC⊂$面$PAC$，且$AC⊥PC$，$∴AC⊥$面$PBC$，
而$BC⊂$面$PBC$，$∴AC⊥BC$，
$∴$点$C$在以$AB$为直径的圆上，
$∴$点$C$的轨迹是一个圆，但是要去掉$A$和$B$两点．
故选：$D$．
【答案】 $C$
【解析】 由题意平面$α⊥$平面$β$，$A、B$是平面$α$与平面$β$的交线上的两个定点，$DA⊂β$，$CB⊂β$，且$DA⊥α$，$CB⊥α$，
$∴△PAD$与$△PBC$是直角三角形，又$∠APD=∠BPC$，
$∴△PAD∽△PBC$，又$AD=4$，$BC=8$，
$∴PB=2PA$
如图，

作$PM⊥AB$，垂足为$M$，令$AM=t$，
在两个$Rt△PAM$与$Rt△PBM$中，$AM$是公共边及$PB=2PA$
$\therefore P A^{2}-t^{2}=4 P A^{2}-(6-t)^{2}$，解得$P A^{2}=12-4 t$
$\therefore P M=\sqrt{12-4 t-t^{2}}$．
$\therefore S =\dfrac{1}{2} \times AB \times PM =\dfrac{1}{2} \times 6 \times \sqrt{12-4 t-t^{2}}$$=3 \sqrt{12-4 t-t^{2}}=3 \sqrt{16-(t+2)^{2}} \leq 12$．
即三角形面积的最大值为$12$．
【答案】 （1）见解析（2）$\sqrt{2}$
【解析】 (1)证明：连接$BD$
$∵$底面$ABCD$是正方形，$∴AC⊥BD$
又$∵$在长方体$A B C D-A_{1} B_{1} C_{1} D_{1}$中，$\therefore B_{1} B \perp$面$ABCD$
$\therefore B_{1} B \perp A C$
又因为$B D \cap B_{1} B=B$，所以$AC⊥$面$B_{1} B D$
又$\because B_{1} D \subset$面$B_{1} B D$，$\therefore A C \perp B_{1} D$
(2)连接$D C_{1}$，$D C_{1}$是$B_{1} D$在平面$C C_{1} D_{1} D$上的射影
$\because B_{1} D \perp$平面$ACE$且$CE⊂$平面$ACE$，$\therefore B_{1} D \perp C E$
$\because D C_{1}$是$B_{1} D$在平面$C C_{1} D_{1} D$上的射影，$∴CE⊥DC$
在平面$C C_{1} D_{1} D$中如图所示$∠C_1DC=∠CED$，

$\therefore \triangle C_{1} D C \sim \triangle C E D$，$\therefore \dfrac{C D}{C_{1} C}=\dfrac{E D}{C D}$，即$\dfrac{C D}{C_{1} C}=\dfrac{\dfrac{1}{2} C_{1} C}{C D}$
$\therefore 2 C D^{2}=C C_{1}^{2}$
$\therefore \dfrac{C_{1} C}{C D}=\sqrt{2}$，即$\dfrac{A A_{1}}{A B}=\sqrt{2}$
故$\dfrac{A A_{1}}{A B}$的值为$\sqrt{2}$．
【答案】 $(1)$见解析 $(2) 3$
【解析】 (1)证明：$∵$菱形$ABCD$的对角线互相垂直，
$∴BD⊥AC$，$∴BD⊥AO$，
$∵EF⊥AC$，$∴PO⊥EF$．
$∵$平面$PEF⊥$平面$ABFED$，平面$PEF∩$平面$ABFED=EF$，且$PO⊂$平面$PEF$，
$∴PO⊥$平面$ABFED$，
$∵BD⊂$平面$ABFED$，$∴PO⊥BD$．
$∵AO∩PO=O$，$∴BD⊥$平面$POA$．
(2)设$AO∩BD=H$．因为$∠DAB=60°$，
所以$△BDC$为等边三角形，
故$BD=4$，$HB=2$，$H C=2 \sqrt{3}$．
又设$PO=x$，则$O H=2 \sqrt{3}-x$，$O A=4 \sqrt{3}-x$．
由$OH⊥BD$，则$|O B|^{2}=(2 \sqrt{3}-x)^{2}+2^{2}$，
又由(1)知，$PO⊥$平面$BFED$，则$PO⊥OB$
所以$|P B|=\sqrt{(2 \sqrt{3}-x)^{2}+2^{2}+x^{2}}=\sqrt{2(x-\sqrt{3})^{2}+10}$，
当$x=\sqrt{3}$时，$|P B|_{\min }=\sqrt{10}$．
此时$P O=\sqrt{3}$，$E F=\dfrac{1}{2} B D=2$，$O H=\sqrt{3}$
所以$V_{\text {四棱雉P-BFED }}=\dfrac{1}{3} \cdot S_{\text {梯形BFED }} \cdot P O=\dfrac{1}{3} \cdot \dfrac{(2+4) \sqrt{3}}{2} \cdot \sqrt{3}=3$．
【答案】 （1）见解析（2）$\dfrac{\sqrt{85}}{5}$ （3）见解析
【解析】 ((1)证明：$∵$底面$ABCD$是正方形 $∴DB⊥AC$，
$∵SA⊥$底面$ABCD$，$BD⊂$面$ABCD$，$∴DB⊥SA$，
又$SA∩AC=A$ $∴BD⊥$平面$SAC$，
$∵$不论点$P$在何位置都有$PC⊂$平面$SAC$，
$∴DB⊥PC$．
(2)解：将侧面$SAB$绕侧棱$SA$旋转到与侧面$SAD$在同一平面内，如图示，

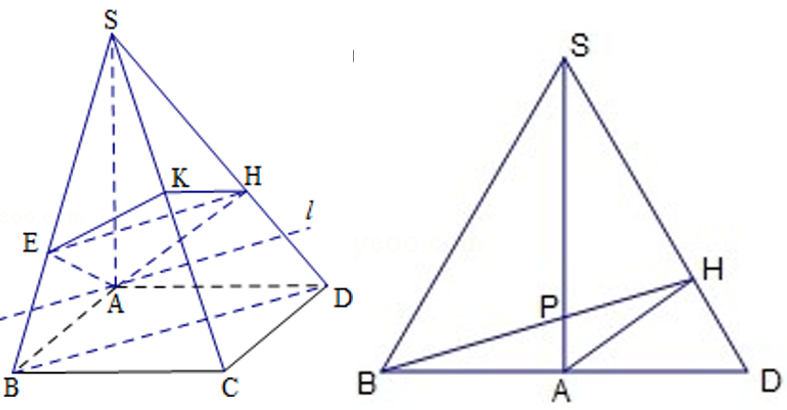
则当$B、P、H$三点共线时，$PB+PH$取最小值，
这时，$PB+PH$的最小值即线段$BH$的长，
设$∠HAD=α$，则$∠BAH=π－α$，
在$Rt△AHD$中，$\because A H=\dfrac{S A \cdot A D}{S D}=\dfrac{2}{\sqrt{5}}$，$\therefore \cos \alpha=\dfrac{A H}{A D}=\dfrac{2}{\sqrt{5}}$，
在三角形$BAH$中，有余弦定理得：
$B H^{2}=A B^{2}+A H^{2}-2 A B \cdot A H \cos (\pi-\alpha)$$=1+\dfrac{4}{5}-2 \times \dfrac{2}{\sqrt{5}} \times\left(-\dfrac{2}{\sqrt{5}}\right)=\dfrac{17}{5}$，
$\therefore(P B+P H)_{\min }=\dfrac{\sqrt{85}}{5}$．
(3)连结$EH$，$∵AB=AD$，$SA=SA$，
$∴Rt△SAB≌Rt△SAD$，
$∴SB=SD$，又$∵AE⊥SB$，$AH⊥SD$，
$∴AE=AH$，$∴Rt△SEA≌Rt△SAH$，
$∴SE=SH$，$\therefore \dfrac{S E}{S B}=\dfrac{S H}{S D}$，$∴EH∥BD$，
又$∵EH⊂$面$AEKH$，$BD⊈$面$AEKH$，$∴BD∥$面$AEKH$．
$∵$平面$AEKH∩$平面$ABCD=l$，$∴BD∥l$