\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
线线的位置关系
(1) 空间直线的位置关系
\[\left\{\begin{array}{l} \text { 共面直线 }\left\{\begin{array}{l} \text { 相交直线: 在同一平面内, 有且只有一个公共点, } a \cap b=A ; \\ \text { 平行直线:在同一平面内,没有公共点,}a|| b \end{array}\right. \\ \text { 异面直线 } \end{array}\right.\]
(2) 异面直线
① 定义:不同在任何一个平面内的两条直线;
② 图形语言

【例】 在长方体中\(ABCD-A'B'C'D'\)中,说下哪些直线相交、平行、异面么?

解 平行直线:直线\(AD\)和BC,直线\(AB\)和\(C'D'\)等;相交直线:直线\(AD\)和\(AB'\),直线\(CD\)和\(C'C\)等;
异面直线:直线\(CD\)和\(AB'\),直线\(AD\)和\(BC'\)等. (答案不唯一)
线面的位置关系
(1) 直线与平面的位置关系
\[\left\{\begin{array}{l} \text { 直线在平面内: 有无数个公共点, } m \subset \alpha \\ \text { 直线与平面相交: 有且只有一个公共点, } m \cap \alpha=A \\ \text { 直线与平面平行: 没有公共点, } m / / \alpha \end{array}\right.\]
(2) 图形语言
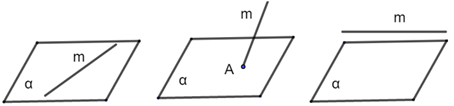
【例】在长方体中中,说下哪些直线\(CD'\)与哪些平面相交、平行、在面内?

解 直线\(CD'\)在平面\(CC'D'D\)内,与平面\(ABB'A'\)平行,与平面\(AB'C'D\)相交.(答案不唯一)
面面的位置关系
(1) 平面与平面的位置关系
\[\left\{\begin{array}{c} \text { 两个平面平行: 没有公共点, } \alpha \| \beta \\ \text { 两个平面相交: 有一条公共直线, } \alpha \cap \beta=m \end{array}\right.\]
(2) 图形语言
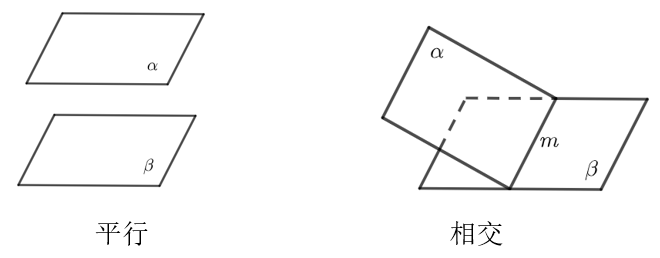
【例】在长方体中\(ABCD-A'B'C'D'\)中,说下平面\(CC'D'D\)与哪些平面相交、平行?

解 平面\(CC'D'D\)与平面\(ADD'A'\)相交于直线\(DD'\),与平面\(AB'C'D\)相交于直线\(DC'\);与平面\(ABB'A'\)平行. (答案不唯一)
基本方法
【题型1】 空间两条直线位置关系的判定
【典题1】 在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(E\),\(F\)分别是\(AA_1\),\(AB\)的中点,试判断下列 各对线段所在直线的位置关系:

(1)\(AB\)与\(CC_1\);\(\qquad \qquad\) (2)\(A_1 B_1\)与\(D C\);\(\qquad \qquad\) (3)\(A_1 C\)与\(D_1 B\);\(\qquad \qquad\) (4)\(DC\)与\(BD_1\);\(\qquad \qquad\) (5)\(D_1 E\)与\(CF\).
解析 (1)\(\because C\in\)平面\(ABCD\),\(AB\subset\) 平面\(ABCD\),又\(C\notin AB\),\(C_1\notin\) 平面\(ABCD\),
\(\therefore AB\)与\(CC_1\)异面.
(2)\(\because A_1 B_1∥AB\),\(AB∥DC\),\(\therefore A_1 B_1∥DC\).
(3)\(\because A_1 D_1∥BC\),则\(A_1\),\(B\),\(C\),\(D_1\)在同一平面内,\(\therefore A_1 C\)与\(D_1 B\)相交.
(4)\(\because B\in\)平面\(ABCD\),\(DC\subset\) 平面\(ABCD\),又\(B\notin DC\),\(D_1\notin\) 平面\(ABCD\),
\(\therefore DC\)与\(BD_1\)异面.

(5)连接\(A_1 B\),\(EF\),\(D_1 C\),则\(A_1 B∥D_1 C\).
又\(E\),\(F\)分别是\(AA_1\),\(AB\)的中点,\(\therefore EF∥\dfrac{1}{2} A_1 B\).
\(\therefore EF∥\dfrac{1}{2} D_1 C\),\(\therefore\) 四边形\(CD_1 EF\)是梯形,\(D_1 E\)与\(CF\)是腰.
\(\therefore D_1 E\)与\(CF\)相交.
【典题2】如图,点\(A\notin α\),\(B\in α\),\(B\notin l\),\(l\subset α\),求证: 直线\(AB\)与直线\(l\)是异面直线.

解析 假设直线\(AB\)与直线不是异面直线,设它们所在的平面为\(\beta\) .
由\(B\in \beta\) ,\(l\subset \beta\),而\(B\in \alpha\),\(l\subset \alpha\),且\(B\notin l\),则\(\alpha\) 与\(\beta\)重合.
又\(AB\subset \beta\),则\(AB\subset \alpha\),得\(A\in \alpha\),与\(A\notin \alpha\)矛盾.
所以假设不成立,即直线\(AB\)与直线\(l\)是异面直线.
点拨 利用反证法证明.
【巩固练习】
1.异面直线是指( )
A.空间中两条不相交的直线
B.分别位于两个不同平面内的两条直线
C.平面内的一条直线与平面外的一条直线
D.不同在任何一个平面内的两条直线
2.已知\(a\)、\(b\)是异面直线,\(P\)是\(a\)、\(b\)外一点,经过点\(P\)且与\(a\)、\(b\)都相交的直线有( )
A.至少\(1\)条 \(\qquad\) B.最多\(1\)条 \(\qquad\) C.有且只有\(1\)条 \(\qquad\) D.可能为\(0\)条也有可能多于\(1\)条
3.一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是( )
A.平行 \(\qquad \qquad\) B.相交 \(\qquad \qquad\) C.异面 \(\qquad \qquad\)D. 相交或异面
4.若\(a\),\(b\)是异面直线,下列四个命题中正确的是( )
A.过不在\(a\)、\(b\)上任一点\(P\),必可作直线与\(a\)、\(b\)都平行
B.过不在\(a\)、\(b\)上任一点\(P\),必可作直线与\(a\)、\(b\)都相交
C.过不在\(a\)、\(b\)上任一点\(P\),必可作直线与\(a\)、\(b\)都垂直
D.过不在\(a\)、\(b\)上任一点\(P\),必可作平面与\(a\)、\(b\)都平行
5.如图所示,\(G\)、\(H\)、\(M\)、\(N\)分别是正三棱柱的顶点或所在棱的中点,则表示直线\(GH\),\(MN\)是异面直线的图形有 \(\underline{\quad \quad}\) (填序号).

6.如图,是一个正方体的展开图,如果将它还原为正方体,那么\(AB\),\(CD\),\(EF\),\(GH\)这四条线段所在直线是异面直线的有\(\underline{\quad \quad}\)对.

7.如图所示,正方体\(ABCD—A_1 B_1 C_1 D_1\)中,\(M\)、\(N\)分别是\(A_1 B_1\)、\(B_1 C_1\)的中点.问
(1)\(AM\)和\(CN\)是否是异面直线?说明理由;
(2)\(D_1 B\)和\(CC_1\)是否是异面直线?说明理由.

参考答案
-
答案 \(D\)
-
答案 \(B\)
解析设\(P\)与\(a\)所确定的平面为\(\alpha\) ,若\(\alpha\) 与\(b\)交于点\(Q\),
当\(PQ\)不平行于\(a\)时,\(PQ\)与异面直线\(a\)、\(b\)都相交,
当\(PQ//a\)或\(b//\alpha\) 时,过点\(P\)与异面直线\(a\)、\(b\)都相交的直线不存在;
则直线\(a\),\(b\)上分别有两点在面\(\beta\)上,所以直线\(a\)、\(b\)在面\(\beta\)内,与\(a\)、\(b\)异面矛盾.
故选: \(B\) -
答案 \(D\)
解析 如图 (1) 所示,此时直线\(a\)与直线\(b\)为异面直线,
其中\(l ||a\),此时直线\(l\)与\(b\)为相交直线;
如图 (2) 所示,此时直线\(a\)与直线\(b\)为异面直线,其中\(l||a\),此时直线\(l\)与\(b\)为异面直线,
综上,一条直线与两条异面直线中的一条平行,则它和另一条直线的位置关系是相交或异面.
故选: \(D\).

-
答案 \(C\)
解析如图所示,\(a\)、\(b\)是异面直线,
设不在\(a\)、\(b\)上的任意一点为\(P\).假设过点\(P\)可作直线\(l∥a\),\(l∥b\),则\(a∥b\),这与已知\(a\)、\(b\)是异面直线相矛盾.因此假设不成立,即不存在过点\(P\)的直线\(l\)与\(a\)、\(b\)都平行.
所以\(A\)不正确.
若点\(P\in \alpha\)或\(P\in \beta\),则不能够作直线\(l\)与\(a\)、\(b\)都相交,因此\(B\)不正确;
过点\(P\)一定可作直线\(l⊥\alpha\) ,\(\because \alpha ∥\beta\),\(a\subset \alpha\),\(b\subset \beta\),则\(l⊥a\),\(l⊥b\).
因此\(C\)正确.
若点\(P\in \alpha\) 或\(P\in \beta\) ,则不能够作平面与\(a\)、\(b\)都平行,因此\(D\)不正确;
故选:\(C\).

-
答案 ②④
解析 由题意可得图①中\(GH\)与\(MN\)平行,不合题意;
图②中的\(GH\)与\(MN\)异面,符合题意;
图③中\(GH\)与\(MN\)相交,不合题意;
图④中\(GH\)与\(MN\)异面,符合题意.
故答案 为:②④ -
答案 \(3\)
解析 如图所示 把展开图再还原成正方体,由经过平面外一点和平面内一点的直线和平面内不经过该点的直线是异面直线可得,\(AB\),\(CD\),\(EF\),\(GH\)这四条线段所在直线是异面直线的有\(AB\) 和\(CD\),\(AB\)和\(HG\),\(EF\)和 \(HC\),共三对,

-
答案 (1)不是;(2)是
解析 (1)不是异面直线.理由如下
连接\(MN\)、\(A_1 C_1\) 、\(AC\).
\(\because M\)、\(N\)分别是\(A_1 B_1\) 、\(B_1 C_1\)的中点,\(\therefore MN∥A_1 C_1\).
又\(\because A_1 A=C_1 C\),\(A_1 A∥C_1 C\),\(\therefore A_1 ACC_1\)为平行四边形,
\(\therefore A_1 C_1∥AC\),\(\therefore MN∥AC\),
\(\therefore A\)、\(M\)、\(N\)、\(C\)在同一平面内,故\(AM\)和\(CN\)不是异面直线.
(2)是异面直线.证明如下
\(\because ABCD—A_1 B_1 C_1 D_1\)是正方体,\(\therefore B\)、\(C\)、\(C_1\) 、\(D_1\)不共面.
假设\(D_1 B\)与\(CC_1\)不是异面直线,
则存在平面\(\alpha\),使\(D_1 B\subset\)平面\(\alpha\) ,\(CC_1\subset\)平面\(\alpha\) ,
\(\therefore D_1\)、\(B\)、\(C\)、\(C_1\in \alpha\),与\(ABCD—A_1 B_1 C_1 D_1\)是正方体矛盾.
\(\therefore\)假设不成立,即\(D_1 B\)与\(CC_1\)是异面直线.

【题型2】线面、面面的位置关系
【典题1】 直线\(a\)与平面\(\alpha\)不平行,则\(\alpha\) 内与\(a\)平行的直线有( )
A. 无数条 \(\qquad \qquad \qquad\) B. \(0\)条 \(\qquad \qquad \qquad\) C. \(1\) 条 \(\qquad \qquad \qquad\) D.以上均不正确
解析 因为直线\(a\)与平面\(\alpha\)不平行,所以直线\(a\)与平面\(\alpha\) 的关系有两种,
即\(a\subset \alpha\)以及直线\(a\)与平面\(\alpha\) 相交.
当\(a\subset \alpha\)时,显然在\(\alpha\)内与\(a\)平行的直线有无数条;
当直线\(a\)与平面\(\alpha\)相交时,设\(a∩\alpha =A\).
当\(b\subset \alpha\),且\(A\in b\)时,此时\(a∩b=A\),即直线\(a\)、\(b\)相交;
当\(b\subset a\),且\(A\notin b\)时,可知直线\(a\)、\(b\)异面.
综上所述,当直线\(a\)与平面\(\alpha\) 相交时,\(\alpha\)内与\(a\)平行的直线有\(0\)条.
所以,直线\(a\)与平面\(\alpha\) 不平行,则\(\alpha\)内与\(a\)平行的直线有无数条或\(0\)条.
故选:\(D\).
【典题2】 平面\(\alpha\)上有三个不共线点到平面\(\beta\)距离相等,则平面\(\alpha\)与平面\(\beta\)的位置关系是( )
A. 相交 \(\qquad \qquad \qquad\) B.平行 \(\qquad \qquad \qquad\)C.垂直 \(\qquad \qquad \qquad\) D.相交或平行
解析 如图\(1\),若\(\alpha ∥\beta\) ,则平面\(\alpha\)上任一点到平面\(\beta\) 距离相等,
故平面\(\alpha\)上一定存在三个不共线点到平面\(\beta\)距离相等;
如图2,若\(\alpha\) 与\(\beta\)相交,则平面\(\alpha\)上一定存在位于异侧的三个不共线点到平面\(\beta\)距离相等;
故平面\(\alpha\)与平面\(\beta\)的位置关系是相交或平行. 故选: \(D\).

【巩固练习】
1.下列命题中正确的个数是 ( )
①若直线\(l\)上有无数个点不在平面\(a\)内,则\(l∥a\).
②若直线\(l\)与平面\(a\)平行,则\(l\)与平面\(a\)内的任意一条直线都平行.
③如果两条平行直线中的一条与一个平面平行∙,那么另一条也与这个平面平行.
④若直线\(l\)与平面\(a\)平行,则\(l\)与平面\(a\)内的任意一条直线都没有公共点.
A.\(0\) \(\qquad \qquad\qquad \qquad\) B.\(1\) \(\qquad \qquad\qquad \qquad\) C.\(2\) \(\qquad \qquad\qquad \qquad\) D.\(3\)
2.若直线\(a\)在平面\(\gamma\)外,则( )
A.\(a∥\gamma\) \(\qquad \qquad\) B.\(a\)与\(\gamma\)至少有一个公共点 \(\qquad \qquad\) C.\(a∩\gamma=A\) \(\qquad \qquad\) D.\(a\)与\(\gamma\)至多有一个公共点
3.平面\(\alpha\)与平面\(\beta\),\(\gamma\)都相交,则这三个平面可能有( )
A.\(1\)条或\(2\)条交线 \(\qquad \qquad \qquad\) B.\(2\)条或\(3\)条交线
C.仅\(2\)条交线 \(\qquad \qquad \qquad\) D.\(1\)条或\(2\)条或\(3\)条交线
4.若直线\(a\)在平面\(M\)内,直线\(m\)平行直线\(a\),则直线\(m\)与平面\(M\)的位置关系是\(\underline{\quad \quad}\) .
5.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成\(\underline{\quad \quad}\)部分.
参考答案
-
答案 \(B\)
-
答案 \(D\)
解析 \(\because\)直线\(a\)在平面\(\gamma\)外,
\(\therefore\)直线\(a∥\)平面\(\gamma\)或直线\(a\)与平面\(\gamma\)相交,
直线\(a∥\)平面\(\gamma\)时,\(a\)与\(\gamma\)没有公共点,
当直线\(a\)与平面\(\gamma\)相交时,\(a\)与\(\gamma\)有一个公共点.
\(\therefore a\)与\(\gamma\)至多有一个公共点.
故选:\(D\). -
答案 \(D\)
解析 ①若平面\(\beta ∥\)平面\(\gamma\),平面\(\alpha\)与平面\(\beta\),\(\gamma\)都相交,则它们有\(2\)条交线,且这\(2\)条交线互相平行;
②若平面\(\beta \cap\)平面\(\gamma=a\),平面\(\alpha\)是经过直线\(a\)的平面,则三个平面只有一条交线,即直线\(a\);
③若平面\(\beta \cap\)平面\(\gamma=a\),平面\(\alpha\) 与平面\(\beta\),\(\gamma\)都相交,但交线与直线\(a\)不重合,则它们有\(3\)条交线,
例如棱柱或棱锥的三个侧面相交于三条直线,即三条侧棱
综上所述,这三个平面的交线的条数可能是\(1\)条、\(2\)条或\(3\)条
故选\(D\) -
答案 \(m||M\)或者\(m\subset M\).
-
答案 \(7\)
解析 如图所示,三个平面\(\alpha\) 、\(\beta\)、\(\gamma\)两两相交,交线分别是\(a\)、\(b\)、\(c\)且\(a∥b∥c\).
观察图形,得\(\alpha\) 、\(\beta\)、\(\gamma\)把空间分成\(7\)部分.
故答案 为:\(7\).

分层练习
【A组---基础题】
1.两条异面直线指的是 ( )
A.不同在任何一个平面内的两条直线
B.在空间内不相交的两条直线
C.分别位于两个不同平面内的直线
D.某一个平面内的一条直线和这个平面外的一条直线
2.若\(l_1\),\(l_2\)为异面直线,直线\(l_3∥l_1\),则\(l_3\) 与\(l_2\)的位置关系是( )
A.相交 \(\qquad \qquad \qquad\) B.异面 \(\qquad \qquad \qquad\)C.平行 \(\qquad \qquad \qquad\) D.异面或相交
3.若直线\(l\)不平行于平面\(\alpha\),且\(l⊄\alpha\),则( )
A.\(\alpha\) 内所有直线与\(l\)异面 \(\qquad \qquad \qquad\) B.\(\alpha\)内不存在与\(l\)平行的直线
C.\(\alpha\)内存在唯一的直线与\(l\)平行 \(\qquad \qquad\) D.\(\alpha\)内的直线与\(l\)都相交
4.分别和两条异面直线都相交的两条直线一定是 ( )
A.异面直线 \(\qquad \qquad\) B.相交直线 \(\qquad \qquad\) C.不相交直线 \(\qquad \qquad\)D.不平行直线
5.如果三个平面将空间分成\(6\)个互不重叠的部分,则这三个平面的位置是 ( )
A.两两相交于三条交线
B.两个平面互相平行,另一平面与它们相交
C.两两相交于同一条直线
D.\(B\)中情况或\(C\)中情况都可能发生
6.(多选)如图,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\),\(N\)分别为棱 \(C_1 D_1\),\(C_1 C\)的中点,则以下四个结论中,正确的有( )

A. 直线\(AM\)与\(CC_1\)是相交直线 \(\qquad \qquad\) B.直线\(BN\)与\(MB_1\)是异面直线
C.\(AM\)与\(BN\)平行 \(\qquad \qquad \qquad \qquad\) D.直线\(A_1 M\)与\(BN\)共面
7.已知三条直线\(a\),\(b\),\(c\),\(a\)与\(b\)异面,\(b\)与\(c\)异面,则\(a\)与\(c\)的位置关系是\(\underline{\quad \quad}\).
8.平面外的直线上有两个点到平面\(\alpha\)距离相等,则直线与平面的位置关系是\(\underline{\quad \quad}\) .
9.若三个平面两两相交,则它们的交线条数是\(\underline{\quad \quad}\)条
参考答案
-
答案 \(A\)
解析 两条异面直线指的是不同在任何一个平面内的两条直线,故\(A\)正确;
空间中不相交的两条直线可以平行或异面,故\(B\)错误;
分别位于两个不同平面内的两条直线可以平行、相交或异面,故\(C\)错误;
某一个平面内的一条直线和这个平面外的一条直线可以平行、相交或异面,故\(D\)错误.
故选: \(A\) -
答案 \(D\)
解析 \(\because l_1\),\(l_2\)为异面直线,
\(\therefore\)直线\(l_1\),\(l_2\)所成角为锐角或直角
\(\because l_3∥l_1\),
\(\therefore\) 直线\(l_3\)与\(l_2\)的所成角为锐角或直角
由此可得:\(l_3\)与\(l_2\)不平行,即直线\(l_3\)与\(l_2\)的位置关系为相交或异面
故选:\(D\). -
答案 \(B\)
解析 \(\alpha\)内与\(l\)相交的直线在同一面内,故\(A\)选项错误.
直线\(l\)与面相交的点,过此点的所有直线均与\(l\)相交,平面内其他的线则不与其相交,故C,\(D\)项说法错误.
若\(\alpha\)内存在与\(l\)平行的直线,则根据线面平行的判定定理可知\(l\)与面\(\alpha\)平行,已知直线\(l\)不平行于平面\(\alpha\) ,
故\(\alpha\)内不存在与\(l\)平行的直线,\(B\)项说法正确.
故选:\(B\). -
答案 \(A\)
解析 已知直线\(a\)与\(b\)是异面直线,直线AB与直线CD分别与两条直线\(a\)与直线\(b\)相交与点\(A\),\(B\),\(C\),D,

根据题意可得当点\(D\)与点\(B\)重合时,两条直线相交,当点\(D\)与点\(B\)不重合时,两条直线异面.
下面证明两条直线不平行
假设直线\(AB\)与直线CD平行,则\(A\),\(B\),C,\(D\)四点共面,
所以直线\(BD\)与直线\(AC\)共面,
这与直线\(a\)、直线\(b\)异面相互矛盾,
所以假设错误,即直线\(AB\)与直线CD不平行.
所以分别与两条异面直线都相交的两条直线一定不平行.
故选\(A\). -
答案 \(D\)
解析 \(A\)选项中,若三个平面两两相交,且有三条交线,则把空间分成\(7\)或\(8\)部分;故\(A\)不正确.
\(B\)选项中,若两个平面互相平行,另一平面与它们相交,则把空间分成\(6\)部分;故\(B\)正确.
\(C\)选项中,若三个平面两两相交于同一条直线,则把空间分成\(6\)部分;故\(C\)正确.
故选 \(D\). -
答案 \(BD\)
解析 \(A\)选项,\(\because A\)、\(M\)、\(C\)、\(C_1\)四点不共面,
\(\therefore\)根据异面直线的定义可得直线\(AM\)与\(CC_1\)是异面直线,故选项\(A\)错误;
\(B\)选项,\(\because B\)、\(N\)、\(M\)、\(B_1\)四点不共面,
\(\therefore\)根据异面直线的定义可得直线\(BN\)与\(MB_1\)是异面直线,故选项\(B\)正确;
\(C\)选项,取\(DD_1\)的中点\(E\),连接\(AE\)、\(EN\),则有\(AB//EN\),\(AB=EN\),
所以四边形\(ABNE\)是平行四边形,所以\(AE//BN\),

\(\because AM\)与\(AE\)交于点\(A\),\(\therefore AM\)与\(AE\)不平行,则\(AM\)与\(BN\)不平行,故选项\(C\)错误;
\(D\)选项,连接\(A_1 M\)、\(MN\)、\(NB\)、\(BA_1\),\(CD_1\),
因为\(M\),\(N\)分别为棱\(C_1 D_1\),\(C_1 C\)的中点,
所以\(MN//D_1 C\),由正方体的性质可知:\(BA_1//D_1 C\),
所以\(MN//A_1 B\),\(\therefore A_1\) 、\(B\)、\(M\)、\(N\)四点共面,
\(\therefore 直线A_1 M\)与\(BN\)共面,故选项\(D\)正确.
故选: \(BD\). -
答案 相交、平行或异面
-
答案 平行或相交
解析 平面外的直线与平面的关系为: 直线与平面平行或直线与平面相交.
当直线与平面平行时,显然满足直线上有两个点到平面\(\alpha\)距离相等;
当直线与平面相交时,

如图正方体中,点\(E\)、\(F\)、\(G\)、\(H\)分别是各棱的中点.
根据正方体的性质可知,\(BF⊥\)平面\(EFGH\),\(D_1 H⊥\)平面\(EFGH\),且\(BF=D_1 H\),
即直线\(BD_1\)上存在两点\(B\)、\(D_1\)到平面\(EFGH\)的距离相等,且直线\(BD_1\)与平面\(EFGH\)相交.
故答案 为: 平行或相交. -
答案 \(1\)或\(3\)
解析 如图,三个平面有一条交线的情况,

三个平面有两条交线的情况,
