2.3 常用的离散型分布
退化分布
若随机变量\(X\)满足
\[P\{X=a\}=1 \]则称\(X\)服从\(a\)处的退化分布,这种情况下,随机变量退化成了一个确定的常数。
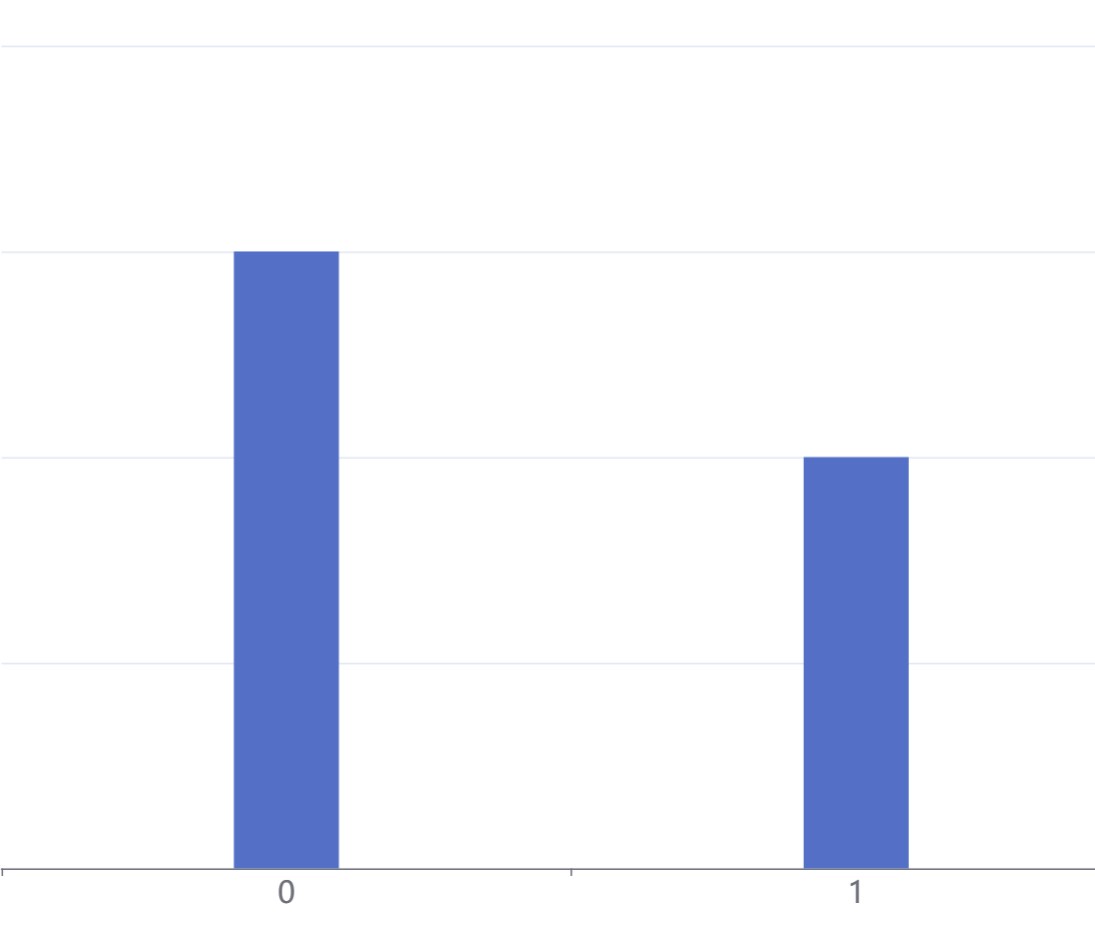
两点分布
定义
若随机变量\(X\)只有两个可能取值,设其分布为
\[P\{X=x_1\}=p,\quad P\{X=x_2\}=1-p,\quad 0<p<1, \]则称\(X\)服从\(x_1,x_2\)处参数为\(p\)的两点分布。
如果\(x_1=1,x_2=0\),则称为0-1分布或伯努利分布,也称\(X\)为伯努利随机变量。
性质
当\(x_1=1,x_2=0\)时,有\(EX=p,\quad DX=p(1-p)=pq\),其中\(q=1-p\).
两点分布也可以表示为:\(P\{X=k\}=p^k(1-p)^{1-k},\quad k=0,1\)
两点分布是二项分布的特例
联系
伯努利试验
图像
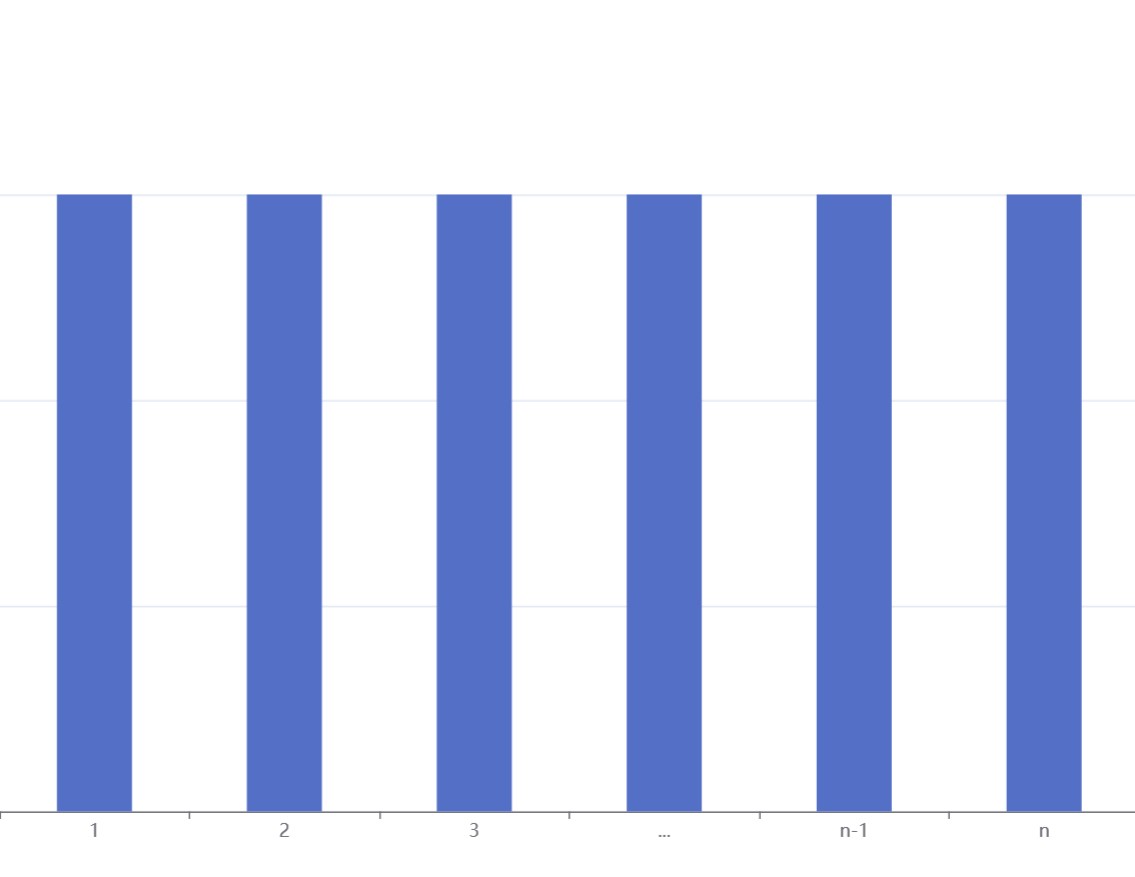
n个点上的均匀分布
定义
如果随机变量\(X\)的分布满足
\[P\{X=x_i\}=\frac{1}{n},\quad i=1,2,\cdots,n, \]则称\(X\)服从\(n\)个点\(\{x_1,x_2,\cdots,x_n\}\)上的均匀分布。
性质
\(EX=\frac{1}{n}\sum\limits_{i=1}^nx_i=\overline{x}\)
\(DX=\frac{1}{n}\sum\limits_{n-1}^n(x_i-\overline{x})^2\)
数学期望的本质是加权平均数,权重就是对应的概率,在均匀分布中,每个权重都是相等的,所以数学期望就等于算术平均数。
联系
古典概型
图像
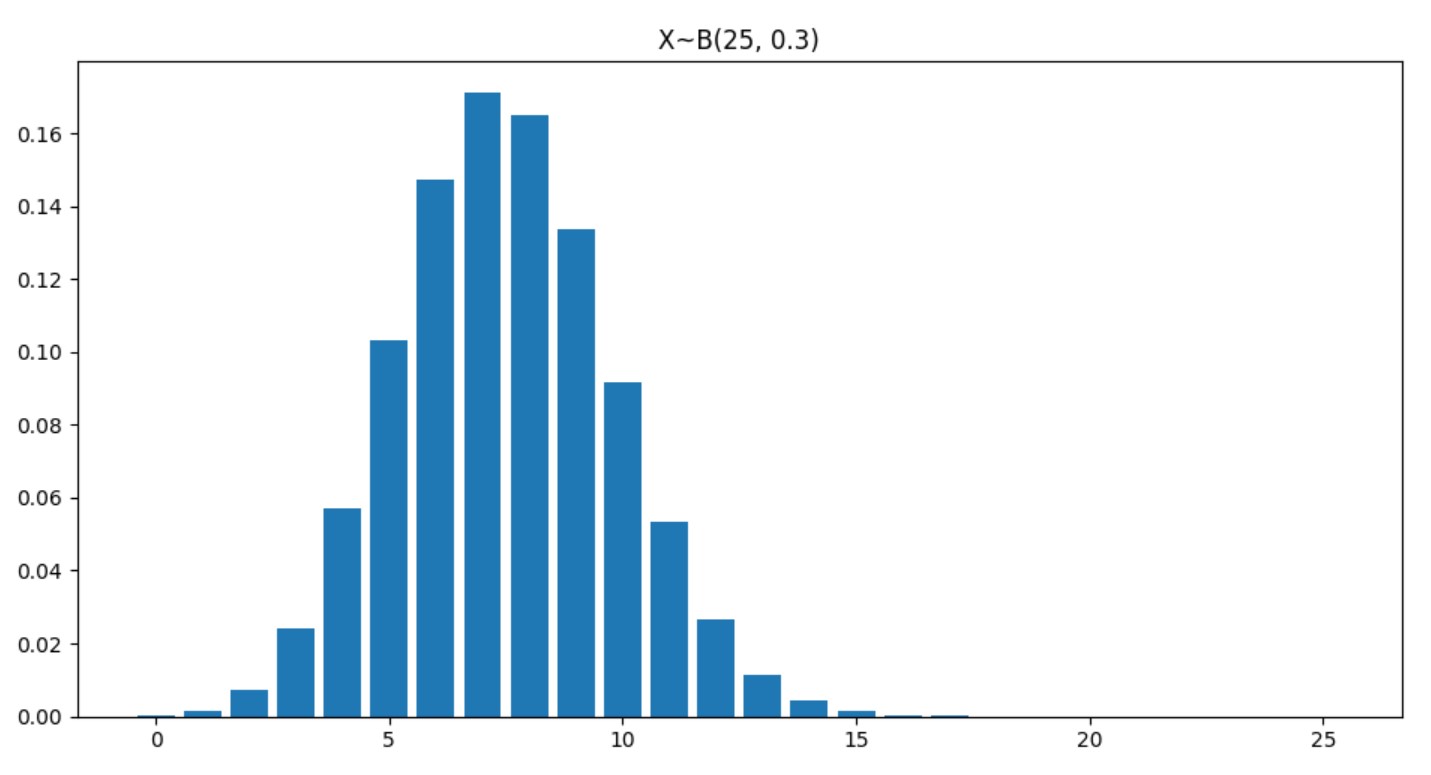
二项分布
定义
事件\(A\)发生的概率为\(p\),\(n\)次试验,发生了\(k\)次。
如果\(X\)的分布满足
\[P\{X=k\}=C_n^kp^k(1-p)^{n-k},\quad k=0,1,2,\cdots,n, \]则称\(X\)服从参数为\(n,p\)的二项分布,并记作\(X\sim B(n,p)\).
记\(B(k;n,p)=C_n^kp^k(1-p)^{n-k}\).
当\(n=1\)时,二项分布\(B(1,p)\)就是参数为\(p\)的0-1分布。
性质
- 最可能值
- 若\((n+1)p\)不为整数,则\([(n+1)p]\)达最大值,其中\(f(x)=[x]\)是取整函数。
- 若\((n+1)p\)为正数,则$(n+1)p,\ \ (n+1)p-1 $是最大值。
- 数学期望:\(EX=np\)
- 方差:\(DX=npq\)
联系
\(n\)重伯努利试验
图像
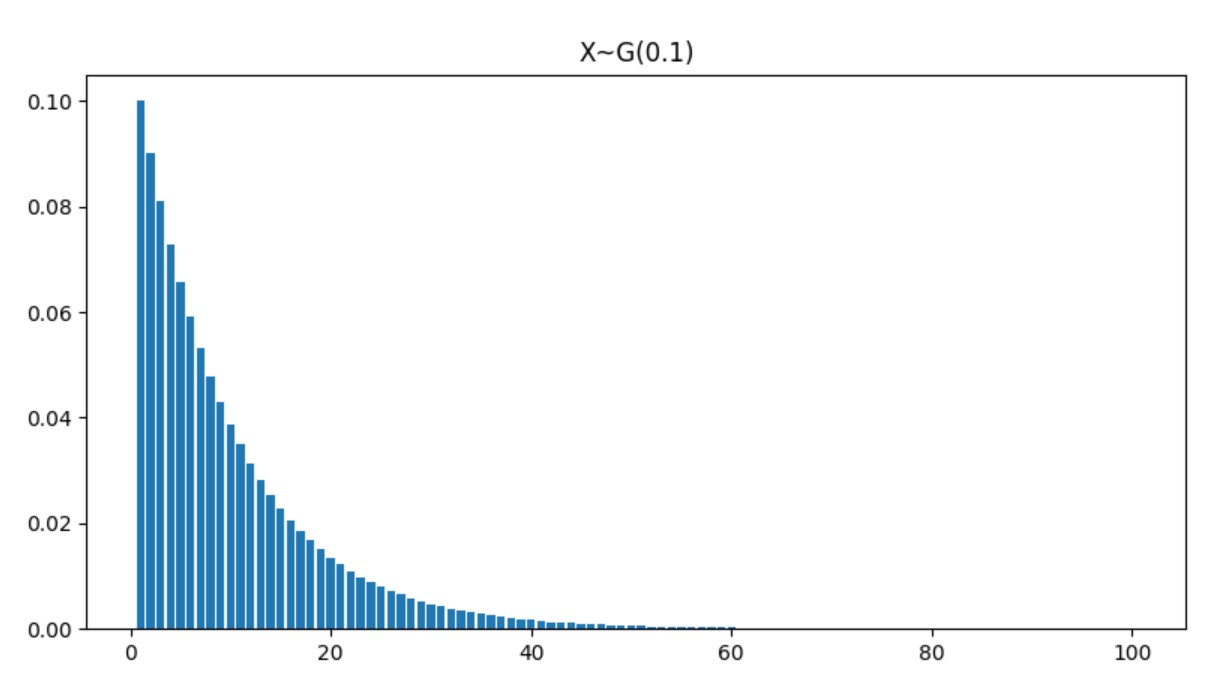
几何分布
定义
\(P(A)=p\),第\(k\)次首次发生,前\(k-1\)次不发生的概率为
\[P\{X=k\}=(1-p)^{k-1}p=q^{k-1}p,\quad k\ge1 \]这样的分布就叫几何分布,记为\(X\sim G(p)\).
之所以称为“几何”是因为\(q^{k-1}p\)是一个几何数列(也叫等比数列)。
性质
- 数学期望:\(EX=\frac{1}{p}\)
- 方差:\(DX=\frac{q}{p^2}\)
- 无记忆性:\(P\{X>m+n|X>m\}=P\{X>n\}\)
对于无记忆性的理解:就算之前做过了\(m\)次试验,对于接下来的\(n\)次试验是没有影响的。
计算
- \(P\{X=k\}=q^{k-1}p\)
- \(P\{X>m\}=\sum\limits_{k=m+1}^\infty q^{k-1}p\)
图像
超几何分布
定义
\(N\)个元素分为两类,个数分别为\(N_1,N_2\),即\(N=N_1+N_2\)。从\(N\)个元素中取出\(n\)个元素,设随机变量\(X\)为\(n\)个元素中属于第一类元素的个数,则
\[P\{X=k\}=\frac{C_{N_1}^kC_{N_2}^{n-k}}{C_N^n},\quad k=0,1,2,\cdots.min\{n,N_1\} \]
该分布称为超几何分布,记作\(X\sim H(N,n,N_1)\),(也有\(X\sim H(N,N_1,n)\)的记法)。
有时候会把\(N_1,N_2\)记作\(M,N-M\).
\(X\sim H(N,n,M)\)或\(X\sim H(N,M,n)\)
联系
- 超几何分布是不放回的抽取,二项分布是放回的抽取。
- 当\(N,N_1,N_2\)很大时,可以用二项分布作为超几何分布的近似:
当\(N\to\infty,N_1\to\infty,N_2\to\infty\),且\(\frac{N_1}{N}\to p,\ \frac{N_2}{N}\to q\),对于任意给定的\(n\)和\(k\),有
\[\lim\limits_{N\to\infty}\frac{C_{N_1}^kC_{N_2}^{n-k}}{C_N^n}=C_n^kp^kq^{n-k} \]理解:当\(N_1\)和\(N_2\)都很大时,从中拿走一个不放回,数量几乎不变,相当于放回。
性质
- 数学期望:\(EX=n\cdot\frac{N_1}{N}\)
- 方差:\(DX=n\cdot\frac{N_1}{N}\cdot\frac{N_2}{N}\cdot\frac{N-n}{N_1}\)
图像
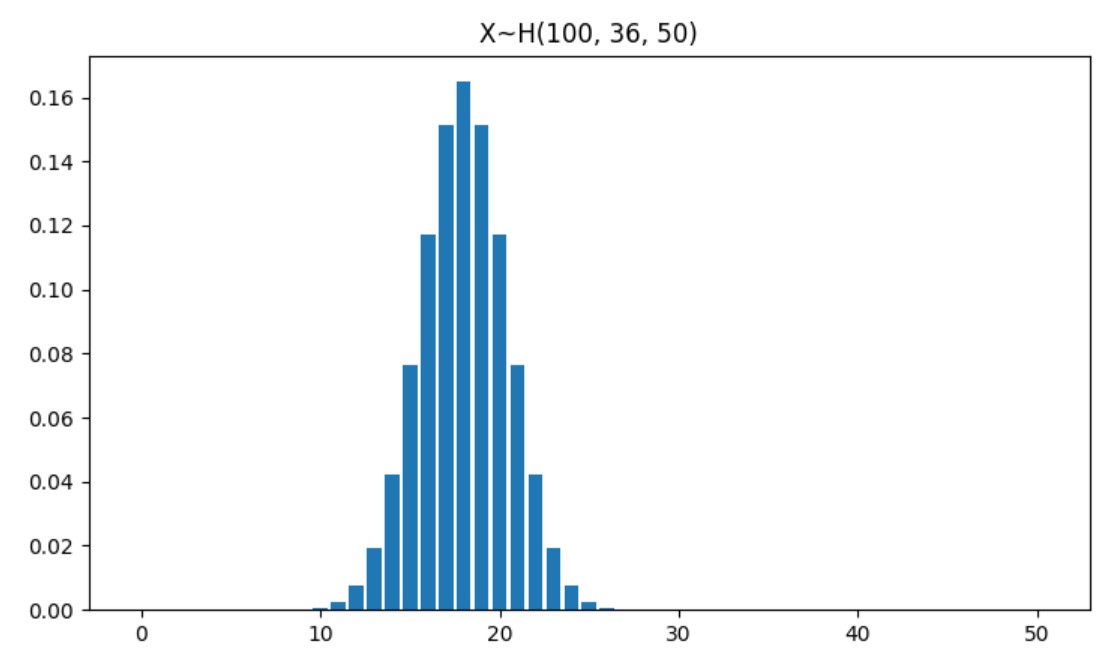
这里的参数分别是\(N=100,\ M=36,\ n=50.\)
泊松分布
定义
如果一个随机变量\(X\)的概率分布为
\[P\{x=K\}=\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0,1,2,\cdots \]其中\(\lambda>0\)为参数,则称\(X\)服从参数为\(\lambda\)的泊松分布,记作\(X\sim P(\lambda)\).
这里的记号\(P\)是指Poisson。
联系
泊松分布可以用于近似表示二项分布,这是因为当二项分布的\(n\to\infty,\ p\to0,\ np=\lambda\)时,二项分布就成为了泊松分布。
泊松定理:在\(n\)重伯努利试验中,事件\(A\)在每次试验中发生的概率为\(p_n\)(这里的概率与试验总数\(n\)有关),如果\(n\to\infty\)时,\(np\to\lambda\)(\(\lambda>0\)为常数),则对任意给定的\(k\),有
\[\lim\limits_{n\to\infty}B(k;n,p)=\lim\limits_{n\to\infty}C_n^kp^k(1-p)^{n-k}=\frac{\lambda^k}{k!}e^{-\lambda} \]证明过程如下:
前提条件有:\(n\to\infty,\ p\to0,\ np=\lambda\),所以有\(p=\frac{\lambda}{n}\).
需要用到的公式:\(C_n^k=\frac{n!}{k!(n-k)!}\),\(\lim\limits_{x\to\infty}(1+\frac{1}{x})^x=e\).
首先,将\(p=\frac{\lambda}{n}\)和组合数公式代入,则
\[\lim\limits_{n\to\infty}C_n^kp^k(1-p)^{n-k}=\lim\limits_{n\to\infty}\frac{n!}{k!(n-k)!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k} \]将\(n!\)和\((n-k)!\)进行化简:
\[\frac{n!}{k!(n-k)!}=\frac{n(n-1)\cdots(n-k+1)}{k!} \]因此,
\[原式=\lim\limits_{n\to\infty}\frac{n(n-1)\cdots(n-k+1)}{k!}\frac{\lambda^k}{n^k}(1-\frac{\lambda}{n})^{n-k} \]此时关注分子的\(n(n-1)\cdots(n-k+1)\),以及分母的\(n^k\)(两者都是有\(k\)项相乘):
\[\begin{align*} \lim\limits_{n\to\infty}\frac{n(n-1)\cdots(n-k+1)}{n^k} &=\lim\limits_{n\to\infty}\frac{n}{n}\cdot\frac{n-1}{n}\cdots\frac{n-k+1}{n} \\ &=\lim\limits_{n\to\infty}1\times(1-\frac{1}{n})\times\cdots\times(1-\frac{k-1}{n}) \\ &=\lim\limits_{n\to\infty}1\times1\times\cdots\times1 \\ &=1 \end{align*} \]因此,
\[原式=\lim\limits_{n\to\infty}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k} \]此时,再关注\(\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k}\),
\[\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k} = \lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n(1-\frac{\lambda}{n})^{-k} \]其中,因为\(n\to\infty\),且\(\lambda,\ k\)都是有限值,所以\((1-\frac{\lambda}{n})\to1\),所以\(\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{-k}=1\)
所以\(\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k}=\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n\)
又因为
\[\begin{align*} \lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n &= \lim\limits_{n\to\infty}(1+\frac{1}{-\frac{n}{\lambda}})^n\quad\quad //\ \lambda从分子移到分母 \\ &= \lim\limits_{n\to\infty}[(1+\frac{1}{-\frac{n}{\lambda}})^{-\frac{n}{\lambda}}]^{-\lambda}\quad\quad //\ 指数拼凑出与自然对数重要极限一致的形式\\ &= e^{-\lambda} \end{align*} \]因此
\[\begin{align*} 原式 &= \lim\limits_{n\to\infty}\frac{\lambda^k}{k!}(1-\frac{\lambda}{n})^{n-k}\\ &= \frac{\lambda^k}{k!}\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^{n-k}\quad\quad//\ 常数提取 \\ &= \frac{\lambda^k}{k!}\lim\limits_{n\to\infty}(1-\frac{\lambda}{n})^n\quad\quad//\ 根据上面的推导 \\ &= \frac{\lambda^k}{k!}e^{-\lambda} \end{align*} \]证明完毕,
\[\lim\limits_{n\to\infty}C_n^kp^k(1-p)^{n-k}=\frac{\lambda^k}{k!}e^{-\lambda} \]证明思路和下面的案例分析来源于B站视频
标签:infty,frac,limits,lim,数理统计,2.3,quad,概率论,lambda From: https://www.cnblogs.com/feixianxing/p/common-discrete-distribution.html