1.4 条件概率
条件概率
- 样本空间\(\Omega\)
- 事件\(A,B\)
- \(P(B)>0\)
在事件\(B\)已经发生的前提条件下,事件\(A\)发生的概率称为A对B的条件概率:\(P(A|B)\).
通常,\(P(A)\)为无条件概率,对应的样本空间为\(\Omega\)。
而条件概率\(P(A|B)\)对应的样本空间为\(B\),或者记为\(\Omega_B\).
所以:
\[P(A|B)=\frac{n_{AB}}{n_B}=\frac{\frac{n_{AB}}{n}}{\frac{n_B}{n}}=\frac{P(AB)}{P(B)} \]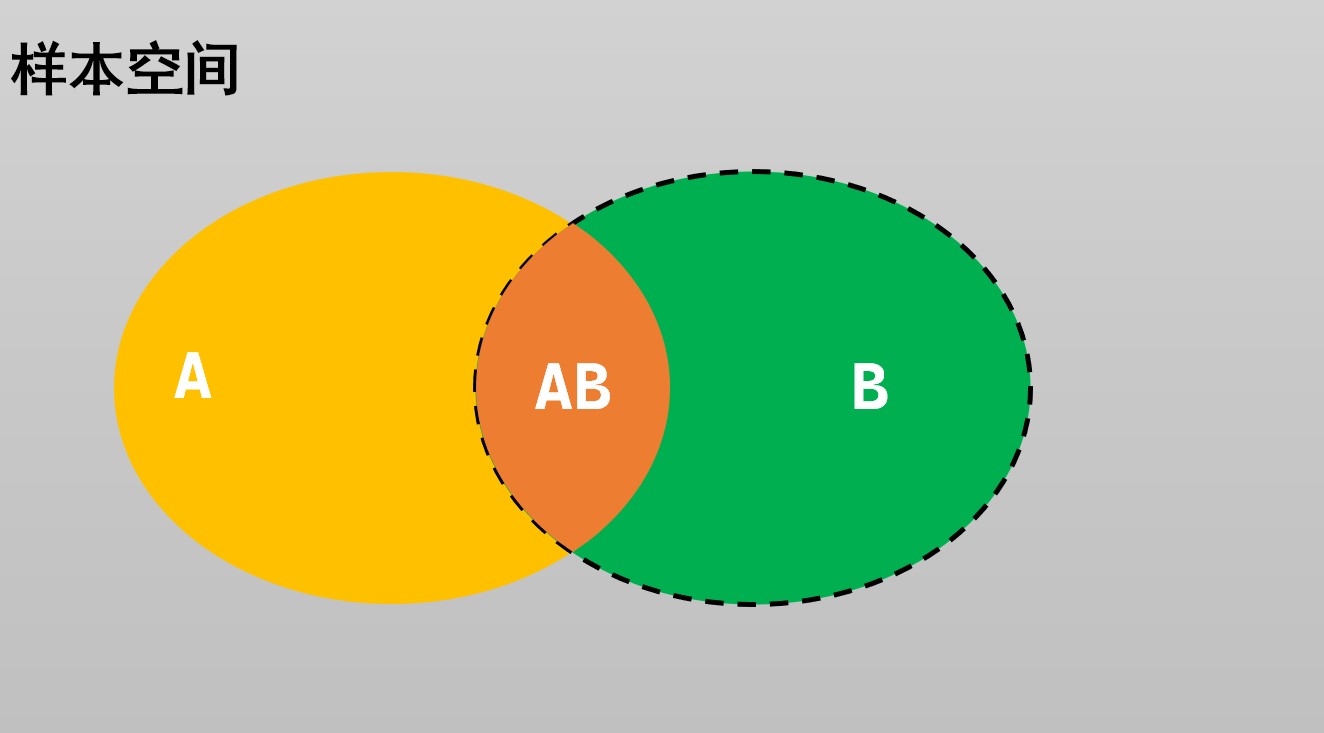
乘法公式
根据\(P(A|B)=\frac{P(AB)}{P(B)}\)可以推导出:
- \(P(AB)=P(A)P(B|A)\)
- \(P(AB)=P(B)P(A|B)\)
其中要求\(P(A)>0,\ P(B)>0\).
乘法公式可以推广到任意有限个事件:
\[P(A_1A_2\cdots A_n)=P(A_1)P(A_2|P_1)P(A_3|A_1A_2)\cdots P(A_n|A_1A_2\cdots A_{n-1}) \]可以理解为逐步画圈,缩小范围直到精准命中指定交集:(这里用\(n=3\)为例)
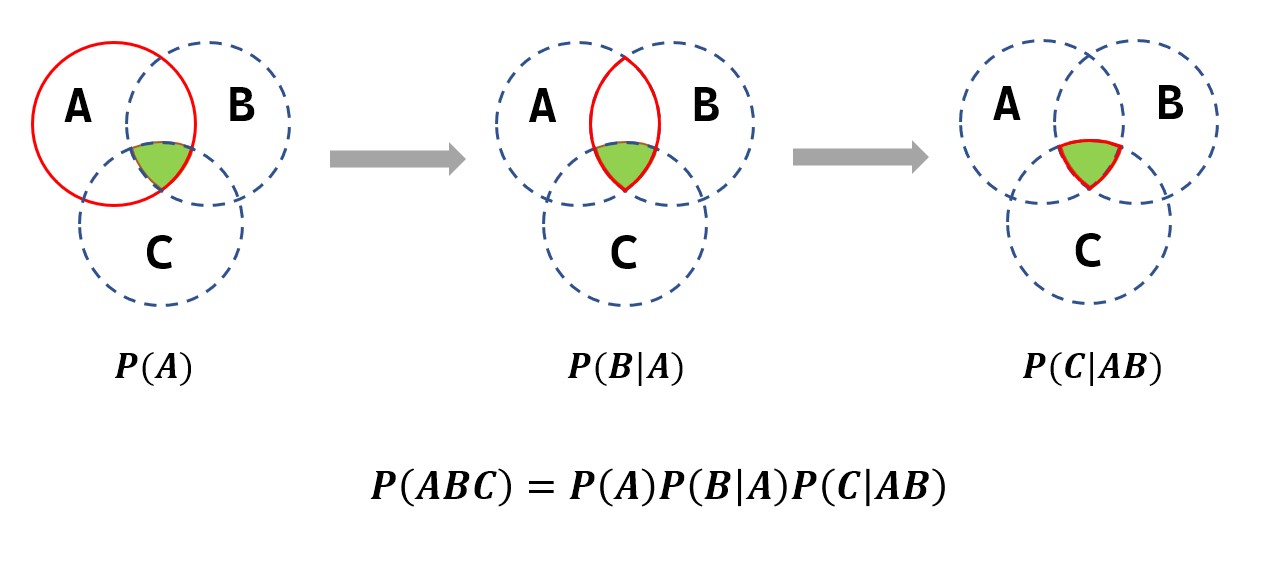
全概率公式
- \(\{A_i\}\)是\(E\)的完备事件组。
- \(P(A_i)>0\)。
则对于任意事件\(B\),有:
\[P(B)=\sum\limits_iP(A_i)P(B|A_i) \]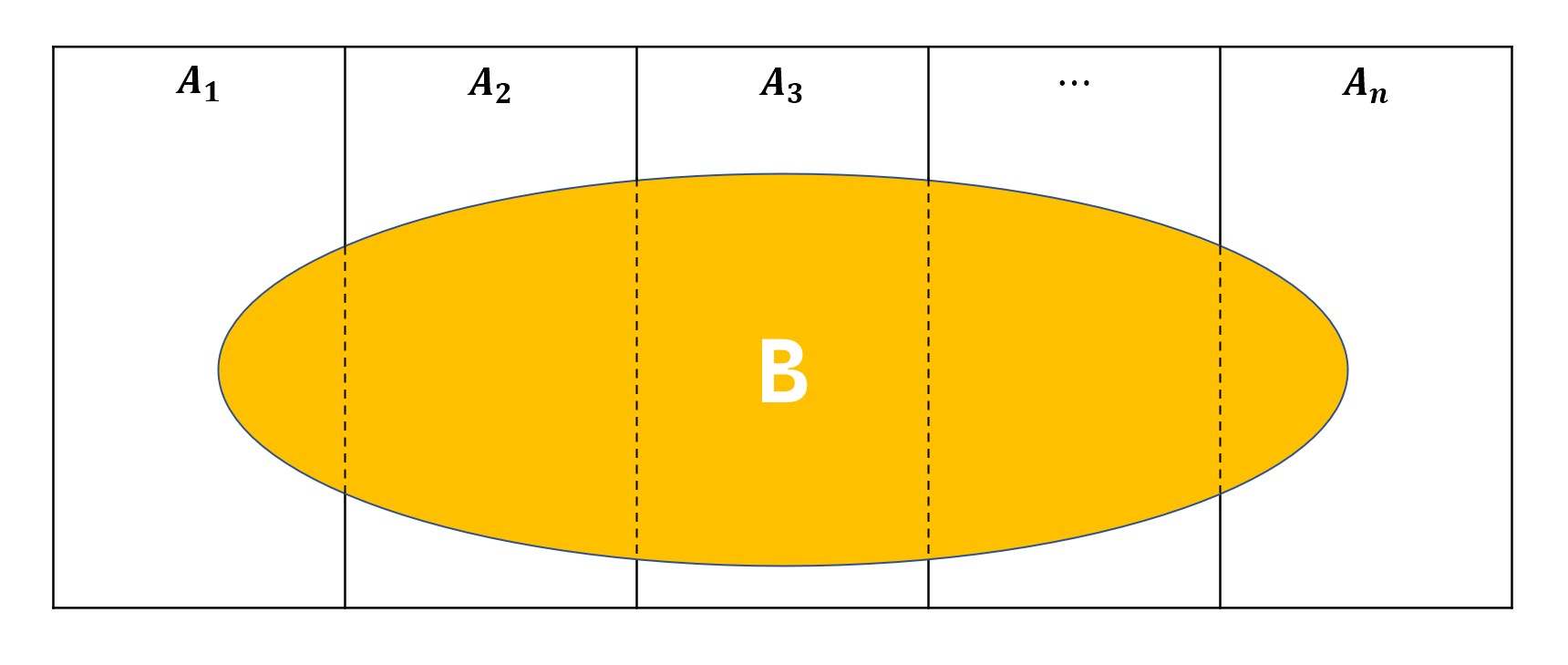
事实上,\(\{A_i\}\)不需要是\(E\)的完备事件集,只需要满足\(\{A_i\}\)的并集能包住\(B\)即可。
贝叶斯公式
定义
- \(\{A_i\}\) 是完备事件组。
- \(P(A_i)>0\).
则对于任意事件\(B\),\(P(B)>0\),有:
\[P(A_i|B)=\frac{P(A_iB)}{P(B)}=\frac{P(A_i)P(B|A_i)}{\sum\limits_iP(A_i)P(B|A_i)} \]- 分子部分:乘法公式
- 分母部分:全概率公式
相关概念
- \(P(A_i)\)称为先验概率(在新信息到来之前)
- \(P(A_i|B)\)称为后验概率(在新信息到来之后)
贝叶斯公式的特点是由果推因,\(A_i\)是原因,\(B\)是结果。在已知\(B\)已经发生的情况下,推测“是\(A_i\)导致的”的可能性。
举例:
事件\(B\)是“头疼”,
事件\(\{A_i\}=\){
"劳累过度",
"普通感冒",
"感染新冠",
......
}
解析:不管事件\(B\)是否发生,事件\(A_i\)都有各自发生的可能性,也就是先验概率\(P(A_i)\)。在事件\(B\)发生之后,后验概率\(P(A_i|B)\)表示“已经头疼了,是由事件\(A_i\)导致的概率是多少”。
注:在这个例子中:
- \(P(A_i|B)\)表示已经头疼了,是由事件\(A_i\)导致的可能性是多少。
- \(P(B|A_i)\)表示事件\(A_i\)已经发生了(比如已经感冒了),那么接下来会“头疼”的可能性是多少。
二者不能搞混。
标签:1.4,概率,frac,公式,cdots,数理统计,AB,事件,概率论 From: https://www.cnblogs.com/feixianxing/p/conditional-probability.html使用教材:
《概率论与数理统计》第四版 中国人民大学 龙永红 主编 高等教育出版社