最近看efficient training方向的论文,发现大学里习得的90多分的线代基本没啥用啊,于是趁着国庆假期重新学习一下。视频内容链接:【熟肉】线性代数的本质 - 00 - “线性代数的本质”系列预览_哔哩哔哩_bilibili
之前只是会算而已,到了需要使用的时候,发现不仅不知道怎么用,连怎么算都忘记了....
向量是啥
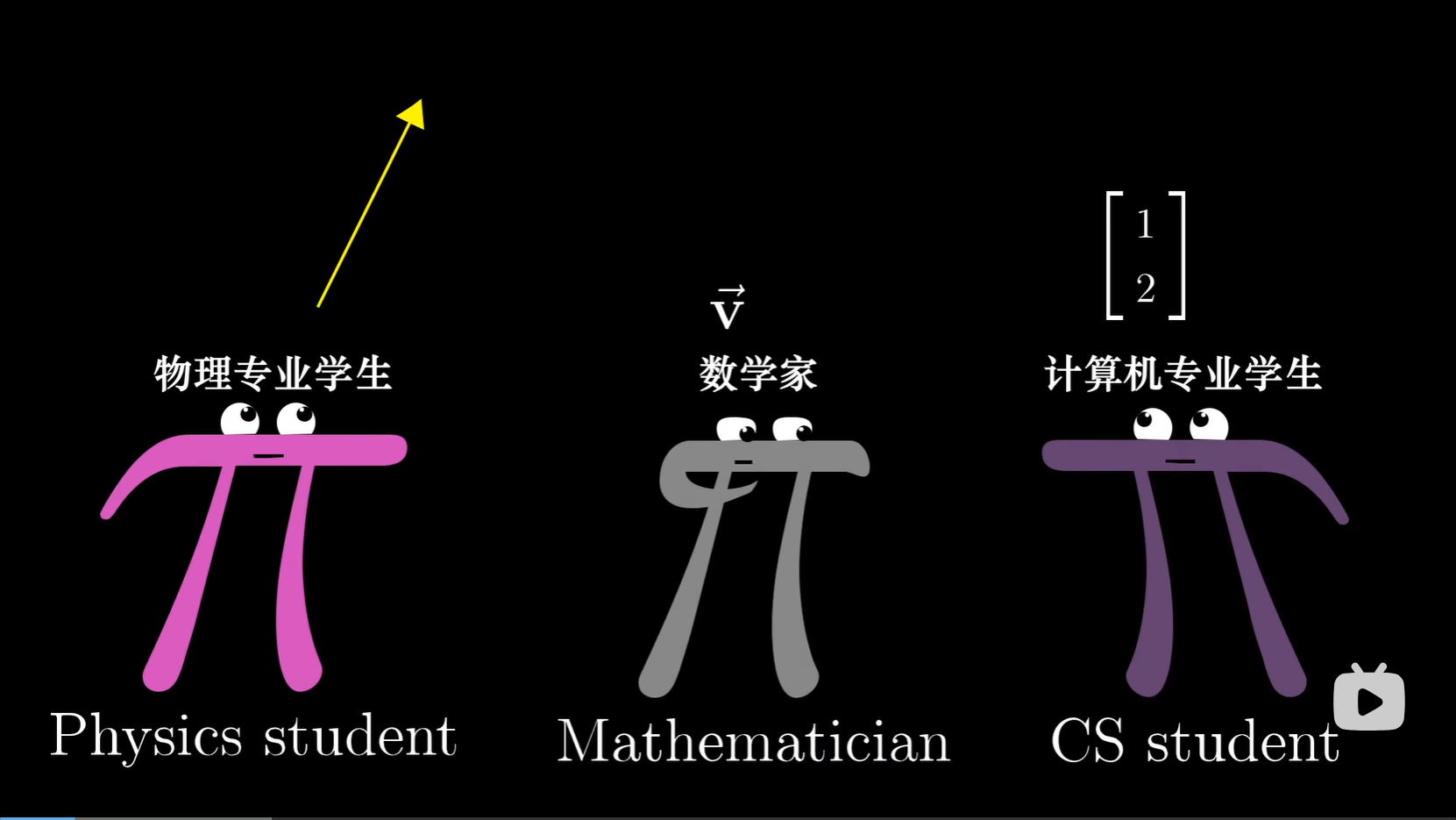
有三种看待向量的视角:
- 物理专业的视角:向量是空间中的箭头,决定一个向量的是它的长度与所指的方向,只要保持这两个特征不变,你可以自由移动这个向量,移动之后它仍然是之前的向量。
- 计算机专业视角:向量是有序的数字列表,注意这里的有序,向量的每一个维度在应用的过程中都是有实际意义的,不能更改它们出现的次序。
- 数学专业的视角:向量是啥都行(列表或者箭头),只要两个向量相加以及数字与向量相乘是有意义的即可。(很符合我对数学的刻板印象,把具体的东西抽象出来,方便运算)
线性组合,张成的空间与基
在二维空间中
当我们用[-2, 3]描述一个向量时(在数学中,如果把向量看成箭头,即如果要在坐标轴中把它表示出来,大部分情况下向量都要从远点出发,而不是像物理中可以随便改变位置),实际上是对两个 基向量 进行缩放在相加的结果,这里的基向量就是x轴y轴上的单位向量:[1, 0], [0, 1]。这两个基向量的全部线性组合:\(a \vec{x} + b \vec{y}\) 构成的向量集合称为“张成的空间”,其中,a,b均为实数。
在一个坐标系中,选择不同的基向量就会有不同的效果,如果两个基向量平行(这个时候它们就不应该称之为基向量),那么它们张成的空间只有一条直线,如果他们都是零向量,那么它们张成的空间就是一个点。
在三维空间中
如果只给你两个基向量,那么你最多也就只能张成一个平面,而不是整个三维空间。
如果给你三个向量,大部分情况下,这三个基向量就能张成整个三维空间,但是,如果其中一个向量能被其他两个向量表示出来,那么这个向量与其他的一个或两个是 线性相关 的,在三维空间中,这三个向量就在一个平面上,这三个中至少有一个是多余的,不管有没有它都不能进一步扩展“张成的空间”。在这种情况下,这三个向量就不能称之三维空间中的基向量。
矩阵与线性变换
线性变化与函数有些类似,它们都是接受一个向量,输出另一个向量。但线性变化更深层次的意思是:将输入向量 移动 到输出向量的位置。
线性变化通常作用于一个空间中的所有向量,一个变化是线性的,它需要满足两个条件:直线仍然是直线,坐标系中的远点固定
一个空间中的向量有无穷多个,我们该如何描述这种变换以及如何确定一个向量变换之后是什么样子的呢?
这里我们只需要知道基向量变换成了什么样子,其他的所有向量都会随着基向量变化

原来的基向量为[1, 0], [0, 1]
对于一个空间的线性变换,只要成功变换了基向量,其实就完成了整个空间的线性变换
对于空间的线性变换,通常默认为变换之前的基向量为[1, 0], [0, 1](这会带来诸多方便,比如变换后的基向量可以直接构成变换矩阵)
从矩阵的角度来看,完成空间中的线性变换实际上就是将原先的向量乘以一个变换矩阵得到变变换后的向量,变换矩阵是有变换后的基向量组成(竖着摆),当然这默认变换前的基向量是标准的基向量
总之,线性变换是操纵空间的一种手段,它保持网格平行并等距分布,并且保持原点不动。这种变化只需要知道变换矩阵或者变换之后的基向量就能描述。
矩阵乘法与线性变换复合

连续进行两种变换可以归结为一种变换
行列式

二维行列式更具体的定义:对于原先有基向量围成的正方形,在空间经过线性变换之后的新的面积
如果行列式为负的话,可以理解为整个空间翻转了
三维就是体积的缩放
二位行列式计算:
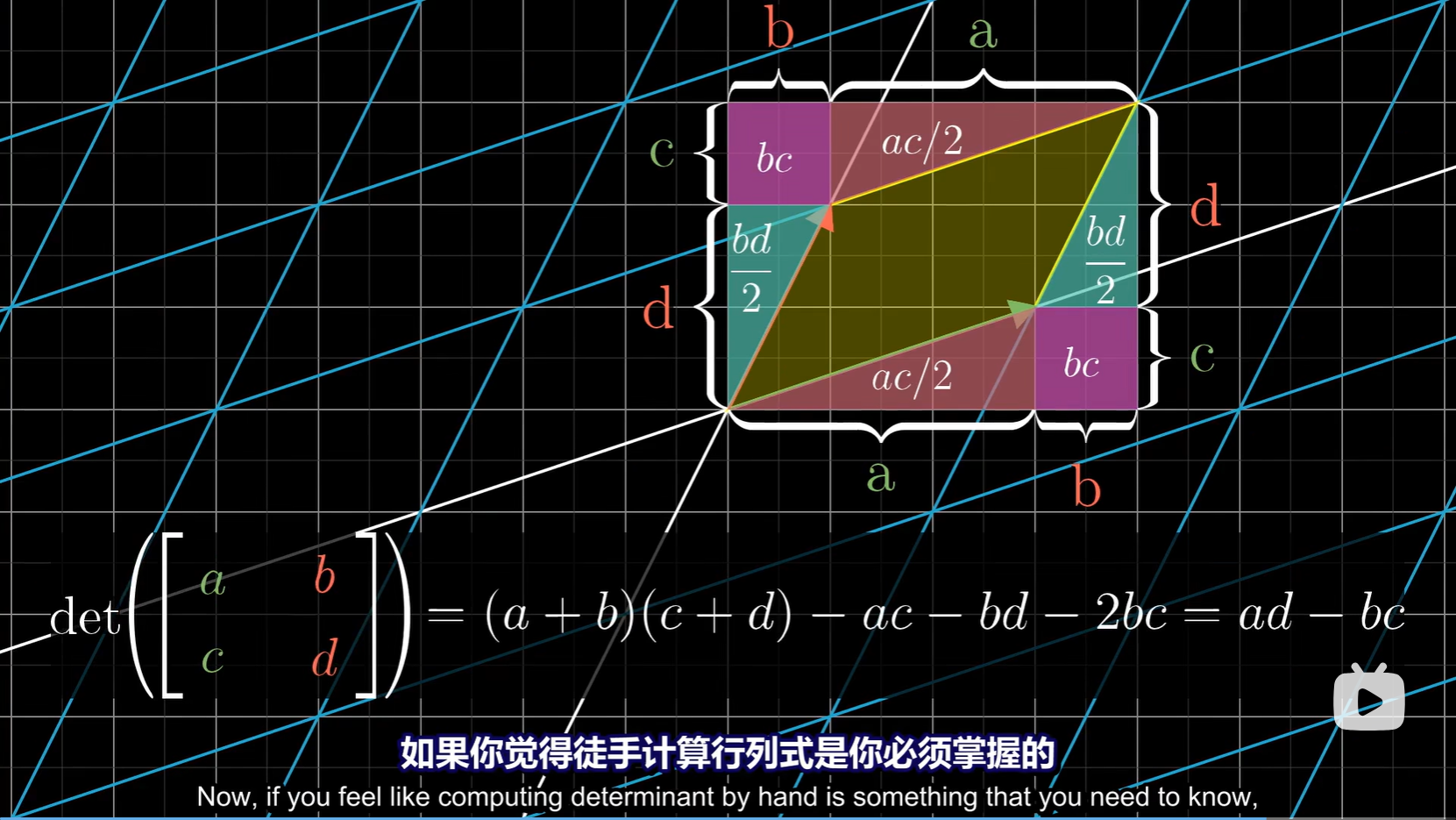

\(det(M_1)\) , \(det(M_2)\) 都代表缩放的倍率,倍率可以相乘
逆矩阵,列空间,零空间
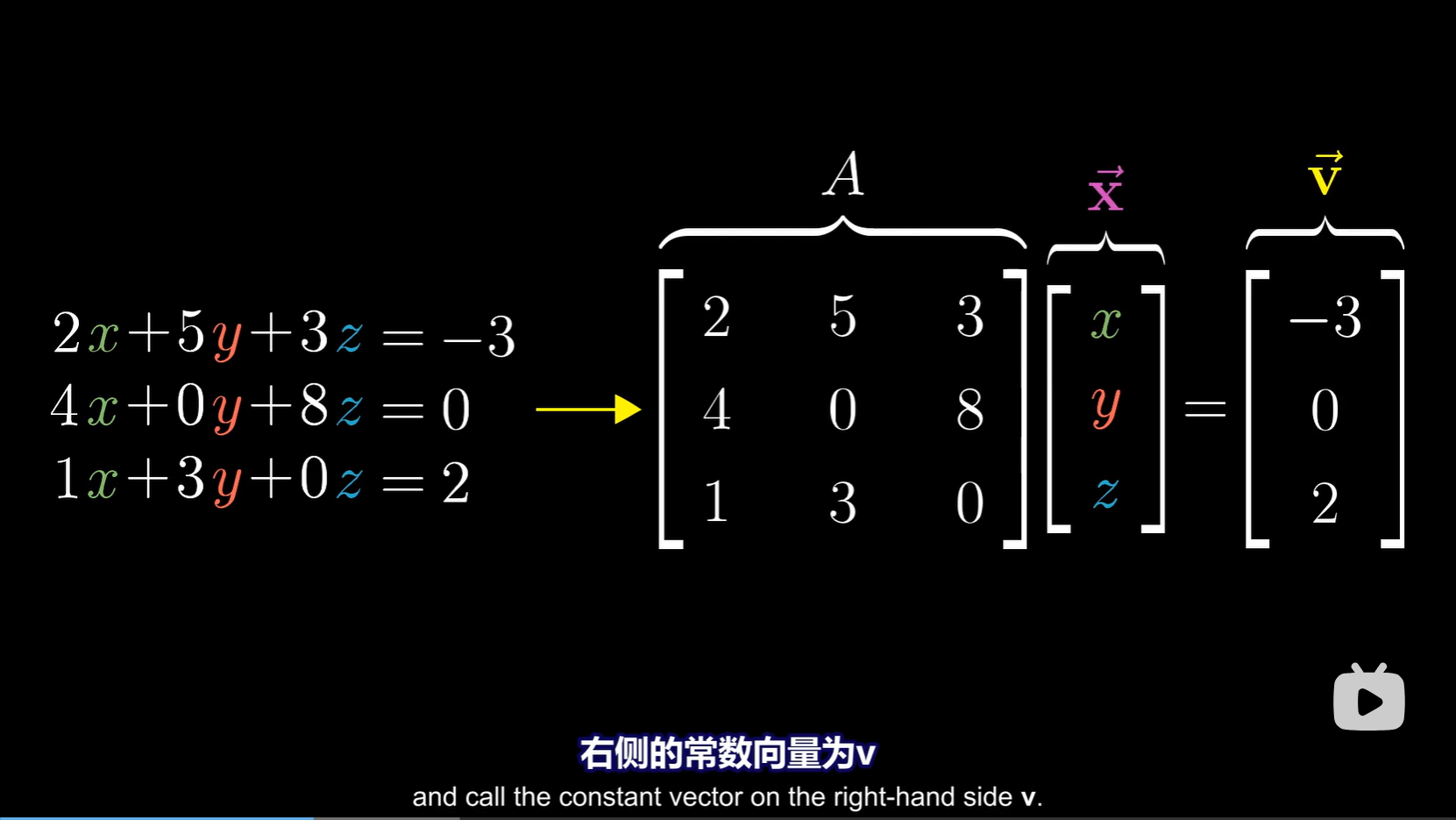
让我们看看矩阵在方程组里面有什么更加直观的解释
上式可以看成找到一个 \(\vec{x}\) 使得它在经过线性变换A之后变为 \(\vec{v}\)

矩阵的逆
一个矩阵的逆矩阵就是把这种变换逆回去
这样我们就可以在等式的两边同时乘以\(A^{-1}\)来求解\(\vec{x}\)
在这里当\(det(A)=0\)时,不存在\(A^{-1}\),直观上讲一条直线不能还原成一个平面,有无数个向量会压缩到这条直线上,但是一条直线不能还原为无数条向量,这其实对应着函数的性质。但即使\(det(A)=0\),也可能存在解

在这里,我们用 秩 来表示一个空间在经过线性变换后剩余的维度,它可以用来表示原本的空间被压缩的程度(三维压缩成二维,三维被压缩成一维...)
在经过A线性变换的空间或者说基向量张成的空间就是A的列空间,那么A的秩就是列空间的维度
经过线性变换之后落在远点的向量集合称为A的零空间或核

注意,线性变换的矩阵大多都是方阵,对于非方阵的线性变换,这种变换会使空间扩张或压缩,同时导致该变换矩阵没有行列式以及逆矩阵等性质
不过非方阵是有秩的,行秩和列秩是相等的
点积与对偶性
这一小节我们来看看如何在线性变换中解释点积
虽然非方阵的线性变化会改变空间的维数,导致这个矩阵失去一些意义,但是压缩矩阵(将任意维数的空间压缩成一维)刚好可以解释点积
我们可以用 投影 来定义从任意维数压缩成一维的线性变换,直观来看,投影这种操作是满足线性变换的要求的,那么这时我们的变换矩阵就是个1*n的向量
在这个过程中追踪每一个向量在转换后的位置(一维坐标),也就是求投影的坐标,就是通过矩阵乘法实现的!

以线性变换的角度看叉积
叉积可以用来表示两个向量围成的平行四边形的面积(大小是一样的)
........
基变换
之前的变换大多都是从直角坐标系出发,旋转,拉伸这个坐标系(空间),得到了另一个坐标系(空间),然后我们寻找原来的某个向量经过这种变换之后在原来的坐标系中的位置, 这个时候我们仍然用原来的坐标系去判断其他向量的位置,但是我们没有探讨经过旋转,拉伸得到的这个新的坐标系(空间)的性质。
 |
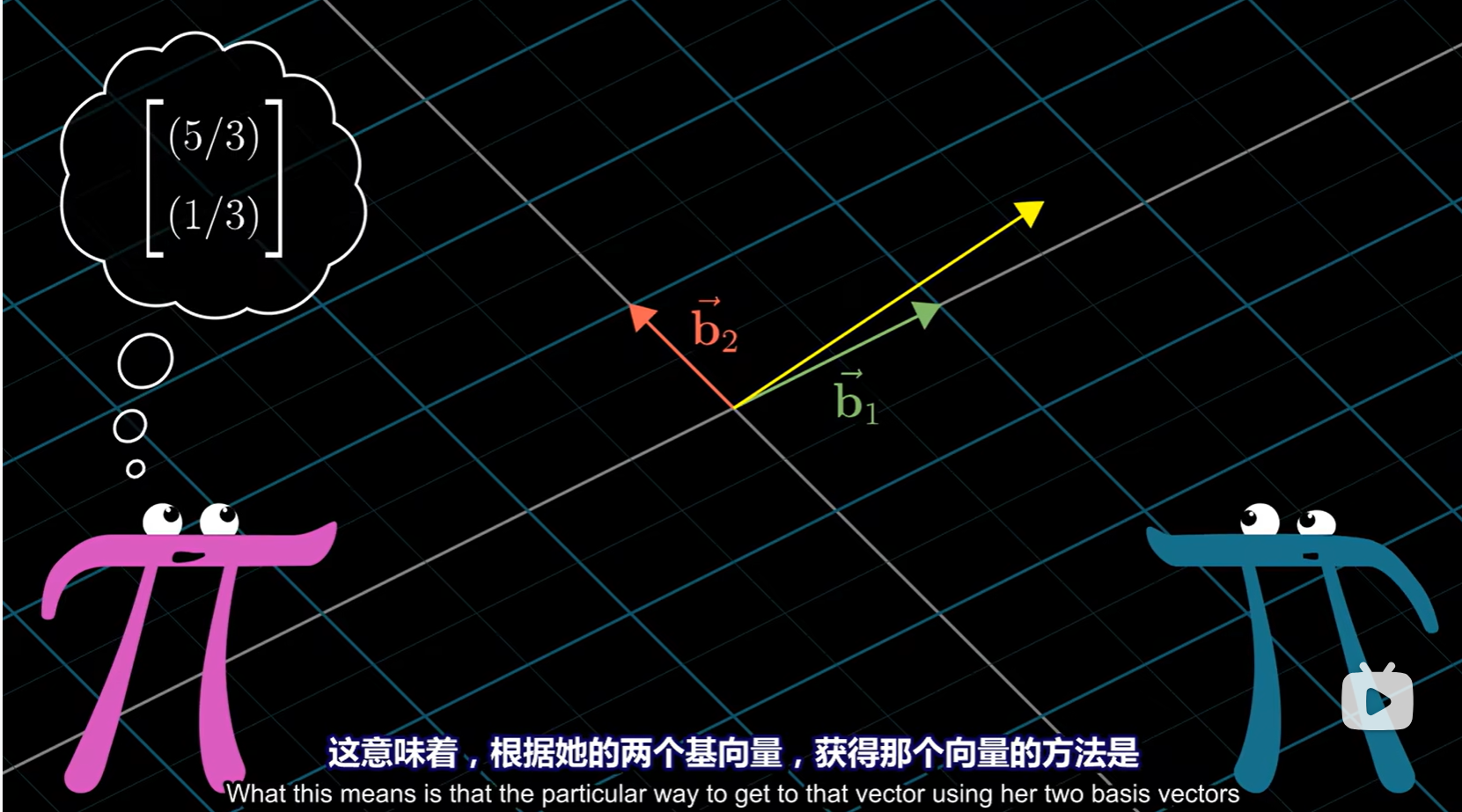 |
左边是我们常用的坐标系,我们用M代称,右边是一个新的,区别于直角坐标系的坐标系,我们用N代称
在两个坐标系中,我们都选择[1, 0], [0, 1]作为基向量,由于坐标系不同,这两对基向量在客观空间上也不同,那么即使对同一个向量(黄色),在两个坐标系中用相同的基向量表示方法也不同
这里可以将M,N理解成两种语言,及时它们描述的是客观空间中的同一个向量,但展现出来的数值却不同

对于这个黄色的向量,我们给他两个名字\(\vec{x_M}\)是在M中的名字(坐标),\(\vec{x_N}\)是在N中的名字(坐标)
那么如果我们知道了在N中这个向量的名字(位置),我们如何知道在M中这个向量在哪呢(坐标)?
我们只需要知道N中的基向量(\(\vec{b_1}\), \(\vec{b_2}\))在M中的位置即可,而这恰好就是从M到N的变换矩阵,我们称之为\(A\),那么\(A\vec{x_N}\)就是这个向量在M中的位置
相反,如果我们知道在M中这个向量的名字(位置),我们如何知道在N中这个向量在哪?
同理,我们只用知道从N到M的变换矩阵,称之为B(注意这个矩阵表示的是在N中,M的基向量\(\vec{i}, \vec{j}\)的位置),那么\(B\vec{x_M}\)就是答案
注意, 这里的\(A, B\)互为 逆矩阵 (视频里没解释,我也懒得找证明,就直观的感受一下吧......)
这个矩阵其实就充当着不同语言(坐标系)中的翻译功能
\[A\vec{x_N} = \vec{x_M}\\ \vec{x_N} = A^{-1}\vec{x_M} \]我们现在考虑一个旋转90°的矩阵,在直角坐标系下,它为[[0, -1], [1, 0]],但是如果直接将这个矩阵应用于其他坐标系,旋转大概率不是90°,而是另一个坐标系中两个轴的夹角。那我们如何求得在另一个坐标系中的旋转矩阵呢?
- 任意在新的坐标系下取一个坐标\(\vec{v}\),获得它在直角坐标系下的坐标\(A\vec{v}\)
- 把这个坐标在直角坐标系下旋转,\(MA\vec{v}\),这里的M就是上面的旋转矩阵
- 在将得到的坐标转化为新坐标系下的坐标,\(A^{-1}MA\vec{v}\)
由于\(\vec{v}\)是任意取的,所以新坐标系下的旋转矩阵为\(A^{-1}MA\),所以想这么个东西其实暗含着在不同视角下的同一个变换
特征向量与特征值
在一个线性变换A中,大部分向量都发生了偏移,但少部分向量不会移动,只是被拉伸了,这样的向量称为A的特征向量,拉伸的倍数就是A的特征值
在三维空间中特征向量会更直观,由于线性变换不会移动原点,那么这个过程中不偏移的向量就是三维空间旋转的旋转轴
\[A\vec{v} = \lambda\vec{v} \]从特征向量的公式可以看出,特征向量就是在变换的过程中仅仅被拉伸的向量
对上式等价变化一下
\[(A-\lambda I)\vec{v}=0 \]只有当\(det(A-\lambda I)\)为0时,这个世子才有解。
标签:线性变换,3b1b,变换,矩阵,本质,vec,线代,坐标系,向量 From: https://www.cnblogs.com/hetailang/p/18449130