力学笔记

标签：frac 无滑 2Fx 笔记 mv 力学 alpha aligned

无滑滚动

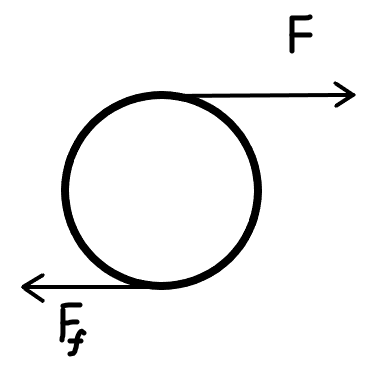
假设有拉力\(F\)以及摩擦力\(F_f\)，圆柱体无滑滚动（\(a=\alpha R\)），下面讨论其动能变化

由质心运动定理：

\[F-F_f=ma \]

由刚体定轴转动的转动定理：

\[(F+F_f)R=I_c\alpha \]

可得：

\[a=\frac{2F}{m+\frac{I_c}{R^2}} \]

故刚体动能为：

\[\begin{aligned} E_k&=\frac{1}{2}mv^2+\frac{1}{2}I_c\omega^2\\ &=\frac{1}{2}mv^2+\frac{1}{2}I_c\frac{v^2}{E^2}\\ &=\frac{1}{2}(m+\frac{I_c}{R^2})v^2\\ &=(m+\frac{I_c}{R^2})ax\\ &=2Fx\\ \end{aligned}\]

为何\(E_k=2Fx\)而不是\(Fx\)呢？

由于\(a=\alpha R\)，故\(F\)的作用点速度为质心速度的两倍，位移也为两倍

标签：frac,无滑,2Fx,笔记,mv,力学,alpha,aligned
From： https://www.cnblogs.com/Grice/p/18150739