莫比乌斯反演
-
考虑狄利克雷前缀和的式子,\(g(n)=\sum\limits_{d\mid n} f(d)\)。
-
知 \(f\) 求 \(g\) 是 naive 的;知 \(g\) 求 \(f\) 呢?
-
首先上式等价于 \(g=f\ast I\),若我们有 \(inv_I\),则有 \(f=g\ast inv_I\)。
-
求 \(inv_I\),得到 \(\mu\),于是 \(f=g\ast \mu\),即 \(f(n)=\sum\limits_{d\mid n} \mu(d)g(\frac{n}{d})\)。
-
该式称为莫比乌斯反演,即对积卷积过程的反演。事实上,我们称 \(g\) 是 \(f\) 的莫比乌斯变换,\(f\) 是 \(g\) 的莫比乌斯逆变换(反演)。
-
特别地,当 \(g=id,f=\varphi\),也称为欧拉反演。欧拉反演的应用比较狭窄,但有时比 \(\mu\ast I=\epsilon\) 的方法要简洁有力得多。
-
所谓反演,就是已知 \(f,g\) 的某种关系,通常是容易 \(f\to g\) 的,要求逆向求出 \(f\) 关于 \(g\) 的表达式。
-
“反演的本质是将逻辑表达式改换成代数式,从而使其可以参与代数运算,为化式子提供机会”,这是我的某个前辈对反演的评价。
-
在莫反中,其的表现主要是将 \(\sum\limits_d\) 交换到前面,于是原本在前的和式变成了。(以 \(\sum\limits_{i=1}^n f(i)\sum\limits_{d\mid i}\) 为例)形如 \(\sum\limits_{i=kd}^nf(i)\) 也即只在 \(d\) 的倍数处求和的和式,于是可以和整除分块相结合或者便于进一步化式子。
-
既然提到了,那么也把整除分块放在这里。
整除分块
- 考虑求 \(\sum\limits_{i=1}^n \lfloor\frac{n}{i}\rfloor\)。
引理:\(\forall a,b,c\in \mathbb{Z},\lfloor\frac{a}{bc}\rfloor=\lfloor\dfrac{\lfloor\frac{a}{b}\rfloor}{c}\rfloor\)。
- 不妨设 \(\frac{a}{b}=k+r\),其中 \(k\in \mathbb{Z},r\in [0,1)\),于是
- 这里我们设 \(k=k'c+r'\),其中 \(k',r'\in \mathbb{Z}\),且 \(r'\in [0,c)\),于是
- 注意到 \(r'<c\to c-r'\geqslant 1\),但 \(r<1\to \frac{r}{c}<1\),所以 \(r'+\frac{r}{c}<1\),于是
- 证毕。
定理 1:\(\lfloor\frac{n}{i}\rfloor\) 只有 \(O(\sqrt{n})\) 种不同取值。
-
记 \(sq=\lceil\sqrt{n}\rceil\)。
-
\(\forall i\leqslant sq\),\(i\) 只有 \(O(\sqrt{n})\) 种,显然 \(\lfloor\frac{n}{i}\rfloor\) 也只有 \(O(\sqrt{n})\) 种。
-
\(\forall i>sq\),\(\lfloor\frac{n}{i}\rfloor\leqslant sq\),于是 \(\lfloor\frac{n}{i}\rfloor\) 还是只有 \(O(\sqrt{n})\) 种。
-
故 \(\lfloor\frac{n}{i}\rfloor\) 只有 \(O(\sqrt{n})\) 种取值,表现大概是这样
-
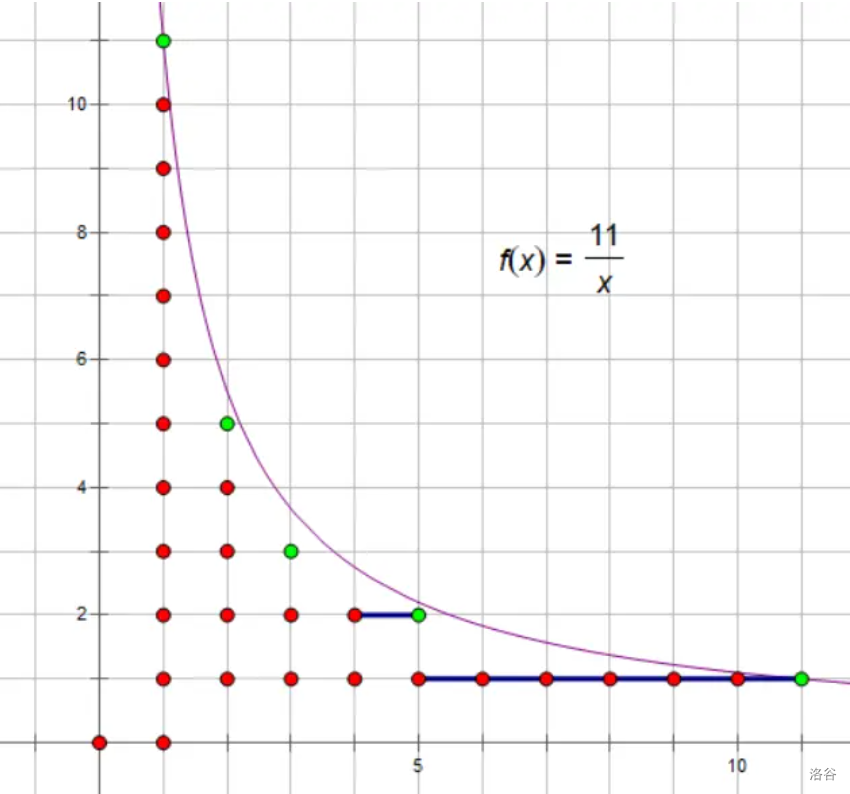
定理 2:\(\forall \lfloor\frac{n}{j}\rfloor=\lfloor\frac{n}{i}\rfloor,j_{\max}=\lfloor\dfrac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\)。
- 不妨设 \(n=ki+r\),即 \(k=\lfloor\frac{n}{i}\rfloor\),于是有
-
换言之,\(\forall \lfloor\frac{n}{j}\rfloor=\lfloor\frac{n}{i}\rfloor,\lfloor\frac{n}{k}\rfloor \geqslant j\),故 \(\lfloor\frac{n}{k}\rfloor=\lfloor\dfrac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor=j_{\max}\)。
-
当然我们还要证明 \(\lfloor\frac{n}{k}\rfloor\) 是一个合法的 \(j\),即 \(\lfloor\dfrac{n}{\lfloor\frac{n}{k}\rfloor}\rfloor=\lfloor\frac{n}{i}\rfloor\)。
-
将式子展开,得到
- 考虑拆掉最里层的 \(\lfloor\rfloor\),发现 \(\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\to \lfloor\frac{n}{\frac{n}{i}}\rfloor=\lfloor i \rfloor=i\) 是变小了,分母变小整体变大,故有
- 考虑拆掉中间层的 \(\lfloor\rfloor\),发现分母变大整体变小,式子变为
- 就是说,有
- 联立,得到
-
所以 \(\lfloor\dfrac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\) 既是最大的,又是合法的,所以它是段 \(\lfloor\frac{n}{i}\rfloor\) 的右端点。
-
总之,整除分块可以用来快速求和。其也可以推广到多维,即 \(\sum\limits_{i=1}^{\min_{j=1}^{m} n_j} \prod\limits_{j=1}^m \lfloor\dfrac{n_j}{i}\rfloor\)。
-
可以发现此时不同的 \(\prod\) 值只有 \(O(\sqrt{n}m)\) 种,因为对于左边界 \(l\),右边界为 \(\min_{j=1}^m \lfloor\dfrac{n_j}{\lfloor\frac{n_j}{l}\rfloor}\rfloor\),表现大概是这样:
-
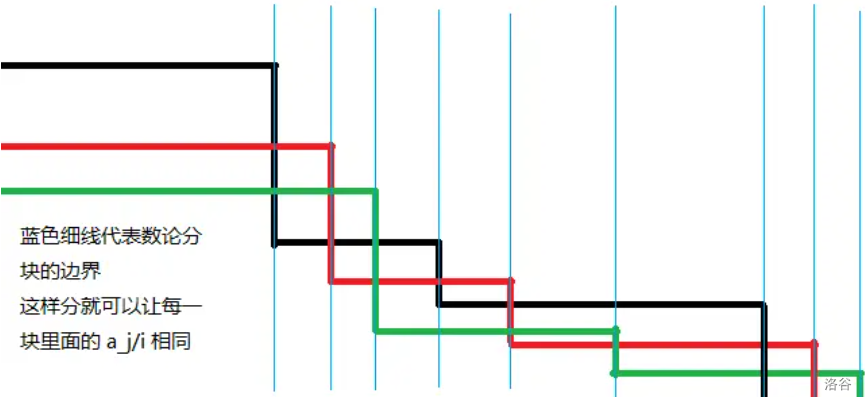
例题
P1447 [NOI2010] 能量采集
-
题意略。“太经典了,我每年都要讲”。
-
手推+感性理解,很快发现 \((i,j)\) 是对应直线上的第 \(gcd(i,j)\) 个,造成 \(2gcd(i,j)-1\) 的能量损失。
-
于是所求的答案可以做如下转换,这里认为 \(n\leqslant m\):
-
若我们能快速求得 \(res\),则 \(ans=2res-nm\)。
-
然后有一个经典的容斥:记 \(f(d)=\sum\limits_{i=1}^n \sum\limits_{j=1}^m [gcd(i,j)=d]\),\(g(d)=\sum\limits_{i=1}^n \sum\limits_{j=1}^m [d\mid gcd(i,j)]\),我们有
-
显然 \(g\) 可以 \(O(n)\) 地求得,但求 \(f\) 的过程是 \(O(n\ln n)\) 的。过原题够了,但若 \(n,m\leqslant 10^7\) 呢?
-
这个容斥式子没啥希望了,它的形态就不优美,\(kd\)...我们转而考虑狄利克雷卷积和莫比乌斯反演。接着上面的式子推,我们有
-
事实上,到这一步,我们已经可以 \(O(n)\) 地求出答案了。对内部式子使用整除分块,乍一看复杂度是 \(O(n\sqrt{n})\),实际上复杂度应为 \(\sum\limits_{d=1}^n \sqrt{\lfloor\frac{n}{d}\rfloor}\),可以积分分析到 \(O(n)\)。
-
考虑多测,\(T\leqslant 10^5\)。那就继续化!发现这里我们每次都要重新整除分块,设法把这部分提出来。
-
线性筛 \(\varphi\) 的前缀和,然后整除分块,复杂度 \(O(n+T\sqrt{n})\)。
-
事实上,我们可以使用欧拉反演:
- 简洁有力...不要忘记尝试欧拉反演。
P3312 [SDOI2014] 数表
-
题意:多测,求 \(\sum\limits_{i=1}^n \sum\limits_{j=1}^m [\sigma_0(gcd(i,j))\leqslant x]\times \sigma_0(gcd(i,j))\)。
-
首先我们把 \(\sigma_0\) 筛出来,然后化式子,还是认为 \(n\leqslant m\):
- 很套路地卷一个 \(\epsilon\),快进到
-
发现这里化不下去,\(d=id\) 的美妙性质在这里没有了,还有一个恶心的逻辑表达式。
-
考虑将所有数字按 \(\sigma_0\) 排序,定义一个函数
-
问题变成求 \(f\) 的前缀和,考虑离线询问(我们做一个贡献法),按 \(a\) 升序排序,每次让 \(d\) 对所有 \(f(td)\) 贡献。
-
既然 \(d\) 只会被扫到一次,那么此部分的总复杂度应为 \(O(n\ln n)\),\(\mu\) 可以线筛预处理,此时问题变成有多组询问,求
- 那么这就是一个很板的整除分块了。注意到 \(f\) 需要单点修改和区间查询,考虑使用树状数组维护之,于是总复杂度为 \(O(n\log^2+q\sqrt{n}\log)\),两部分分别是修改和查询的复杂度。
P2522 [HAOI2011] Problem b
-
题意:求 \(\sum\limits_{i=a}^b \sum\limits_{j=c}^d [gcd(i,j)=d]\),多测。
-
首先我们做一个二维差分,所求变成:
- 卷 \(\epsilon\),快进:
-
整除分块之,\(O(n+T\sqrt{n})\)。
-
显然这两道题上欧拉反演都无用武之地,可见欧拉反演虽然简洁,却也局限,应用范围非常狭窄。
P2424 约数和
-
题意:求 \(\sum\limits_{i=l}^r \sigma_0(i)\)。
-
数据范围:\(l,r\leqslant 2\times 10^9\)。
-
首先容易想到 \(\sigma_0=I\ast id\to \sigma_0\ast \mu=id\),于是可以杜。
-
但本题只有单组询问,我们考虑直接莫反:
- 结束,\(O(\sqrt{n})\)。