定义一个形如 \(x=a+bi\) 的数为复数。
上式中的 \(i\) 为虚数单位,有 \(i\cdot i=-1\)。
-
两个复数 \(x\) 和 \(y\) 相等,当且仅当 \(x_a=y_a\) 且 \(x_b=y_b\)。
-
对于一个复数 \(x\),我们称 \(a\) 为 \(x\) 的实部,\(b\) 为 \(x\) 的虚部。
-
当 \(a=0\) 时,称 \(x\) 为纯虚数。
-
容易发现,复数可以用数对 \((a,b)\) 的形式表现出来。若将 \((a,b)\) 看作平面直角坐标系上的一个点,全体复数可以一一对应。
-
将平面直角坐标系的横坐标视为实部,纵坐标视为虚部,此时这个具有与复数一一对应关系的平面叫做复平面。
- 定义复数 \(x=a_1+b_1i\) 和 \(y=a_2+b_2i\) 的加法。
容易证明,复数加法满足交换律。
- 定义复数 \(x=a_1+b_1i\) 和 \(y=a_2+b_2i\) 的乘法。
容易证明,复数乘法满足交换律。
记 \(-x=(-1)\cdot x\),因此 \(x-y=x+(-1)\cdot y\)。
具体的,令复数 \(z=a+bi\),其中 \(a=-1,b=0\),那么就有了如下的定义。
- 定义复数 \(x=a_1+b_1i\) 和 \(y=a_2+b_2i\) 的减法。
容易发现,复数的加减法就和以下一个过程相同。
在复平面上,原点 \((0,0)\) 和 \((a_1,b_1)\) 表示的数 \(x\) 构成一个向量 \(\vec{A}\)。
同理,原点 \((0,0)\) 和 \((a_2,b_2)\) 表示的数 \(y\) 构成一个向量 \(\vec{B}\)。
我们对向量 \(\vec{A}\) 和 \(\vec{B}\) 作向量加减法。
用较为严谨的语言表示:
复数加减法与复平面上的向量加减法相对应。
定义一个复数 \(x\) 的 模长 \(|x|\) 为其实部与虚部的平方之和的算术平方根(其实就是复平面上点 \(x\) 到原点的欧几里得距离)。
形式化来说,
\[|x|=\sqrt{a^2+b^2} \]定义复数 \(x\) 和 \(y\) 的 距离 \(d(x,y)=|x-y|\),可以发现以下性质。
- \(d(x,y)\ge 0\),当 \(d(x,y)=0\) 时,\(x=y\)。
- \(d(x,y)=d(y,x)\)。
- \(d(x,y)+d(x,z)>d(y,z)\)。
我们称满足以上三个性质的 \((\mathbb{C},d)\) 为一个 度量空间。
容易证明,\(|x\cdot y|=|x|\cdot |y|\)。
复数 \(x=a+bi\) 可以被表示为 \(r(\cos\theta+\sin\theta \cdot i)\) 的形式,且表示方法唯一。
我们将这样的表示方法称为 三角表示。
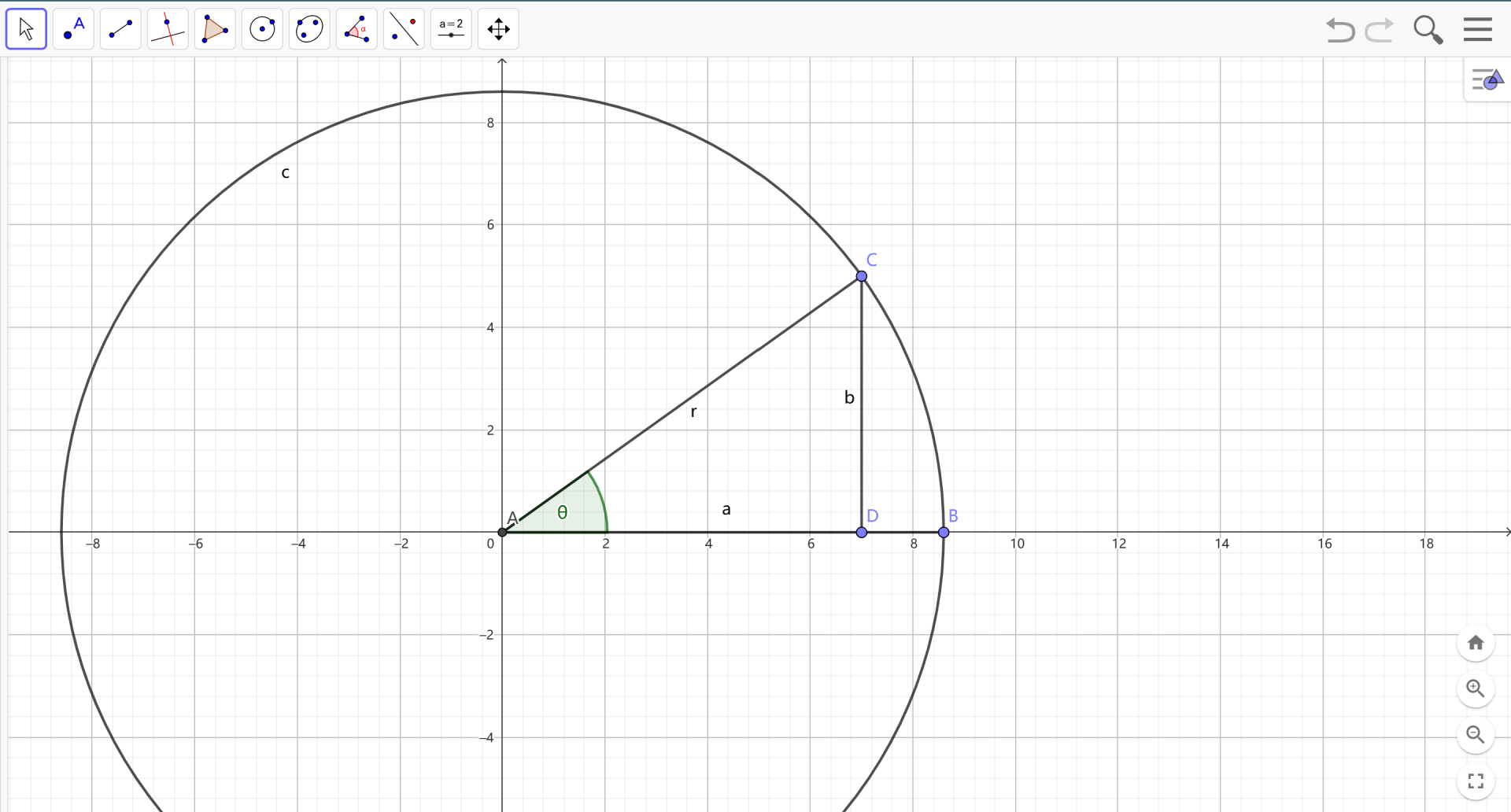
上图为复数 \(x=a+b_i\) 在复平面上的三角表示。
其中,\(r\) 即为 \(x\) 的 模长。
定义上图中的角度 \(\theta\) 为 \(x\) 的 幅角。容易发现,\(x\) 的幅角有无限个,但在 \(\left ( -\pi ,\pi \right ]\) 的范围内只有一个。将这个唯一的值称为 幅角主值,表示为 \(\theta=\arg(x)\)。
设复数 \(x=r_1(\cos\theta_1+\sin\theta_1\cdot i)\),\(y=r_2(\cos\theta_2+\sin\theta_2\cdot i)\)。
有:
\[\begin{aligned} xy&=r_1r_2(\cos\theta_1+\sin\theta_1\cdot i)(\cos\theta_2+\sin\theta_2\cdot i)\\ &=r_1r_2[(\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2)+(\sin\theta_1\cos\theta_2+\cos\theta_1\sin\theta_2)]\\ &=r_1r_2[\cos(\theta_1+\theta_2)+\sin(\theta_1+\theta_2)\cdot i] \end{aligned} \]由于复数的乘法和除法互为逆运算,故两个复数之商(第二个复数非零)的模长为两个复数模长之商,辐角为两个复数辐角之差。
标签:cos,cdot,笔记,数学,复数,平面,theta,sin From: https://www.cnblogs.com/zxcqwq/p/18678982