让我们从基础概念开始。我们将要把欧式平面拓展为实射影平面。
我们约定平行线交于无穷远点。不同方向的平行线交于不同的无穷远点,所有无穷远点都在无穷远直线上
在这样的定义下,依然有两点确定一条直线。对于无穷远点,可以简单地理解为一个方向,将它与某个点相连,就是过这个点做某一个方向的直线。
对共线四点 \(A,B,X,Y\) ,定义交比为(线段是有向的)
\((A,B;X,Y)=\frac {XA}{XB}\div \frac{YA}{YB}\)
对共点直线 \(a,b,x,y\) 定义交比为(角度是有向的,不过更直观的理解是若 \(x,y\) 夹在 \(a,b\) 之间(四个角的一个)为负,否则为正)
\((a,b;x,y)=\frac{\sin<x,a>}{sin<x,b>}\div \frac{\sin<y,a>}{\sin<y,b>}\)
记 \(P(A,B;X,Y)=(PA,PB;PX,PY)\)
定理 \(1\) :对平面上任一点 \(P\) 与共线四点 \(A,B,X,Y\) 有:
\((A,B;X,Y)=P(A,B;X,Y)\)
直接代入定义即可验证,这个定理给出的重要事实是,可以将 \(A,B,X,Y\) 通过 \(P\) 透视到另一条直线上,不改变交比
定理 \(2\) :对圆上五点 \(P,A,B,X,Y\) ,有:
\(P(A,B;X,Y)=\pm \frac{XA}{XB}\div\frac {YA}{YB}\)
若线段 \(AB,XY\) 不相交为正,否则为负
不难由圆周角与弦的关系得到
上述两个性质可以实现将一条直线(或一个圆)上的四个点透视到另一条直线(或一个圆)上,这是射影几何最为关键的方法之一
由交比的透视性质,我们引入射影变换:
通过一个点,将一个平面的点透视到另一个平面上,称为射影变换。
我们不深入探究其性质与相关证明,只是说它具有这样的性质:
定理 \(3\) :在任意射影变换下:
-
直线对应直线
-
二次曲线对应二次曲线
-
交比不变
-
任意直线曲线的交点数不变(特别地,相切性保持)
射影变换的主要功力在下:
定理 \(4\) :可以通过射影变换实现以下操作:
-
将平面上四点变为其它任四点
-
维持平面上一个二次曲线的形状(上面的点发生了改变!),使其内部一个点变为其内部另一个点
-
维持平面上一个二次曲线的形状,将与曲线相离的直线变为无穷远直线
例1
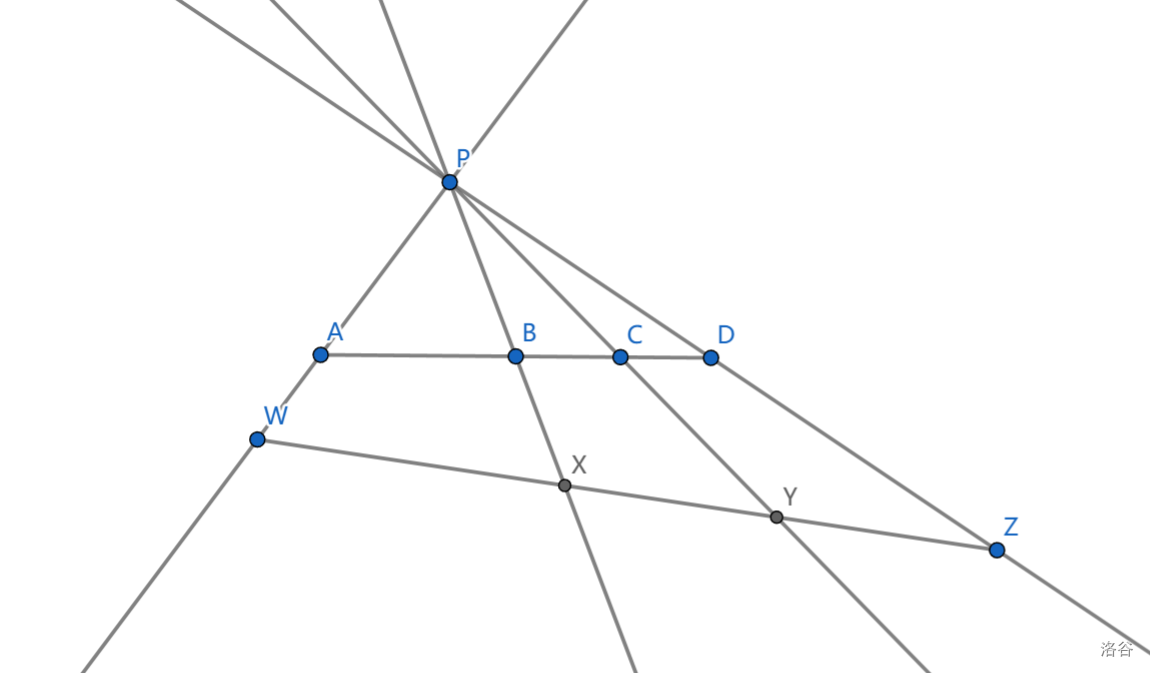
(笛沙格定理)对 \(\triangle ABC,\triangle XYZ\) ,若 \(AX,BY,CZ\) 共点,称它们关于其交点透视,若 \(AB\cap XY,AC\cap XZ,BC\cap YZ\) 共线,称它们关于这条直线透视。证明:两三角形关于某点透视当且仅当它们关于某直线透视
利用射影变换,将 \(ABXY\) 变为正方形,设 \(M=CA\cap ZX,N=CB\cap YZ\) ,另一个交点是无穷远点
现在只要证 \(NM//AB\iff CZ//AX\)
\(CZ//AX\rightarrow\frac{NB}{BC}=\frac{BY}{CZ}=\frac{AX}{CZ}=\frac{MA}{AC}\rightarrow NM//AB\)
\(NM//AB\rightarrow \frac{CA}{AM}=\frac{AB}{NM}=\frac{XY}{NM}=\frac{XZ}{MX}\rightarrow CZ//AX\)
证毕。
例2
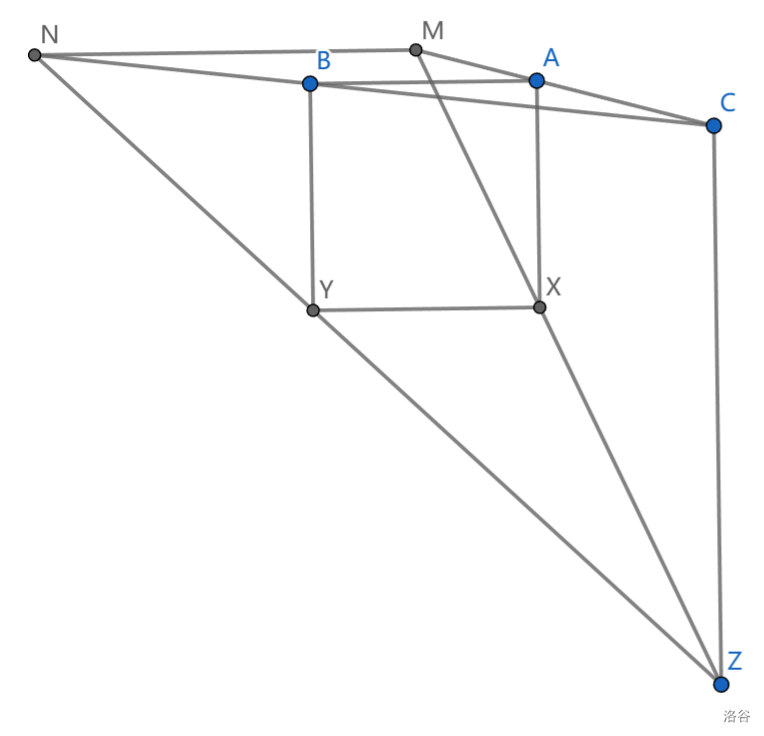
给定一个圆 \(c\) 以及圆外两点 \(P,Q\) ,满足直线 \(PQ\) 与 \(c\) 相离。定义映射 \(f:c\rightarrow c\) 如下:连接 \(XP\) 交 \(c\) 于 \(Y\) ,连接 \(YQ\) 交 \(c\) 于 \(Z\) ,则 \(f(X)=Z\) 。证明:若 \(f\) 存在一个 \(n\) 阶不动点,则 \(f^{(n)}=id\)
将 \(PQ\) 变为无穷远直线,则 \(XY//l_P,YZ//l_Q\) (其中 \(l_P,l_Q\) 是 \(P,Q\) 的方向,即两条定直线),那么 \(\angle XOZ\) 为定值 \(2<l_P,l_Q>\) ,即 \(f\) 为旋转变换,证毕。
(可能有人问为什么要先讲射影变换,其实是因为笔者懒得用梅涅劳斯和相似来证明以下的一些定理罢了,这些证明可以在任何一本几何书内查阅到)
我们回归主题。我们特别关注 \((A,B;X,Y)=-1\) 的情况,称这类 \((A,B;X,Y)\) 为调和点列。 我们还称对边乘积相等的圆内接四边形为调和四边形(显然这样的四边形满足 \(P(A,B;C,D)=-1\) , \(P\) 是 \(\odot(ABCD)\) 上任一点)
对于某个圆 \(O\) ,设 \(X,X'\) 是关于它的反演对应点,则过 \(X'\) 且垂直于 \(OX'\) 的直线 \(l\) 被称为 \(X\) 关于圆的极线, \(X\) 是 \(l\) 的极点
定理 \(4\) :有下列较为显然的事实:
-
\((A,B;X,Y)=(X,Y;A,B)\)
-
\((A,B;M,P_\infty)=-1\) ,其中 \(M\) 为 \(AB\) 中点
第 \(2\) 点给出了一个处理中点与平行线的手法,我们稍后会在例题看到(因为平行线交于 \(P_\infty\) )
定理 \(5\) :设 \(\omega\) 为圆,圆上有四边形 \(AXBY\) ,定义 \(Q=AB\cap XY\) ,则下列命题等价:
-
\(AXBY\) 是调和四边形
-
\(AB\) 是 \(\triangle AXY\) 的共轭中线
-
\(A,B,P\) 共线,其中 \(P\) 是 \(XY\) 的极点
并且上述条件下, \((A,B;Q,P)=-1\) (极线中的调和点列)
证明:将 \(Q\) 射影变换为圆心并保持 \(\omega\) 不变 ,若其为调和四边形则必为正方形,三个命题显然等价
而 \((A,B;Q,P)\) 是从 \(X\) 将调和四边形 \(AXBY\) 透视到 \(AB\) 的结果( \(XX\) 即过 \(X\) 的切线)
我们将引入更多常见的调和点列:
定理 \(6\) :设 \(\triangle ABC\) 内 \(AD,BE,CF\) 交于一点 \(P\) ,记 \(X=EF\cap BC\) ,则 \((C,B;D,X)=-1\) ,设 \(Y=AD\cap EF\) ,通过透视即可得到 \((E,F;X,Y)=-1\)
证明:将 \(P\) 射影变换至重心,维持 \(A,B,C\) 不变,由定理 \(4\) 完成证明。
也可以表述为完全四边形 \(BCEF\) 中的调和点列,这是完全四边形中最重要的定理之一。
定理 \(7\) :设 \(X,A,Y,B\) 依次排列在一条直线上, \(C\) 是直线外一点,则下列三个条件可以由两个推出第三个:
-
\((A,B;X,Y)=-1\)
-
\(\angle XCY=Rt\angle\)
-
\(CX\) 是 \(\angle ACB\) 的角平分线
此定理的重述即阿波罗尼斯圆:对给定点 \(A,B\) 与常数 \(k\) ,满足 \(AC/BC=k\) 的点位于一个圆上(该圆与 \(AB\) 的交点即定理中的 \(X,Y\) )
证明:在直线 \(AB\) 上取点 \(X,Y\) 满足 \(XA/XB=YA/YB=k\)
取 \(XY\) 的中点 \(M\) ,则 \(\triangle MAC\sim \triangle MCB\) ,给出 \(MC=\sqrt{MA\cdot MB}\) 为定值,证毕
上述证明过程给出了一个重要的调和点列性质:我们过 \(B\) 作阿氏圆的切线 \(BC\) ,则由 \(\triangle MAC\sim \triangle MCB\) 给出 \(A\) 是 \(Rt\triangle BMC\) 的斜边垂足,由射影定理直接得到:
定理 \(8\) :对调和点列 \((A,B;X,Y)=-1\) 及 \(XY\) 中点 \(M\) ,有 \(MX^2=MA\cdot MB\)
(很多书籍要求读者通过代数方法验证这条性质。我们在此对这类误人子弟的书籍表示强烈的谴责。)
这个定理结合高斯线(国内称作牛顿线)很有用,也可以很好地处理中点,将在稍后例题展示。
最后还有两个重要的关于极点极线的定理。以下默认用 \(l_X\) 表示 \(X\) 的极线
定理 \(9\) :若 \(Q\in l_P\) ,则 \(P\in l_Q\) ,称 \(P,Q\) 关于圆共轭
证明: 设 \(P\) 的反演对应点(也就是 \(P\) 的极线与 \(OP\) 的交点)是 \(P'\) ,利用等差幂线,有
\(PQ^2-OQ^2=PP'^2-OP'^2=OP(OP-2OP')=OP^2-2R^2\)
从而 \(Q\in l_P\iff PQ^2=OP^2+OQ^2-2R^2\) ,这是对称的,证毕
解析方法的好处是它直接给出了推论 \(9.1\) : \(P,Q\) 关于 \(\Gamma\) 共轭 \(\iff \odot(直径PQ),\Gamma\) 正交
显然的推论 \(9.2\) :
设 \(P=l_A\cap l_B\) ,则 \(l_P=AB\)
这更多是一种分析思想,可以转换三点共线与三线共点问题。
推论 \(9.3\) :设 \(A,B,C,D\) 在圆上, \(S,T\) 是 \(AB,CD\) 的极点,并设 \(AC\cap BD=K\) ,则 \(K,S,T\) 共线
证明:设 \(AB\cap CD=X\) ,根据推论 \(9.2\) , \(l_X=ST\) ,但根据 \(Brocard\) 定理, \(K\) 也在 \(X\) 极线上。
定理 \(10\) : (\(Brocard\) 定理)对圆上四点 \(A,B,C,D\) ,若 \(AB\cap CD=X,AC\cap BD=Y,AD\cap BC=Z\) ,则 \(l_X=YZ,l_Y=XZ,l_Z=XY\) ,并且 \(\triangle XYZ\) 的垂心是圆心 \(O\)
下面的例题展示了基础的透视方法。
例3
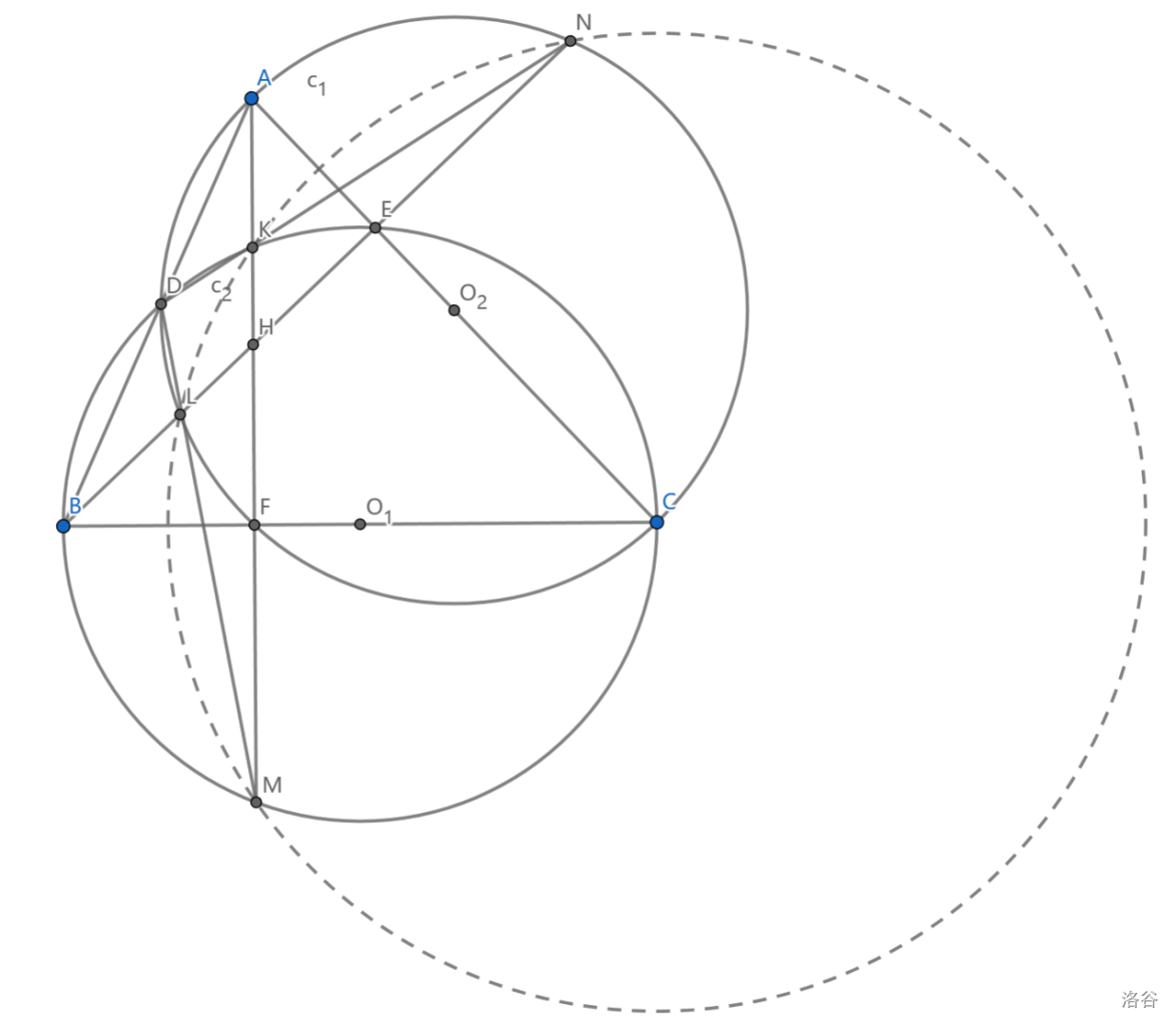
设 \(\triangle ABC\) 中以 \(AC,BC\) 为直径的圆分别为 \(c_1,c_2\) , \(A,B,C\) 对应的垂足为 \(D,E,F\) , \(AF\cap c_2=K,M,BE\cap c_1=L,N\) ,求证: \(AB,ML,NK\) 共点
画个图就可以知道它们的交点就是 \(D\) 。
法一:一个显然的事实是 \(H\) 是在两圆的根轴上的,给出了 \(KLMN\) 共圆,而这个圆的圆心(看上去)恰好是 \(C\) !于是很自然地联想 \(Brocard\) 定理,就能做完这道题。
因为 \(CN=CL,CK=CM\) ,所以 \(C\) 是两条中垂线的交点,它只能是圆心。
我们声称 \(H\) 关于 \(\odot C\) 的极线就是 \(AB\) ,这样根据 \(Brocard\) 定理, \(NK\cap ML\) 就在 \(AB\) 上,就完成了证明。记 \(D\) 是 \(C\) 在 \(AB\) 上的垂足,只要证 \(CH\cdot CD=R^2\)
由 \(ADHE\) 共圆知 \(CH\cdot CD=CE\cdot CA=CE^2+CE\cdot CA\overset{ALCN共圆}{=}CE^2+LE^2=R^2\) ,证毕
法二: \(ACLN\) 是一个对称的四边形,所以它是调和的
注意到 \(-1=F(A,C,L,N)\overset{BE}{=}(B,H;L,N)\) 同理 \((A,H;K,M)=-1\)
显然这两个调和点列关于 \(D\) 透视,问题至此已经结束,具体地可以用同一法来说明:
\(D'=ML\cap NK\) ,则 \(-1=(B,H;L,N)\overset{D'}{=}(A',H;M,K)\) ,则 \(A=A'\) , \(AD'B\) 共线,证毕
例4
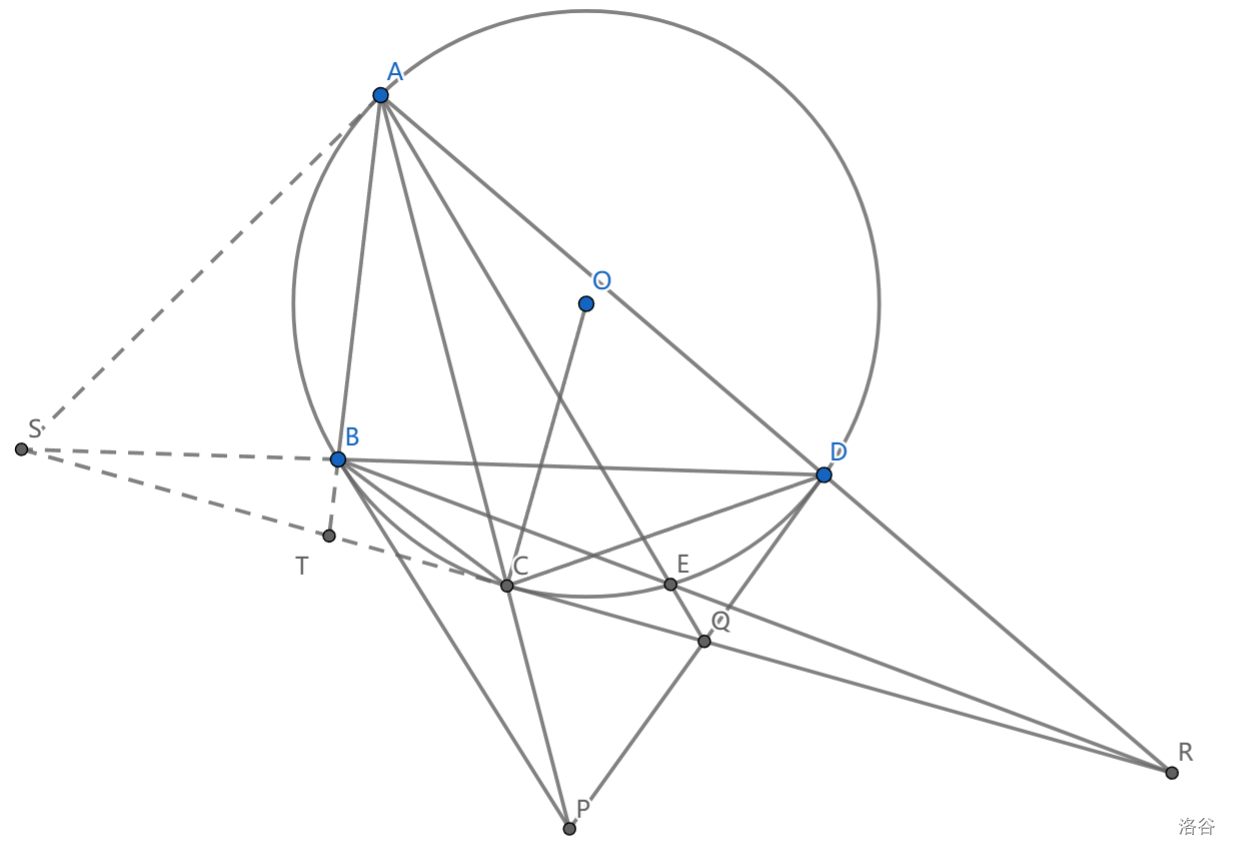
如图,调和四边形 \(ABCD\) 内接于 \(\odot O\) , \(BD\) 的极点为 \(P\) ,过 \(C\) 的切线与 \(DP,DA\) 分别交于 \(Q,R\) , \(AQ\) 与 \(\odot O\) 交于 \(E\) ,证明: \(BER\) 共线
这题可以直接用射影变换。我们来讲一个透视的做法
可以看到 \(ACED\) 是一个调和四边形,如果要证 \(BER\) 共线,换而言之, \(E\) 在 \(CQ\) 上的投影(通过 \(B\) )就是 \(R\) ,可以通过 \(B\) 点透视,具体地说,定义 \(R'=BE\cap CQ\) ,有
\(-1=B(A,E;C,D)\overset{CQ}{=}(T,R';C,S)\)
来看看 \((T,R;C,S)\) 。我们再透视一次,可以看到 \(A\) 是个不错的点,将其透视到圆上。
\((T,R;C,S)=A(B,D;C,S)\)
由于 \(ABCD\) 是调和四边形,现在只要证 \(AS\) 是切线就行了。
注意到 \(S=BD\cap CQ=l_p\cap l_c\) ,所以 \(l_s=CP\) ,而 \(A\in CP\) ,证毕。(用到推论 \(9.2\) 的思想)
这个推论能有效地转换三点共线和三线共点的问题。在处理这些问题之前, \(Pascal\) 定理是极其重要的:
定理 \(11\) :设 \(ABCDEF\) 是圆内接六边形(不一定是凸的),则 \(AB\cap DE,BC\cap EF,CD\cap FA\) 共线。
证明:我们将证明其推广形式:
三条圆锥曲线 \(C_1,C_2,C_3\) 都经过 \(A,B\) 两点, \(C_2\cap C_3=A,B,P_1,P_2,C_3\cap C_1=A,B,Q_1,Q_2,C_1\cap C_2=A,B,R_1,R_2\) 则 \(P_1P_2,Q_1Q_2,R_1R_2\) 共点
取其中两条圆锥曲线退化为两条直线即可
\(Bezout\) 定理:若两条三次曲线有九个交点,另一条三次曲线经过这九个点中的八个,那么它经过第九个点。
这是因为三次曲线有 \(10\) 个系数,需要 \(9\) 个点确定,但如果 \(9\) 个点不能确定一条三次曲线,也就是有两条三次曲线经过它们,那它们构成的方程中就一定出现了线性相关的情况,就可以由其中八个点推出第九个点
构造三次曲线 \(F_1=C_1\cup P_1P_2,F_2=C_2\cup Q_1Q_2,F_3=C_3\cup R_1R_2\) ,设 \(P_1P_2\cap Q_1Q_2=K\)
则 \(F_1,F_2\) 都经过 \(ABP_1P_2Q_1Q_2R_1R_2K\) ,从而 \(F_3\) 经过它,即 \(K\in R_1R_2\) ( \(K\) 不在 \(C_3\) 上)
当然,初等的证明可以在任何一本几何教材上找到。
下面的例子展示了极点极线与 \(Pascal\) 定理的应用
例5
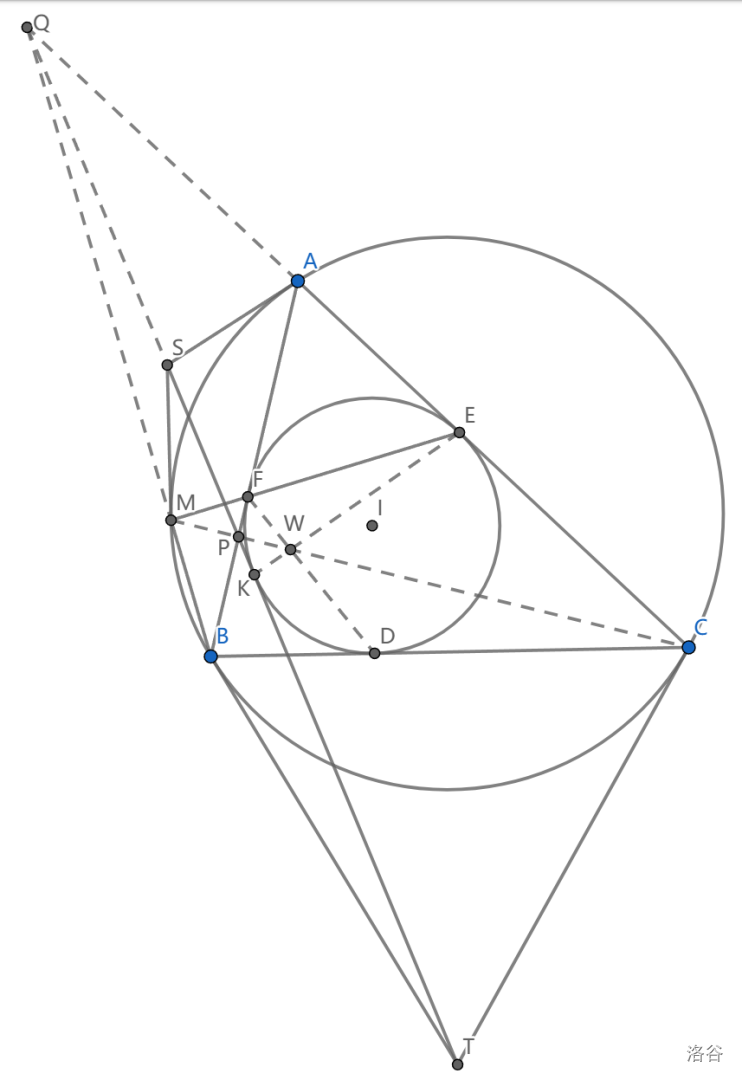
如图, \(\triangle ABC\) 的内切圆 \(\odot I\) 与 \(AB,AC,BC\) 切于 \(F,E,D\) ,射线 \(EF\) 交 \(\odot(ABC)\) 交于 \(M\) , \(S\) 是 \(AM\) 的极点, \(T\) 是 \(BC\) 的极点,求证: \(ST\) 是内切圆切线。
我们令 \(P=AB\cap MC,Q=BM\cap AC\) ,根据推论 \(9.3\) ,我们看到 \(PQST\) 共线,然后用 \(PQ\) 代替 \(ST\)
下面我们关于内切圆做分析。 \(PF,QE\) 已经是切线了,作另一条切线 \(PK\) ,我们要证 \(QK\) 也是切线。
我们需要审视图中的条件。 \(M=PC\cap EF\) ,于是 \(M\) 的极线上有 \(A\) 和 \(l_C\cap l_P=ED\cap FK\)
注意 \(EDFK\) 是内切圆上的点,所以根据 \(Brocard\) 定理,若 \(ED\cap FK\) 在 \(M\) 的极线上,那么 \(M\) 一定在 \(FE\cap KD,FD\cap EK=W\) 的连线上(那是 \(FK\cap ED\) 的极线),所以 \(M=FE\cap KD\)
那么 \(AW\) 是 \(M\) 的极线。现在 \(W=DF\cap l_M\) 给出 \(l_W=BM\) ,从而 \(Q\) 在 \(W\) 极线上,那么 \(l_Q=WK\) 过点 \(K\) ,证毕。
注:我们其实没用到 \(A\) ,在书写答案时可以省略 \(A\) 。但是在做题过程中,用 \(9.2\) 的思想思考是更完整的方式。
例6
(布利安桑定理)若六边形 \(ABCDEF\) 外切于圆,证明: \(AD,BE,CF\) 共点
根据上面的引理,只要证 \(AD,BE,CF\) 对应的极点共线就好。
而 \(AD\) 的极点是 \(l_A,l_D\) 的交点,\(l_A\) 就是 \(AB,AF\) 与圆切点的连线。
于是把六个切点作出,发现该命题即等价于帕斯卡定理。
例7
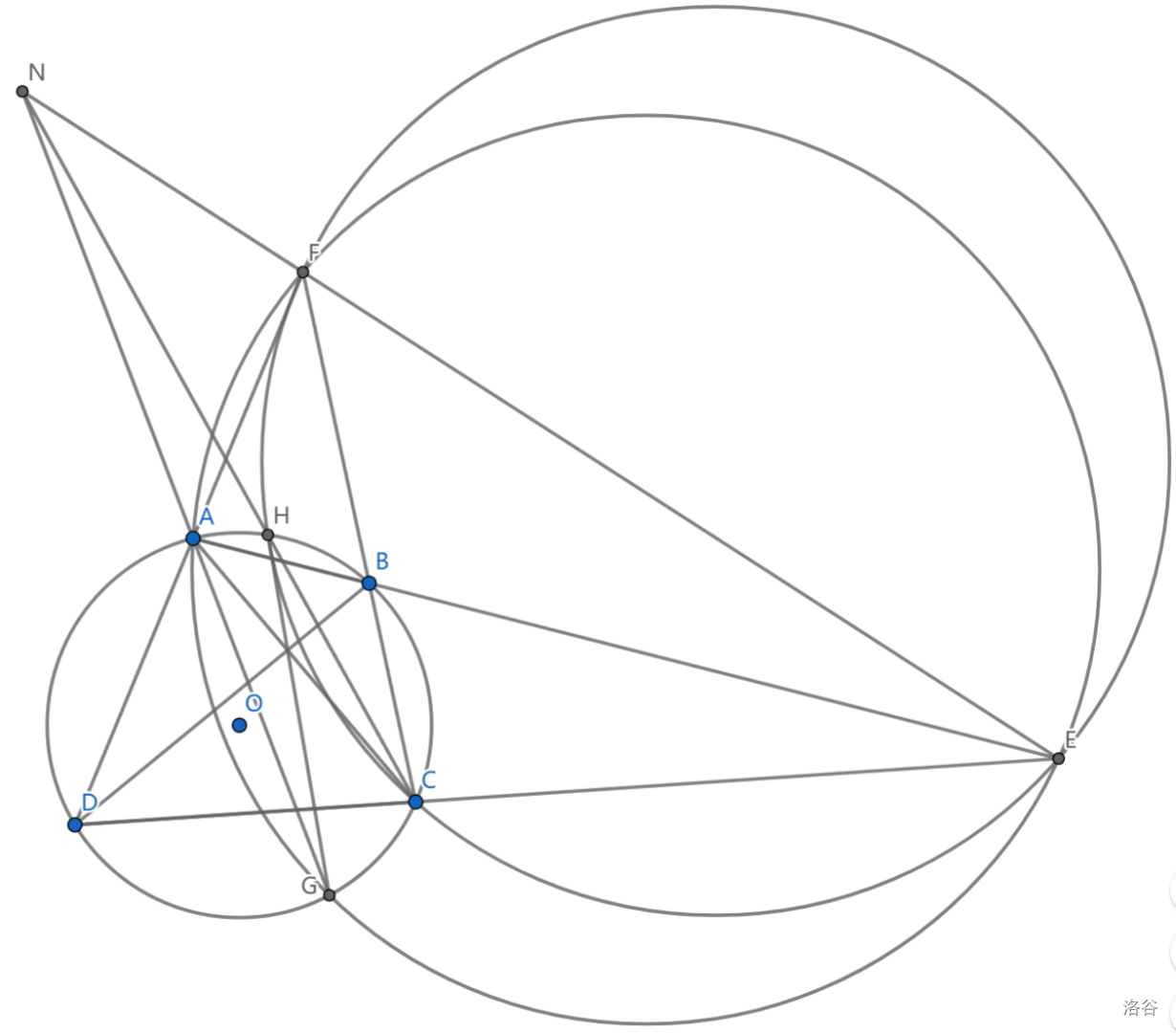
设四边形 \(ABCD\) 内接于圆 \(c\) , \(E=AB\cap CD,F=AD\cap BC\) ,设 \(\odot (AEF),\odot (CEF)\) 分别与 \(c\) 交于 \(G,H\) ,求证: \(GH,AC,BD\) 共点
设 \(R=AC\cap GH\) ,要证 \(R\) 在 \(BD\) 上,根据 \(Brocard\) 定理,只要证 \(l_R=EF\)
一个不错的事实是(由根心定理给出) \(AG,CH,EF\) 共点。那么用 \(Brocard\) 定理,只要证 \(AH\cap GC\in EF\)
来尝试 \(Pascal\) ,我们要对 \(AH\_CG\_\) 或者 \(HA\_GC\_\) 使用(其实一样的,但是写的时候毕竟从左往右写更自然)
注意到 \(HAAGCC\) 是很好的。因为 \(AA\cap CC\) 根据 \(Brocard\) 定理已经在 \(EF\) 上, \(AG\cap GC\) 也已经在 \(EF\) 上,这就证毕。
例8
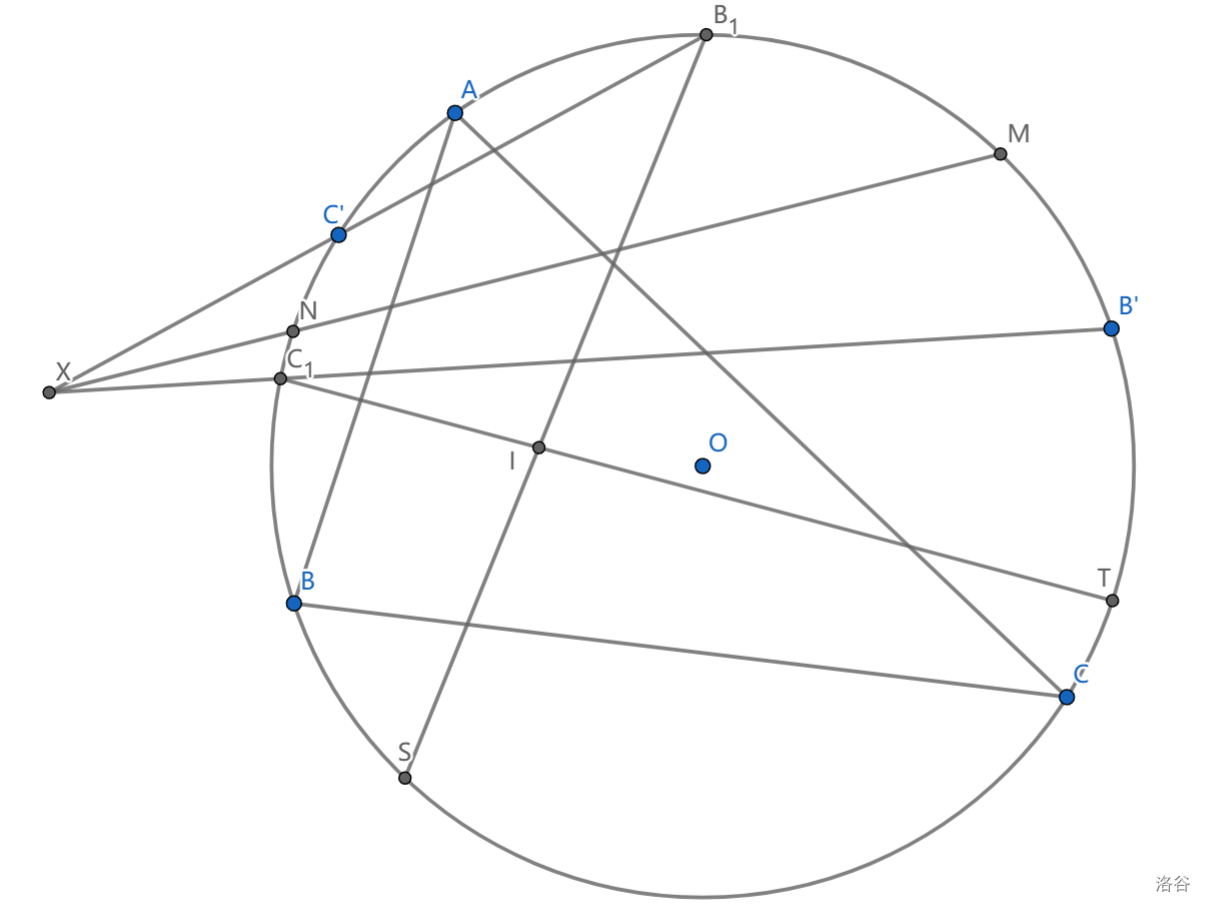
如图, \(\triangle ABC\) 的内心为 \(I\) , \(B-\) 伪内切圆与外接圆切于点 \(B_1\) , \(B'\) 是 \(B\) 的对径点,同理定义 \(C_1,C'\) 。设 \(B'C_1,C'B_1\) 交于 \(X\) ,求证: \(XA=XI\)
取弧 \(AB,AC\) 中点 \(N,M\) ,只要证 \(NMX\) 共线,或者说证明 \(B_1C',B'C_1,MN\) 共点。并且其实 \(OIX\) 也可以看出来是共线的
必须注意的是,应当把 \(X\) 定义为 \(NM\cap B_1C'\) 然后把 \(C_1B'\) 这两个点用六边形交出来,因为 \(B_1,C_1\) 这两个点其实不是很直接的点,但也不能一个都不用
如果这样定义,应当用 \(NM\_B_1C'\_\) 或者 \(NM\_C'B_1\_\) 。我们先很自然地看到了 \(CC'\) 与 \(MS\) 是交于圆心的,这不错,而 \(SB_1\cap CN=I\) ,很好,对 \(NMSB_1C'C\) 有 \(OIX\) 共线。
这里已经做完了。如果我们再定义 \(X'=NM\cap B'C_1\) , \(OIX'\) 同理共线,这就给出 \(X=X'\) ,证毕。
我们以几个阿氏圆的例子结束基础知识的讲解。
例9
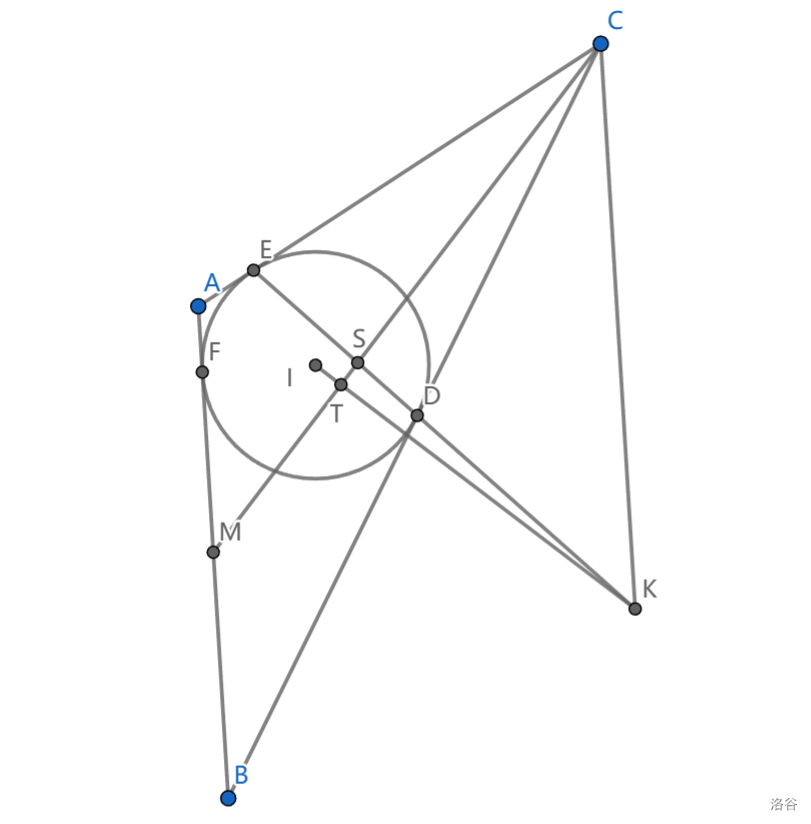
如图, \(\triangle ABC\) 内接圆 \(\odot I\) 切三边于 \(D,E,F\) , \(M\) 是 \(AB\) 中点,过 \(I\) 作 \(CM\) 垂线交 \(DE\) 于点 \(K\) ,求证: \(CK//AB\)
\(ADTIE\) 五点共圆,我们可以记 \(S=DE\cap CM,T=IK\cap CM\)
现在已经有 \(\angle STK=Rt\angle\) ,看看 \(TS\) 是否平分 \(\angle DTE\) 。由共圆, \(\angle DTC=\angle DIC=\angle EIC=\angle ETC\) ,从而 \(-1=(D,E;S,K)\)
透视到直线 \(AB\) 上得到 \(-1=(A,B;M,K')\) , \(K'\) 只能是无穷远点,从而 \(CK//AB\) ,证毕。
例10
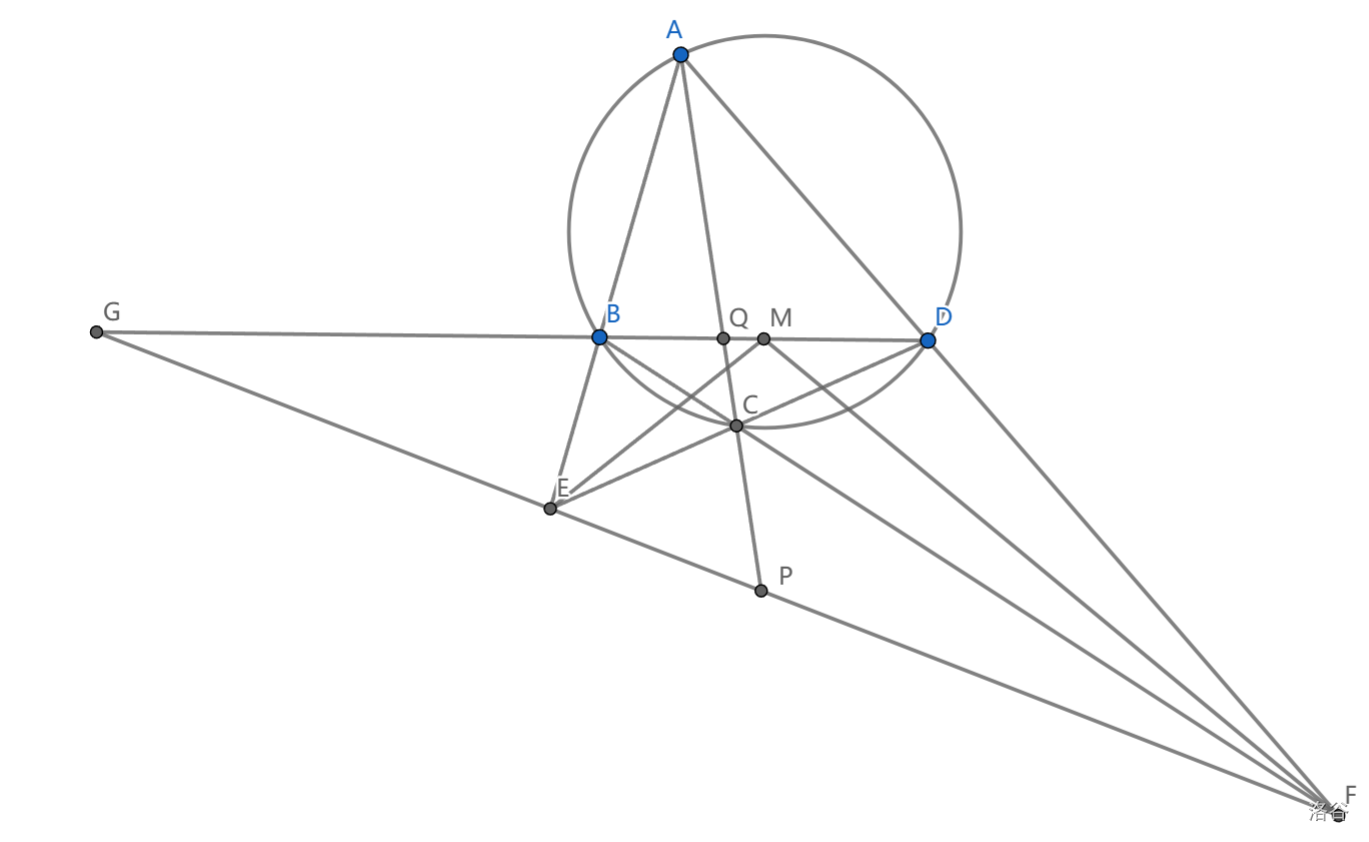
如图,圆内接四边形 \(ABCD\) 中, \(E=AB\cap CD,F=AD\cap BC\) , \(M\) 是 \(BD\) 中点,若 \(\angle BME=\angle DMF\) ,求证: \(ABCD\) 是调和四边形
把这个完全四边形补充完整。构造 \(G=EF\cap BD,P=AC\cap EF,Q=AC\cap BD\)
已经有了外角平分线,看看有没有调和点列或者垂直。前者比较明显, \((E,F;P,G)=-1\) ,从而 \(PM\perp BD\)
因为\(Q\in BD\) ,所以 \(BD\) 极点 \(X\in l_Q\) ,根据 \(Brocard\) 定理, \(l_Q=EF\) ,从而 \(X=P\) ,证毕。
定理 \(12\) :\(A,B\) 是关于 \(\Gamma\) 的反演对应点 \(\iff\) \(\Gamma\) 是关于 \(A,B\) 的阿氏圆 \(\iff\) 点圆 \(A,B\) 与 \(\Gamma\) 共轴
例11
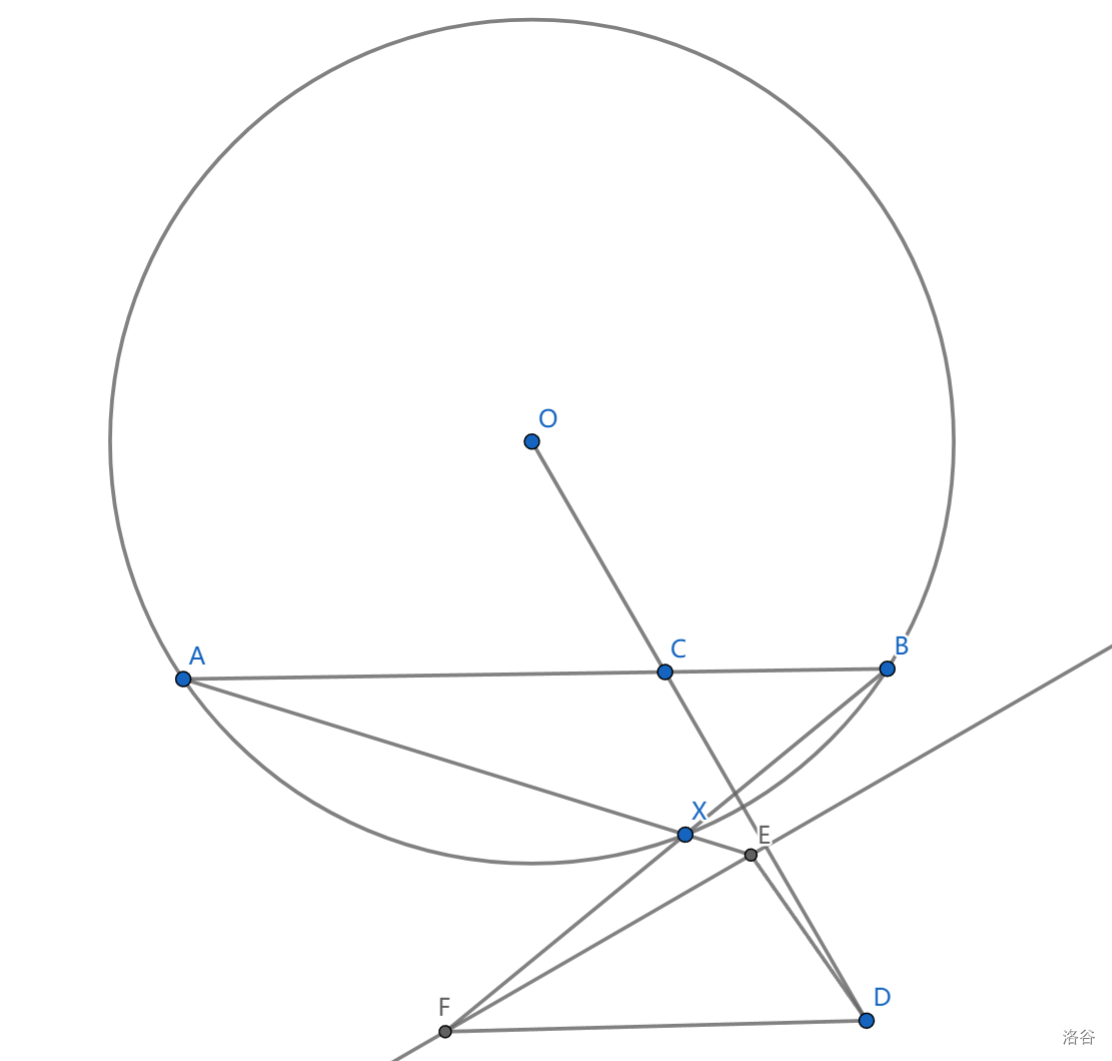
如图, \(AB\) 是 \(\odot O\) 上任一条弦, \(C\in AB\) 且 \(CD\) 关于 \(\odot O\) 为反演对应点。 \(X\) 是弧 \(AB\) 上任一点, \(AX,BX\) 与 \(CD\) 中垂线交于 \(E,F\) ,求证: \(X,E,F,D\) 共圆
根据定理 \(12\) ,点圆 \(C,D\) 和 \(\odot O\) 共轴 \(EF\) ,从而 \(EX\cdot EA=EC^2\) 给出 \(\triangle CEX\sim\triangle AEC\) ,从而 \(\angle ECA=\angle EXC\) ,同理 \(\angle FCB=\angle FXC\)
来看看 \(\angle EXF=2\pi-(\angle FXC+\angle EXC)=\pi-\angle ECF=\pi-\angle EDF\) ,证毕
准确地来说应该用有向角。
标签:AB,angle,定理,cap,四边形,几何,triangle,射影 From: https://www.cnblogs.com/Rocking-Yoshi/p/18356980