快速傅里叶变换
前言
关于此算法,应用广泛。但是在 OI 算法竞赛中,我们只关注它“加速多项式乘法” 这一用途。
本文适用于未接触过此算法的初学者。
对于本文用词不当、概念错误等问题,请发布在讨论区,我看到会及时修改,力争全文的每一句话都可以被引用而无误。
由于本文在书写之初只是想要教学算法,但是某些原因,进行了更改,本文适用于 P1919 的题解。
规范
算法的名称为快速傅里叶变换(Fast Fourier Transform)。在一些文章中,它被翻译为“快速傅立叶变换”。其原因为作者 Fourier 的音译问题。本文章按照“傅里叶” 翻译。所有此名称的衍生名词的翻译也遵守此规定。
用途
快速傅里叶变换可以用来加速多项式乘法,将 \(O(n^2)\) 的暴力算法优化为 \(O(n \log n)\) .
并且,我们可以将形如 \(1234\) 这样的十进制数字看作 \(1x^3+2x^2+3x^1+4x^0\) 这个多项式在 \(x=10\) 情况下的值,这也是高精度的原理。两个数字相乘即是两个多项式相乘,所以快速傅里叶变换还可以加速高精度乘法。
请注意,快速傅里叶变换本身的功能就是将多项式从系数表示转化为点值表示(此句后文会进行详尽解释)。上述的例子都是具体场景。
例如,乘法的本质就是一个数字重复加几次,但是它可以用来计算面积、总数等。请理解这两句中的“用途”与“本质”的区别。
在此解释的原因就是希望你不要被这几个例子限制住了你的想象力,算法本身会有无限的组合与变换,莫要局限于“乘法”二字身上。
FFT 还有更多的用途,如信号处理、图像处理、量子计算等领域均有广泛应用,但是本文并不深入研究。
基础知识
本算法严重依赖数学,大部分为高中数学内容,掺杂初中知识,本文一并讲解。本文未进行解释的,即默认你阅读本文章所要掌握的知识,你可以在其它途径查询。
多项式
既然快速傅里叶变换可以用来加速多项式乘法,我们首先要理解明白什么是多项式。
多项式的定义
多项式的定义即是几个单项式的和。因为次数相同的单项式可以合并同类项,所以多项式的最简形式应是一些次数各不相同的单项式加法形式。
\[\begin{aligned} F(x)&=\sum_{i=0}^na_ix^i\\ &=a_nx^n+a_{n-1}x^{n-1}+...+a_0x^0 \end{aligned} \]此多项式 \(F(x)\) 是多项式的一般形式。多项式的所有单项式中最高次数为 \(n\),定义该多项式的次数为 \(n\) . 该多项式的次数界定义为所有 \(m\) 满足 \(m\gt n\) .
多项式的表示
既然我们是 OIer ,那我们必然会联想到一个问题:如何存储多项式?
观察多项式,发现对于 \(n\) 次多项式,每个多项式所不同的只有每个单项式的系数,所以我们可以开辟一个数组,存储多项式。数组的容量,就是多项式所能存储的多项式的最高次数。
如果我们用这种方法,那么多项式 \(A\) 与 \(B\) 相乘就可以写作下列形式(伪代码):
for i from 0 to n
for j from 0 to n
plus A[i] and B[j] to C[somewhere]
不难发现时间复杂度 \(O(n^2)\),在 \(n\) 较大时时,就会非常慢。
那么能否有其它的方法能存储多项式,并且乘法乘起来还很快呢?
当然会有,不然就不会出现此文章。
但是在介绍这种方法之前,我们需要一条引理:
对于一个 n 次多项式,可以用 n + 1 个点来确定。
思考此引理的含义,我们先从特殊情况出发,如果多项式是 1 次的,那么多项式的图像当然是一条直线。
而两点确定一条直线,我们可以用两个点确定这一条直线。
对于普遍情况,此引理也成立。
有了这个非常棒的性质,我们就可以通过两个数组 \(X\) 和 \(Y\) 存储一个多项式。如果点的 \(x\) 默认确定,那么可以只用一个数组存储。
for i from 0 to n
plus A[i] and B[i] to C[i]
是 \(O(n)\) 的时间复杂度!
实际上,我们高兴得有点早了。如果止步于此的话,本文章仍然不会存在。
我们忽略了一个问题:在转换和计算点值时,选点是 \(O(n)\) 计算是 \(O(n)\) ,最后累计 \(O(n^2)\) .
是的,我们的思路是对的,它确实可以将 \(O(n^2)\) 的计算转化为 \(O(n)\) 的计算。但是题目一般都不会是点值表示法,我们需要转换,而转换才是乘法计算中的大头。
而转换,正是快速傅里叶变换的用武之地,它可以将多项式从系数表示法转化为点值表示法,并且时间复杂度只用 \(O(n \log n)\)。
并且,快速傅里叶逆变换还可以将点值表示法转化为系数表示法,时间复杂度同样只有 \(O(n \log n)\) .
而如何实现这样神奇的转换,我们则需要借助复数。
复数
复数是高中数学的内容,此文简略介绍,只保证能够看懂本算法。
复数的引入
在实数域内,根号下的数字只能是正数,不能是负数。
原因很简单,在实数域内,平方满足如下性质:
\[a^2\ge0 \]不愿根号破坏对称美学数学家们就定义了一个数字 \(i\) 满足 \(i^2=-1\) 称为虚数。
是的,数学家们就是这么无聊。
但是也就是这无心之举,却得以使数学的发展再次前进了一大步 —— 数学家们发现 \(i\) 可以带来许多便利。
形如 \(bi\) 的形式的数字叫做纯虚数。
一切数字都可以写作 \(a+bi\) 的形式,这种形式的数字称作复数。
其中,\(a\) 称为实部,\(b\) 称为虚部。
如此,我们就可以得到目前数学上最大的数域:复数域。
复数也可以作为方程的解,并且延伸出一个重要的定理 —— 代数基本定理:简单概括,\(n\) 次方程有且仅有 \(n\) 个根。
复数的运算
复数运算很简单,基本上就是分配律。
有复数 \(z_1=a_1+b_1i\) 以及 \(z_2=a_2+b_2i\),下文讨论两者的四则运算。
复数加法
\[\begin{aligned} z_1+z_2&=(a_1+b_1i)+(a_2+b_2i)\\ &=a_1+b_1i+a_2+b_2i\\ &=(a_1+a_2)+(b_1+b_2)i \end{aligned} \]复数减法
\[\begin{aligned} z_1-z_2&=(a_1+b_1i)-(a_2+b_2i)\\ &=a_1+b_1i-a_2-b_2i\\ &=(a_1-a_2)+(b_1-b_2)i \end{aligned} \]复数乘法
\[\begin{aligned} z_1\times z_2&=(a_1+b_1i)\times(a_2+b_2i)\\ &=a_1(a_2+b_2i)+b_1i(a_2+b_2i)\\ &=a_1a_2+a_1b_2i+a_2b_1i-b_1b_2\\ &=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i \end{aligned} \]复数除法
\[\begin{aligned} z_1 \div z_2&=\frac{a_1+b_1i}{a_2+b_2i}\\ &=\frac{(a_1+b_1i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)}\\ &=\frac{(a_1a_2+b_1b_2)+(a_2b_1-a_1b_2)i}{a_2^2-b_2^2}\\ &=\frac{a_1a_2+b_1b_2}{a_2^2-b_2^2}+\frac{a_2b_1-a_1b_2}{a_2^2-b_2^2}i \end{aligned} \]复数的几何意义
同实数一样,复数也有几何意义。实数与数轴上的点一一对应,复数则以坐标轴上的点一一对应。
但是,这个坐标轴需要改造一下:
复数的基本形式是 \(a+bi\),我们按照此规定了复数的坐标轴。
横轴叫做实轴,代表复数的实部 \(a\)。纵轴是虚轴,代表复数的虚部 \(b\) .
而此坐标轴形成的平面,叫做复平面。
复数在复平面下的加减乘除也有特殊的意义,但是涉及到向量,超出了本文章的讨论范围,如果你对此有兴趣,请参阅一些书籍或文章。
共轭复数
复数 \(z=a+bi\) 的共轭复数定义为 \(a-bi\) 记作 \(\bar z\) .
欧拉公式
大数学家欧拉在数学界有着不可撼动的地位,其欧拉公式就有好几个(我曾一度疑惑为什么此欧拉公式非彼欧拉公式)。
本文章所讨论的,就是那个数学上最美妙的公式(我认为的)。
这个公式,有自然常数 \(e\) 和圆周率 \(\pi\),有乘法的单位元 \(1\),有加法的单位元 \(0\) .
但其实此式子只是欧拉公式的一个特殊情况,真正的欧拉公式长这样:
\[e^{i\theta}=\cos(\theta)+i\sin(\theta) \]此公式将指数函数延伸到复数域,并与三角函数建立起了桥梁。
单位根
单位根的定义
考虑一个这样的方程:
\[\omega^n=1 \]根据代数基本定理,此方程有 \(n\) 个根。
而这个方程还有特殊的性质,我们可以通过复平面来窥其究竟。
下图是当 \(n=6\) 时的方程 6 个根在复平面上的分布。
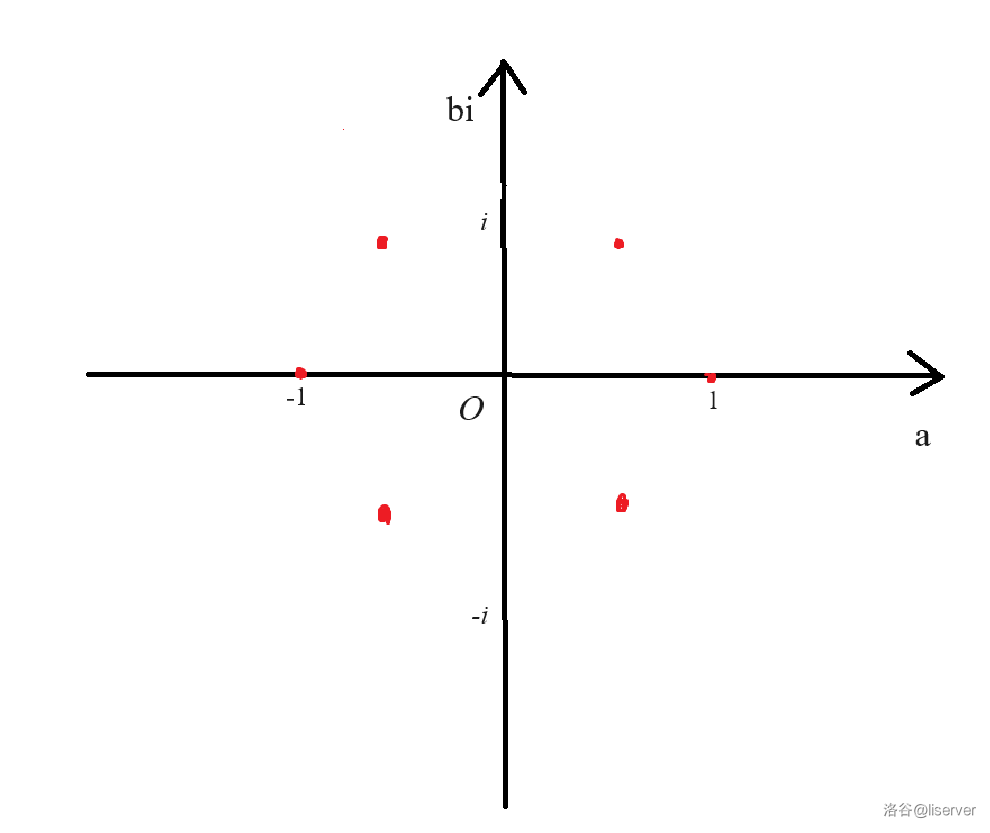
是否发现,这 \(n\) 个解在以原点为圆心,以 1 为半径的一个圆上均匀分布?
这个圆叫做单位圆。
可以证明,\(\omega\) 是单位圆的 \(n\) 等分点。
此方程的 \(n\) 个解,叫做 \(n\) 次单位根,记作 \(w_n\) .
根据欧拉公式,我们还可以直接求出单位根:
\[\begin{aligned} w_n&=e^{\frac{2\pi i}{n}}\\ &=\cos(\frac{2\pi}{n})+i\sin(\frac{2\pi}{n}) \end{aligned} \]单位根的性质
\(n\) 次单位根有 \(n\) 个,都是单位圆的 \(n\) 等分点,此性质已经在上文提到。
\(n\) 个单位根分别是欧拉公式求出的 \(\omega_n\) 的 \(m\) 次方, \(m\) 满足 \(0 \le m \le n\) .
例如, 4 次单位根分别是 \(\omega_4^1, \omega_4^2, \omega_4^3, \omega_4^4\) .
同时, \(\omega_n^0=\omega_n^n=1\) .
现在提出一条引理(消去引理):
\[w_{dn}^{dk}=w_n^k \]关于此引理的证明,可以直接带入公式:
\[w_{dn}^{dk}=e^{\frac{2\pi dki}{dn}}=e^{\frac{2\pi ki}{n}}=\omega_n^k \]根据消去引理,我们可以得到( \(n\) 为偶数):
\[w_n^{\frac{n}{2}}=w_{2}=-1 \]此推论的证明,也很简单:
\[w_n^{\frac{n}{2}}=\omega_{2n}^n=\omega_2=e^{\frac{2\pi i}{2}}=e^{i\pi}=-1 \]根据此结论,还可以得到:
\[w_n^{m+\frac{n}{2}}=\omega_n^m\times w_n^\frac{n}{2}=-\omega_n^m \]第二条引理(折半定理):
如果 \(n\gt0\) 为偶数,那么 \(n\) 个 \(n\) 次单位根的平方集合就是 \(\frac{n}{2}\) 个 \(\frac{n}{2}\) 次单位复数根集合。
证明:
根据消去引理:
\[(w_n^m)^2=w_n^{2m}=w_{\frac{n}{2}}^m \]此时集合的数量仍然是 \(n\) ,而引理说明应该是 \(\frac{n}{2}\) .
\[(\omega_n^{m+\frac{n}{2}})^2=(-\omega_n^m)^2=(\omega_n^m)^2 \]上述式子证明了 \((w_n^{m+\frac{n}{2}})^2\) 与 \((w_n^m)^2\) 相等,也就是集合少了一半。
多项式转换的优化
特殊情况下的优化
如前文所说,将系数表示法转化为点值表示法正是我们迫切需要解决的。
我们只考虑一个简单的多项式:
\[\begin{aligned} F(x)&=4x^2+0x+0x^0\\ &=4x^2 \end{aligned} \]根据前文的讨论,我们需要带入至少三个值。
现在思考一个问题:
我们能否少计算几个点?
换句话说,我们能否在取到一些点后,通过 \(O(1)\) 算出另一些点的值?
答案是存在的,我们只需要把取的点分组,每一组的两个点互为相反数,那么一组中一个点得到了值,另一个点的值也就知道了。
原因就是,这个多项式是一个偶函数,即
\[F(-x)=(-4x)^2=4x=F(x) \]在这个例子中,我们只是简单的优化了选点的方式,就使得计算量减半。
那么,再看一个例子:
\[F(x)=7x^3 \]这个例子是否适用?
当然适用,选点同样是相反数,但是一组中得到的两个值不再相等,而是互为相反数。
原因也很简单, \(F\) 是一个奇函数:
\[F(-x)=(-7x)^3=-(7x)^3=-F(x) \]由特殊到一般
现在,在两个例子中,我们都利用选点的艺术减少了时间复杂度,现在我们将这个艺术从特殊推向一般。
即,对于一个 \(n\) 次多项式,我们考虑其如何优化。
\[F(x) = \sum_{i=0}^{n}a_ix^i \]那么在这个情况下我们不能以普通的奇函数、偶函数来优化,因为这个多项式可能非奇非偶。
那我们只好凑出奇函数和偶函数。
将原多项式拆解为:
\[\begin{aligned} F_1(x)&=a_1x^0+a_3x^1+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}\\ F_2(x)&=a_0x^0+a_2x^1+a_4x^2+...+a_nx^{\frac{n}{2}} \end{aligned} \]我们按照原多项式的系数奇偶拆除了两个新的多项式。
注意,我们默认 \(F\) 的次数 \(n\) 是偶数,如果不是偶数,可以为 \(F\) 添加一个次数为 \(n+1\) 、系数为 0 的单项式,这样 \(F\) 就变成了次数为偶数的多项式。
由于新多项式与原多项式的次数不同,所以不能直接暴力相加。
但是三者肯定有一个微妙的关系,我们进行瞪眼观察,可以得到:
\[F(x)=F_1(x^2)+xF_2(x^2) \]至于为什么不是 \(F_2(x^3)\) ,则是因为我们需要让两个多项式都是偶函数。
这样,我们就将求 \(F\) 的点值变成了求 \(F_1\) 与 \(F_2\) 这两个函数的点值。
而这又变成了两个新的求值问题,并且每个要求点值的多项式次数都是原来的一半。
又因为多项式是偶函数,按照第一个例子,我们要求的值变成了一半的一半。
对于剩下需要求的值,我们仍然可以通过上述策略拆分函数。
如果一切顺利,那么时间复杂度就应该是 \(O(n\log n)\) .
既然我这么说,肯定是不是很顺利的。
注意到 \(x^2 \ge 0\) . 所以,等到 \(F_1\) 和 \(F_2\) 求值时,所有的 \(x\) 都变成了正数,与例子一中互为相反数的要求不符。
快速傅里叶变换
思想
如果你读到现在对于前文复数的知识有些遗忘,请立即返回温习,下文将会高频使用前文的引理、推理。
梳理一下,我们的点子是对的。但是选点上仍然有问题。
我们所需要的,是平方后的数字仍然以相反数成对出现。
既然平方后还能出现负数,则一定需要复数的参与才能完成。
恰好,单位根满足这样的性质。
所以,我们求的 \(n\) 个点,就恰好可以选择 \(n\) 次单位根,正恰好 \(n\) 次单位根有 \(n\) 个。
这正是快速傅里叶变换的精髓所在。
那么我们就将上文中的式子替换为 \(n\) 次单位根。
\[\begin{aligned} F(\omega_n^m)&=F_1((\omega_n^m)^2)+\omega_n^mF_2((\omega_n^m)^2)\\ &=F_1(\omega_n^{2m})+\omega_n^mF_2(\omega_n^{2m})\\ &=F_1(\omega_{\frac{n}{2}}^m)+\omega_n^mF_2(\omega_{\frac{n}{2}}^m) \end{aligned} \]更加惊奇的是,我们将 \(\omega_n^{m+\frac{n}{2}}\) 带入:
\[\begin{aligned} F(\omega_n^{m+\frac{n}{2}})&=F_1((\omega_n^{m+\frac{n}{2}})^2)+w_n^{m+\frac{n}{2}}F_2((\omega_n^{m+\frac{n}{2}})^2)\\ &=F_1((-w_n^m)^2)-\omega_n^mF_2((-\omega_n^m)^2)\\ &=F_1(\omega_n^{2m})-\omega_n^mF_2(\omega_n^{2m})\\ &=F_1(\omega_{\frac{n}{2}}^m)-\omega_n^mF_2(\omega_\frac{n}{2}^m) \end{aligned} \]发现带入 \(\omega_n^m\) 与 \(\omega_n^{m+\frac{n}{2}}\) 后两者只差了一个单项式系数的符号,所以我们在求出左半部分时,可以 \(O(1)\) 求出右半部分。
这再次缩减了求值的次数。
并且,根据折半定理,求 \((\omega_n^m)^2\) 的集合实际上就是求所有 \(\omega_{\frac{n}{2}}^m\) 的集合,所以 \(F_1\) 与 \(F_2\) 这两个子问题就变成了求 \(\frac{n}{2}\) 个点值的问题,与父问题大抵相同,只不过是求值的个数少了一半,满足递归的条件。
这样,我们就可以递归地求解 \(F_1\) 与 \(F_2\) .
不过这次我们没有用上偶函数的思想,而是在拆解的时候做了文章,同样缩小了一半的范围。
不难发现这是分治的思想,时间复杂度 \(O(n\log n)\) .
实现
关于这个算法的实现,一共有两种方法,一种是按照上面所讲述的递归实现,另一种是继续研究,将“拆分”改为“合并”的非递归实现。
递归实现
递归实现没有什么新的理论知识,完全按照上文的实现,请直接阅读伪代码:
func FFT(a)
n = a.length // a 必须是 2 的 n 次幂
if n == 1
return a // 只有一个常量 代入值必定是本身
wn = complex(cos(2 * pi / n), sin(2 * pi / n))
w = complex(1, 0)
a1 = {a[1], a[3], a[5], ..., a[n - 1]} // 根据奇偶性对系数分组
a2 = {a[0], a[2], a[4], ..., a[n]}
y1 = FFT(a1) // 递归地调用、分解
y2 = FFT(y2)
y = {} // 返回值
for m from 0 to n / 2 - 1
y[m] = y1[m] + w * y2[m]
y[m + n / 2] = y1[m + n / 2] - w * y2[m + n / 2]
w = w * wn // 得到下一个单位根
return y
非递归实现
观察系数在每轮递归后的位置所形成的树,注意叶节点的位置以及它的原位置。
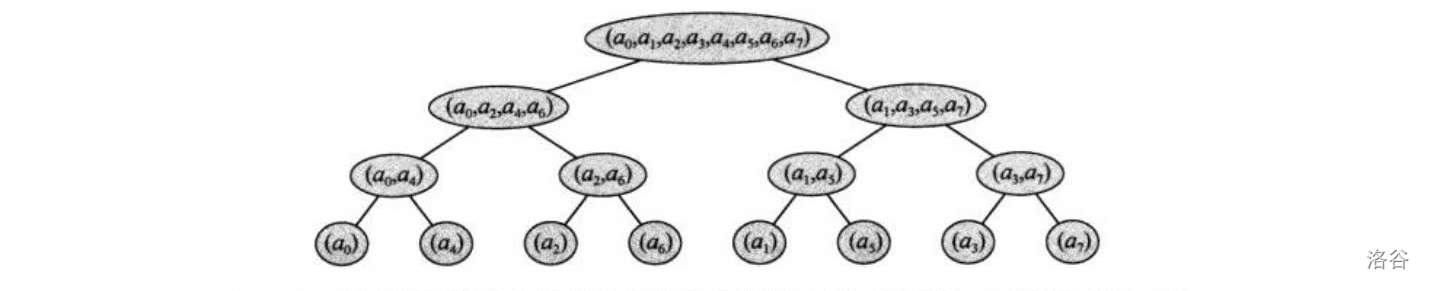
可以证明,对于每一个系数,它最后位置位于自身二进制的“倒数”(从 0 开始计数)。
所谓“倒数”即将原二进制反转,得到新的二进制数字。
例如,处于第 \(6=(110)_2\) 位置的系数最终位于 \(3=(011)_2\) 位置。
那么,我们可以先将所有系数调整到最终的位置,随后合并。
我们按照这棵树来进行遍历,第一层循环遍历树的每一层,第二层循环遍历目前的合并位置,第三层循环则开始进行合并。
需要注意,我们表面上是在遍历一棵树,实际上我们是在遍历一个数组。
伪代码:
func FFT(a)
change_pos(a) // 将每个系数移动到最终位置
n = a.length
for layer from 1 to log2(n) // 遍历树的层数
len = power(2, layer) // 每一组的长度(一组即两个节点)
wn = complex(cos(2 * pi / len), sin(2 * pi / len)) // 计算单位根
for pos from 0 to n - 1 by len // 合并到的位置
w = complex(1, 0)
for i from 0 to len / 2 - 1 // 开始合并
t = w * a[pos + i + len / 2]
u = a[pos + i]
a[pos + i] = u + t
a[pos + i + len / 2] = u - t
w = w * wn
return a
快速傅里叶逆变换
我们将多项式转化为点值表示后,需要再将它转换回来,此时就需要快速傅里叶逆变换。
我们在快速傅里叶变换时,只需要将代入的单位根取倒数,并将得到的结果都除以 \(n\) ,即是快速傅里叶逆变换。
而单位根的倒数,即是单位根的共轭复数。
相应的代码,由于思维难度不大,留作课后练习。
一些例题
P1919 【模板】高精度乘法 | A*B Problem 升级版 - 洛谷
P1919 AC代码
#include <bits/stdc++.h>
const int MAXN = 4000005;
const double PI = 3.1415926535;
// 手写复数实现 防止卡STL
class complex
{
public:
// z = a + bi
double a, b;
complex() = default;
complex(double _a, double _b) : a(_a), b(_b) {}
complex operator+(complex other)
{
return complex(a + other.a, b + other.b);
}
complex operator-(complex other)
{
return complex(a - other.a, b - other.b);
}
complex operator*(complex other)
{
return complex(a * other.a - b * other.b, a * other.b + other.a * b);
}
void operator+=(complex other)
{
*this = *this + other;
}
void operator-=(complex other)
{
*this = *this - other;
}
void operator*=(complex other)
{
*this = *this * other;
}
};
// 修改后系数的位置
int rev[MAXN];
void FastFastTle(complex arr[], int len, int flag)
{
// 将系数移动到最终位置
for (int i = 0; i < len; i++)
{
// 防止系数移动两遍后回去
if (i < rev[i])
{
// 开始交换
std::swap(arr[i], arr[rev[i]]);
}
}
// 层数
for (int h = 2; h <= len; h <<= 1)
{
// 通过欧拉公式计算单位根
complex wn = complex(std::cos(2 * PI / h), std::sin(flag * 2 * PI / h));
// 位置
for (int pos = 0; pos < len; pos += h)
{
// 所带入不同的单位根
complex w = complex(1, 0);
for (int k = pos; k < pos + h / 2; k++)
{
// 开始合并
complex u = arr[k];
complex t = w * arr[k + h / 2];
arr[k] = u + t;
arr[k + h / 2] = u - t;
w *= wn;
}
}
}
// 快速傅里叶逆变换要求在计算后每一项都除以 n
if (flag == -1)
{
for (int i = 0; i < len; i++)
{
arr[i].a /= len;
}
}
}
complex a[MAXN], b[MAXN];
int main()
{
// IO优化
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
std::string stra, strb;
std::cin >> stra >> strb;
const int lena = stra.size(), lenb = strb.size();
for (int i = 0; i < lena; i++)
{
a[i] = complex(stra[lena - 1 - i] - '0', 0);
}
for (int i = 0; i < lenb; i++)
{
b[i] = complex(strb[lenb - 1 - i] - '0', 0);
}
int y = 1;
while (y < 2 * lena || y < 2 * lenb)
{
y <<= 1;
}
for (int i = lena; i <= y; i++)
{
a[i] = complex(0, 0);
}
for (int i = lenb; i <= y; i++)
{
b[i] = complex(0, 0);
}
FastFastTle(a, y, 1);
FastFastTle(b, y, 1);
for (int i = 0; i < y; i++)
{
a[i] *= b[i];
ans[i] = 0;
}
FastFastTle(a, y, -1);
for (int i = 0; i < y; i++)
{
// 此处+0.5然后取整相当于四舍五入
ans[i] += (int)(a[i].a + 0.5);
// 进位
ans[i + 1] += ans[i] / 10;
ans[i] %= 10;
}
int h = lena + lenb + 2;
while (ans[h] == 0 && h >= 0)
{
h--;
}
if (h == -1)
{
std::cout << 0;
}
else for (; h >= 0; h--)
{
std::cout << ans[h];
}
}
参考与致谢
本文章参考了 OI Wiki 、《算法导论》的相关部分,以及洛谷的部分文章。感谢前人所作的贡献,让我学会了这个算法并得以写出此文章。
标签:frac,变换,傅里叶,omega,complex,复数,多项式,aligned,快速 From: https://www.cnblogs.com/liserver/p/18352540