定义:
-
\(e(x,y)\) 表示 \(\sum_{P(x \rightarrow y)} \omega(P)\)。
-
\(\omega(P)\) 表示 \(P\) 这条路径中所有边权之积。
-
路径组 \((S,p)\) 表示 \(a_{i} \to b_{p_{i}}\) 的一种路径组,即 \(S_{1},S_{2},\dots,S_{n}\)。
-
\((S,p)^{*}\) 表示满足不存在 \(S_{i}\) 与 \(S_{j} \ (i \ne j)\) 有公共顶点的路径组。
-
\((S,p)^{'}\) 表示满足存在 \(S_{i}\) 与 \(S_{j} \ (i \ne j)\) 有公共顶点的路径组。
内容:
构造这样的一个矩阵 \(M\)。
\[M=\begin{bmatrix} e(a_1,b_1)&e(a_1,b_2)&\cdots&e(a_1,b_n)\\ e(a_2,b_1)&e(a_2,b_2)&\cdots&e(a_2,b_n)\\ \vdots&\vdots&\ddots&\vdots\\ e(a_n,b_1)&e(a_n,b_2)&\cdots&e(a_n,b_n) \end{bmatrix}\\ \]而 \(LGV\) 引理告诉我们 \(\det(M)=\sum_{p}(-1)^{\tau(p)}\prod_{i=1}^n e(a_i,b_{p_i})=\sum_{(S,p)^*}(-1)^{\tau(p)}\prod_{i=1}^n \omega(S_i) \\\)。
证明:
首先 \(\sum_{p}(-1)^{\tau(p)}\prod_{i=1}^n e(a_i,b_{p_i})\) 将乘法展开变成 \(\sum_{(S,p)}(-1)^{\tau(p)}\prod_{i=1}^n \omega(S_i)\)。
此时只需要证明 \(\sum_{(S,p)^{'}}(-1)^{\tau(p)}\prod_{i=1}^n \omega(S_i)=0\) 即可。设 \(A\) 为 \((S,p)^{'}\) 为路径组的集合。我们需要构造一个双射 \(A \rightarrow A\) 即 \(f((S1,p1)^{'}) = (S2,p2)^{'}\) 满足:
- \(\tau(p1)+\tau(p2)=0\)
- \(\prod_{i=1}^n \omega(S1_{i})=\prod_{i=1}^n \omega(S2_{i})\)
构造方法如下:选择最小的 \(i\) 满足存在 \(S_{j}\) 与 \(S_{i}\) 有交点,再选择一个最小的 \(j\) 满足 \(S_{j}\) 与 \(S_{i}\) 有交点,且这个交点 \(r\) 离 \(a_{i}\) 最近。
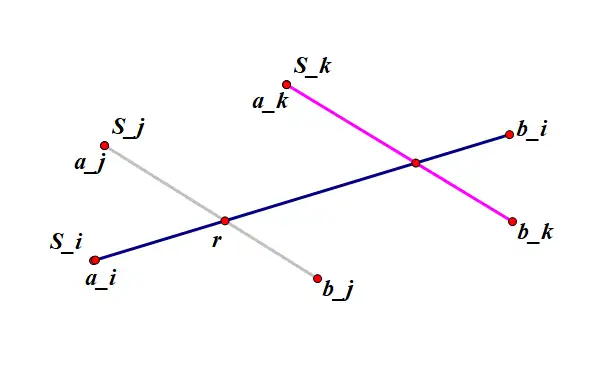
然后交换 \(S_{i}\) 与 \(S_{j}\) 的终点 \(b_{i},b_{j}\),不难发现这样做后满足以上条件。
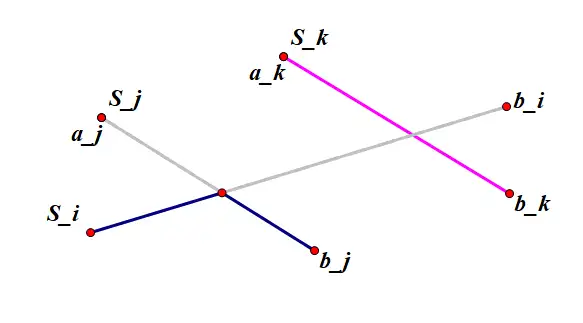
不难发现,此时仍然满足 \(f((S2,p2)^{'})=(S1,p1)^{'}\)。
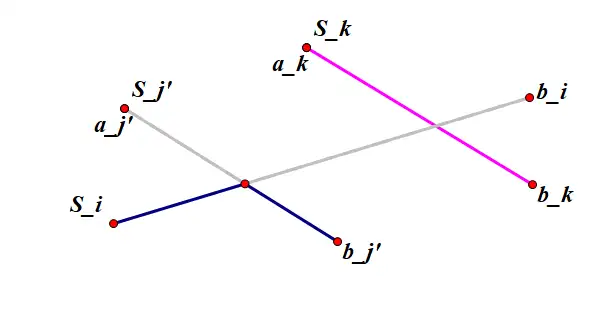
这样就构造出了一个特殊的双射。
应用:
一、P6657 【模板】LGV 引理
将边权全设为 \(1\),由于 \(p\) 一定等于 \(1,2,\dots,n\),那么 \(\sum_{(S,p)^*}(-1)^{\tau(p)}\prod_{i=1}^n \omega(S_i)\) 恰好为路径数。直接求行列式即可。
二、P7736 [NOI2021] 路径交点
对于整个路径方案,它的交点数为两两不同路径间交点数之和
考虑判断两条路径 \(x,y\) 的交点数的奇偶性,记 \(to_{i}\) 表示以 \(i\) 开头的路径的终点。那么路径 \(x,y\) 的交点数为奇数当且仅当 \(to_{x} > to_{y}\)。归纳一下对于整个路径方案它的交点数的奇偶性恰好为 \(to\) 的逆序对的奇偶性。
将边权全设为 \(1\),\(\sum_{(S,p)^*}(-1)^{\tau(p)}\prod_{i=1}^n \omega(S_i)\) 恰好为偶数个交点的路径方案数比有奇数个交点的路径方案数多的个数。\(dp\) 后求行列式即可。
三、[ABC216H] Random Robots
统计方案数除以 \(2^{kn}\) 即为概率。
要求互相不碰撞,可以使用 LGV 引理,但终点没有确定,因此需要枚举最后 \(k\) 个机器人的位置 \(y_{1}<y_{2}<\dots<y_{k}\),记 \(X_{i,j}=\binom{n}{y_{j}-x_{i}}\)。那么答案便是 \(\sum_{y} det(X)\)。考虑用行列式的定义去计算,先枚举 \(P\)(一个排列),那么它的贡献便是
\[(-1)^{τ(P)} \sum_{y} \prod_{j=1}^k\binom{n}{y_{p_{j}}-x_{j}} \]仍然不好计算,由于矩阵的转置的行列式不变,因此贡献也等于
\[(-1)^{τ(P)} \sum_{y} \prod_{j=1}^k\binom{n}{y_{j}-x_{p_{j}}} \]此时可以 dp,记 \(f_{i,j}\) 表示确定了 \(y_{1},y_{2},\dots,y_{i}\) 且 \(y_{i}=j\),使用前缀和优化,总时间复杂度为 \(O(k!nk)\)。无法通过。
用一个二进制数 \(S\) 记录确定 \(P\) 的过程,具体地,记一个 \(f_{S,j}\) 表示当前排列 \(P\) 用过的数为 \(S\),\(y_{i}=j\) 的方案数。需要枚举 \(P_{i}\) 的值,同样也要用前缀和优化,别忘了算上逆序对奇偶性的贡献。时间复杂度 \(O(2^{k}nk)\)。
标签:tau,prod,omega,sum,路径,交点,引理,LGV From: https://www.cnblogs.com/xcs123/p/18310848