简单介绍和资源列表
https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
线代
- vector -- 向量
- 表示 $\vec{a}$ and $\mathbf{a}$ and $\vec{AB} = B - A$
- 指代方向 没有起始点
- 向量的长度$\left | \vec{a} \right |$
- 单位向量 $\hat{a} = \vec{a} / \left | \vec{a} \right |$
- 向量相加
- 向量的表示 -- 默认使用列向量 行向量 $A^T$
向量的乘法
点乘 dot product
$$
\vec{a} \cdot \vec{b} = \left | \vec{a}\right | \left | \vec{b}\right | \cos{\theta}
$$
可以很简单那的得到夹角。
常用于 :
- 去夹角
- 找到投影
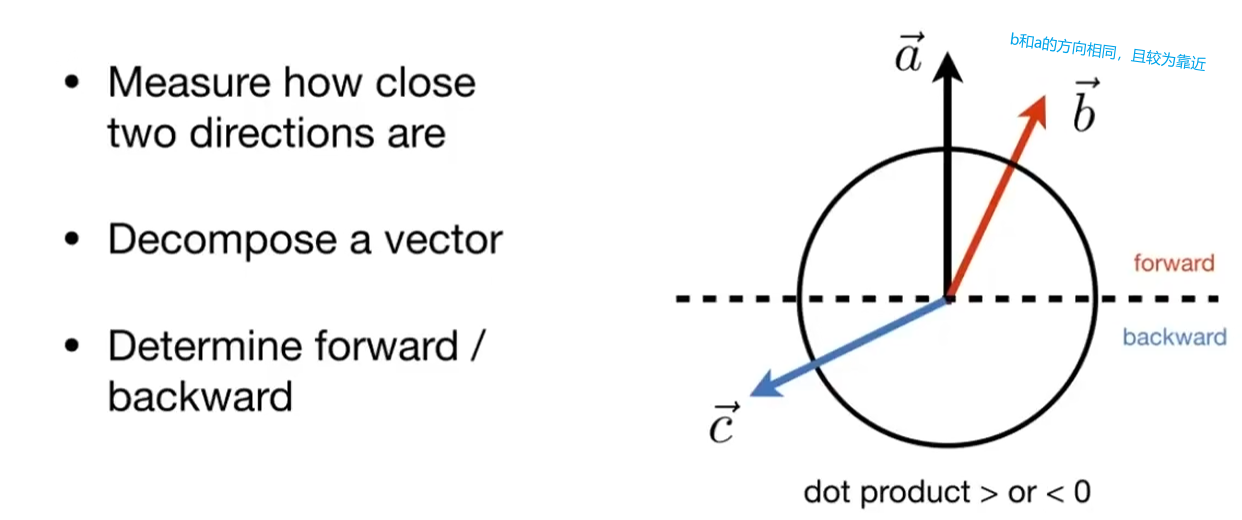
- 确定前后
投影
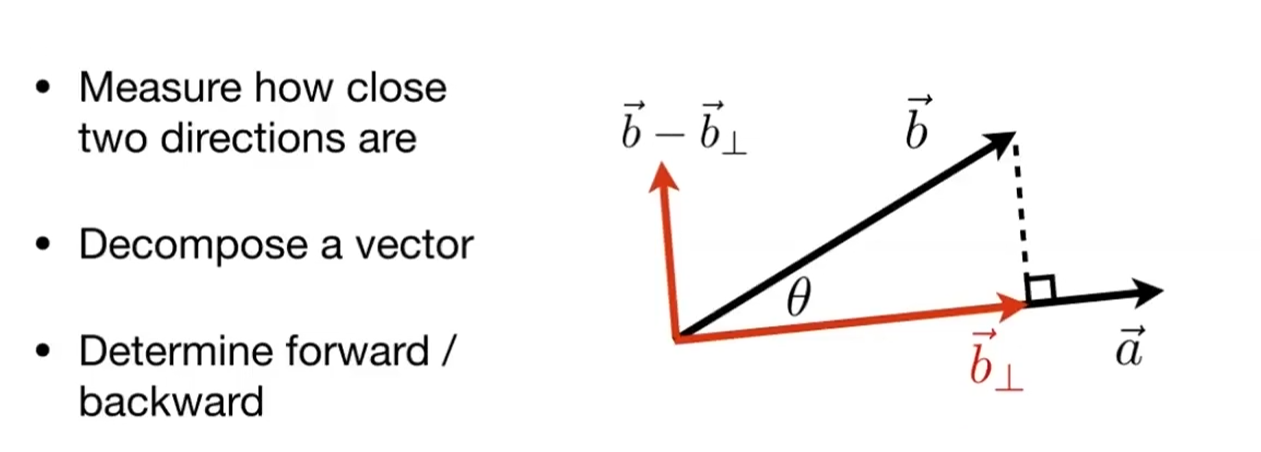
确定方向的前后关系
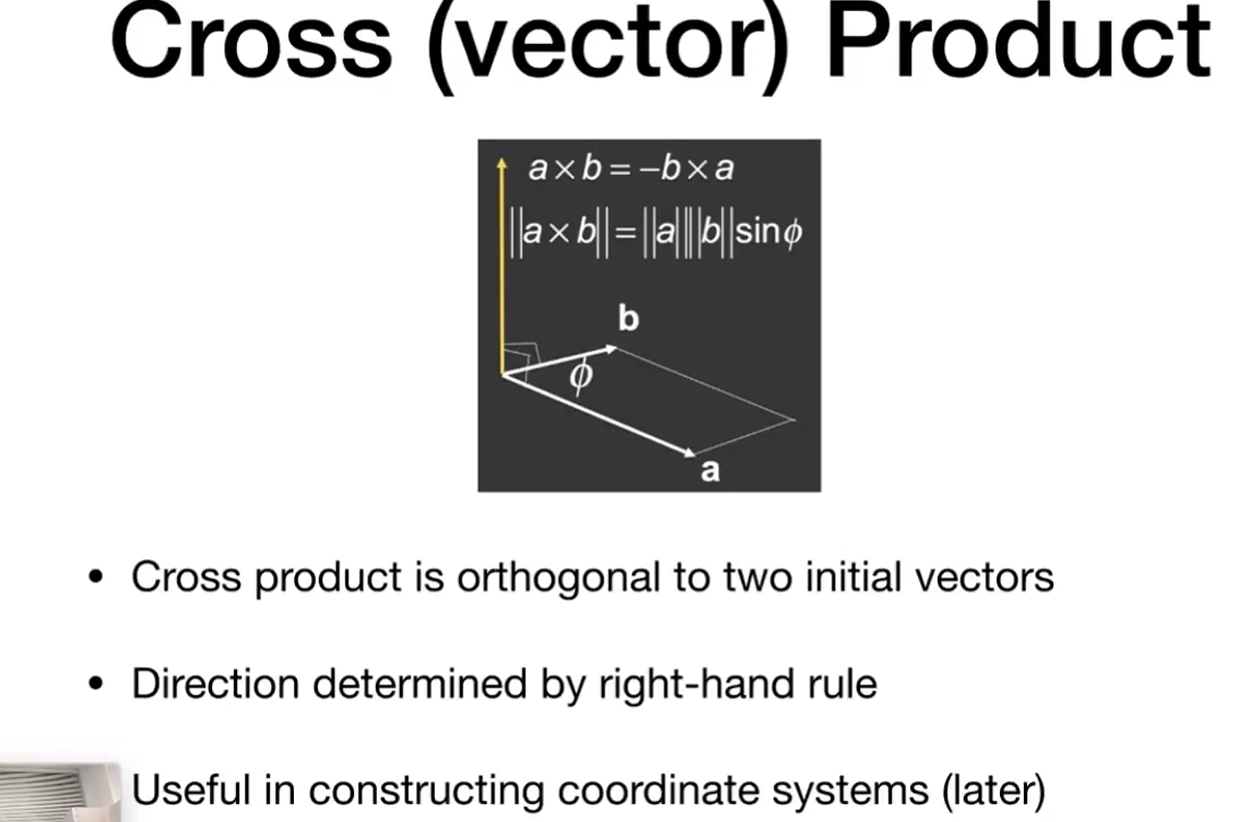
叉乘 cross product --- 这里使用右手坐标系
$$
\vec{a} \times \vec{a} = 0
$$


作用:
- 得到左右的关系 为正 -- 在左 为负 -- 在右
- 判断内外
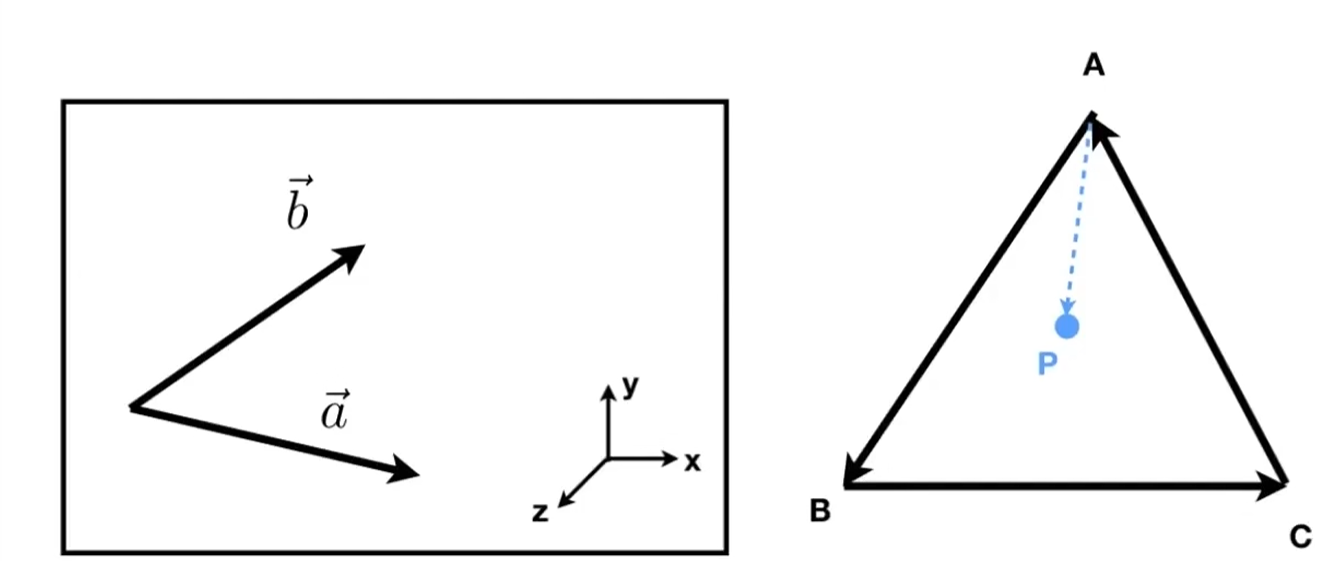
坐标系变换

矩阵
矩阵相乘
转置 $(AB)^T = BTAT$
单位矩阵
$A{-1}A=\mathcal{A}=I$
$(AB)^{-1} = B{-1}A$
