我也不知道为什么要学这玩意
置换:令 \(X\) 是一个非空有限集合,把 \(X\) 到自身的一一映射成为一个“置换”。
记为 \(\delta=\begin{bmatrix}a_1,a_2,\dots,a_n\\b_1,b_2,\dots,b_n\end{bmatrix}\),其中 \(b\) 是 \(a\) 的一组排列。
置换的集合:对于 \(n\) 个元素的集合 \(X\),其置换有 \(n!\) 个,所有置换构成的集合记为 \(S_n\)
置换的简记方式:把循环节放在一起:
例,\(f=\begin{bmatrix}1,2,3,4,5,6\\2,3,1,6,4,5\end{bmatrix}=[1,2,3][4,6,5](1\to2\to3\to1,4\to6\to5\to4)\)
置换的合成运算(composition)
设有两个置换 \(f,g\),则 \(g\circ f(k)=g(f(k))\),\(g=\begin{bmatrix}1,2,\dots,n\\j_1,j_2,\dots,j_n\end{bmatrix}\),\(f=\begin{bmatrix}1,2,\dots,n\\i_1,i_2,\dots,i_n\end{bmatrix}\)
则 \(g\circ f=j_{i_k}\)
性质:
- 置换的合成运算没有交换律
- 有结合律
恒等置换(单位元):
设 \(\tau=\begin{bmatrix}1,2,\dots,n\\1,2,\dots,n\end{bmatrix}\)
对于置换 \(f\),存在置换 \(g\) 是的 \(f\circ g=\tau\),称 \(g\) 是 \(f\) 的逆元,记为 \(f^{-1}\)
置换群:
对于 \(n\) 个元素的置换集合 \(S_n\),有自己 \(G\in S_n\),且满足:
- 合成运算的封闭性。\(G\) 中的任意两个置换 \(f\) 和 \(g\) 的合成运算的结果也在 \(G\) 中。
- 单位元在 \(G\) 中。
- \(G\) 中任意置换 \(f\) 的逆元也在 \(G\) 中。
比如说,一个正方形(4个顶点可以染色)2个颜色进行染色,可以旋转的方案数。
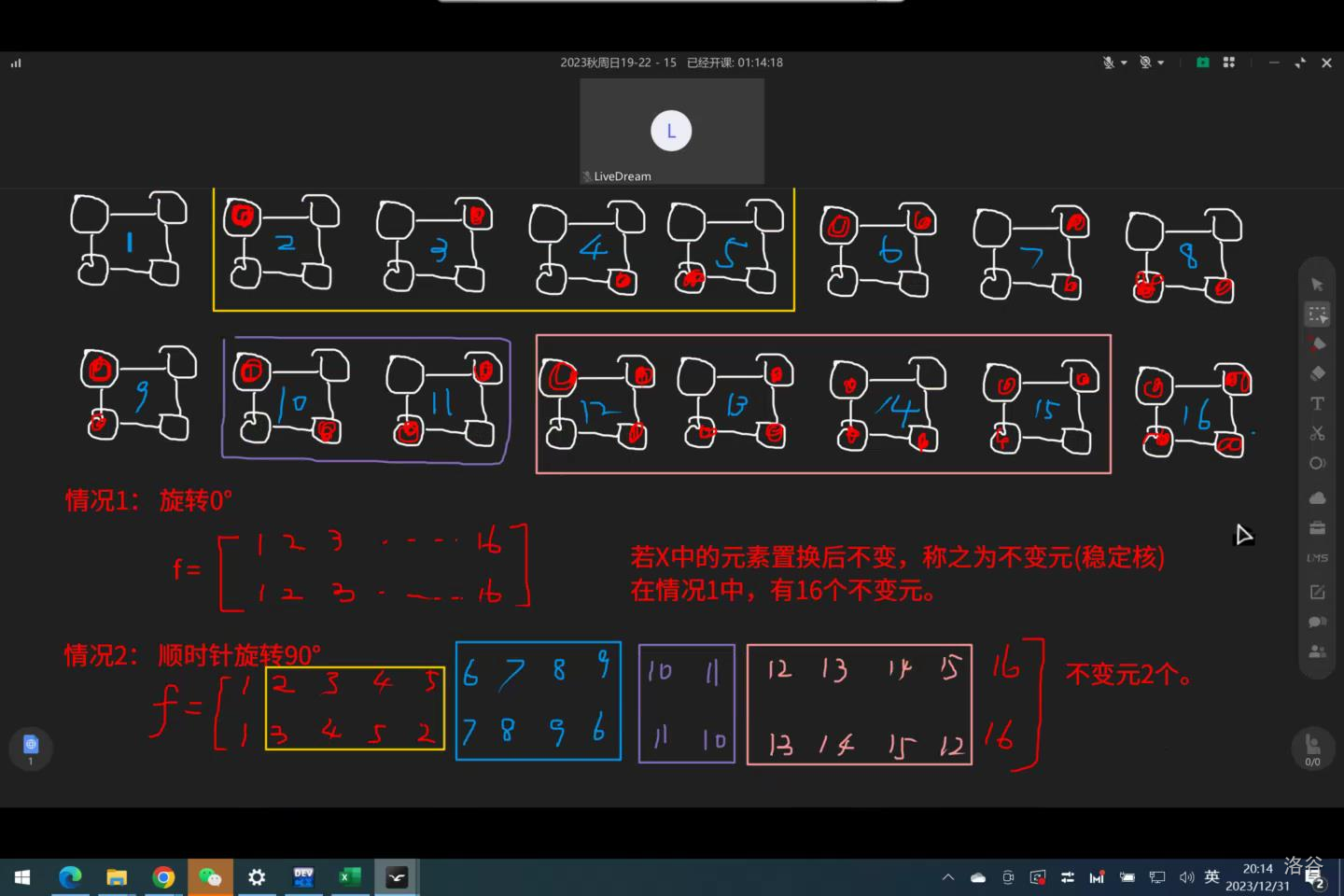
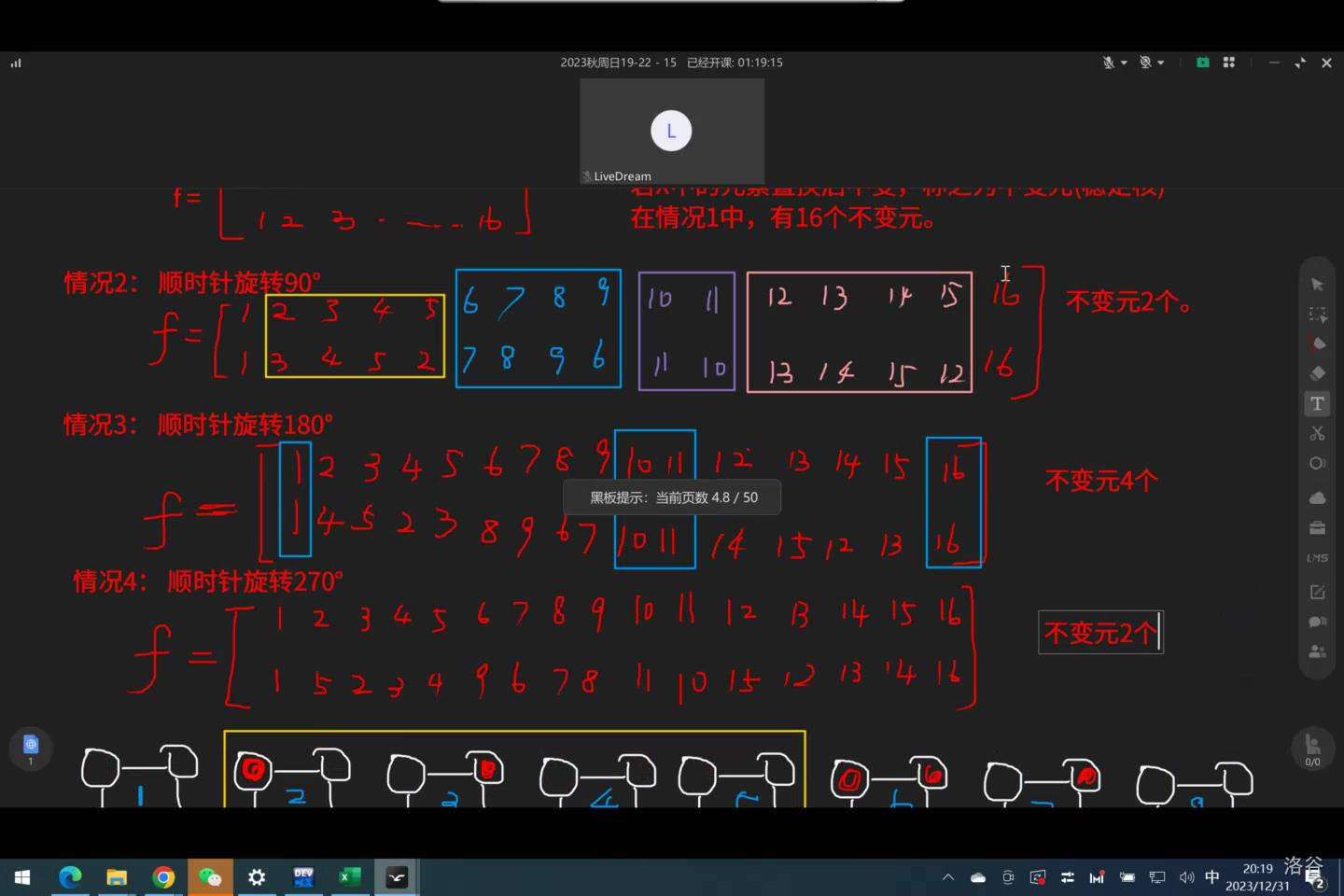
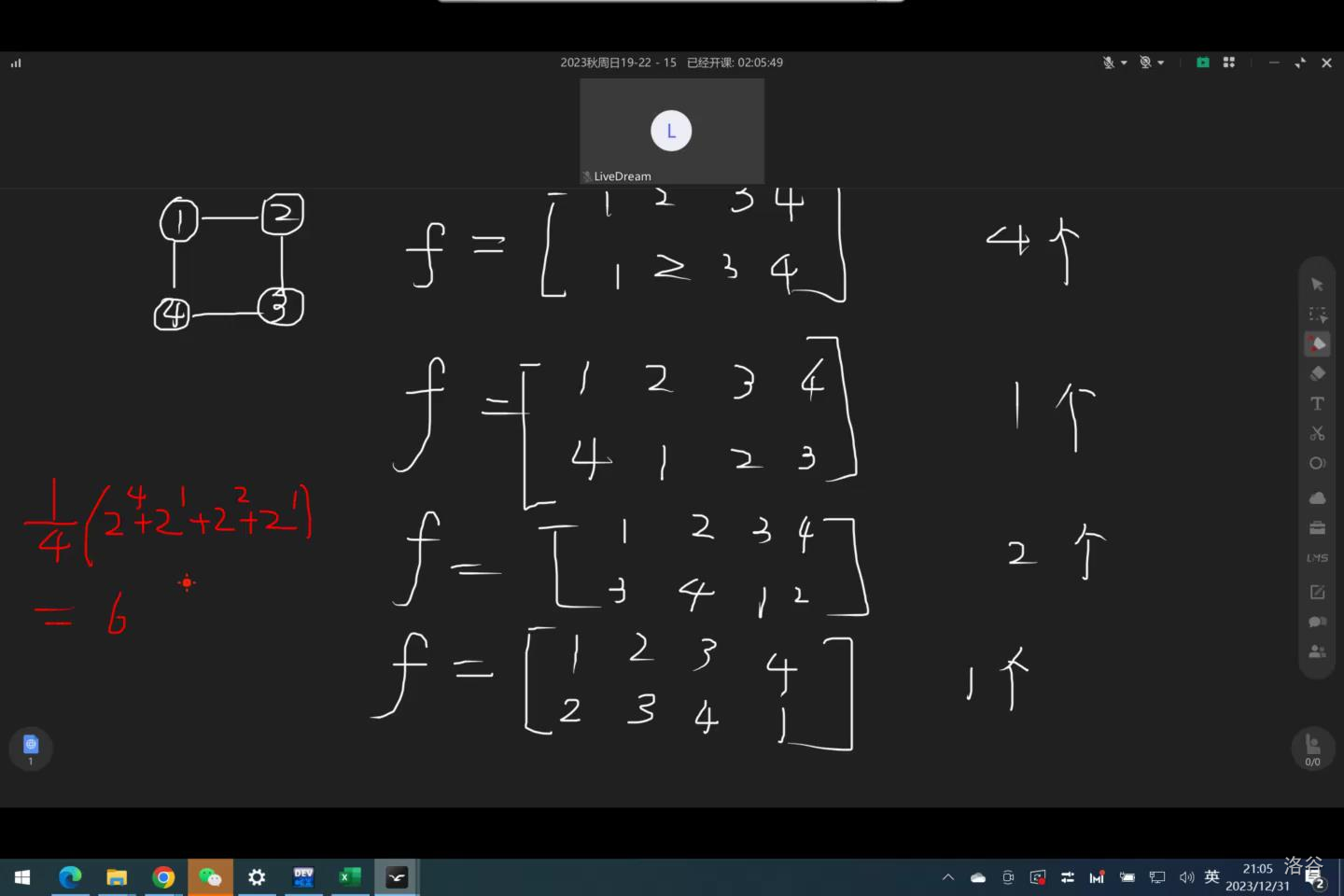
Burnside 如何计数:总染色方案=不变元的和除以旋转的种类数=(16+2+4+2)/4=6
对于置换群 \(G\),定义 \(cnt_f\) 表示置换 \(f\) 中不变元的个数,那么 \(G\) 中的不等价种类(染色方案)(比如,转0度和360度等价)为 \(\frac{1}{|G|}\sum_{f\in G}cnt_f\)
例题1:1...n放置在环中,允许旋转的方案数:
- n种旋转
- 不旋转时,不变元数量是 n!,其余都是0,所以答案是 n!/n=(n-1)!
例题2:例1加上反转,n>=3,等价于2n中变换,所以除以2
Polya计数定理:
设有置换群 \(G={f_1,f_2,...,f_n}\),用 \(m\) 种颜色对 \(n\) 个点染色,则不等价种类数为:
\(\frac{1}{G}\sum_{f\in G}m^{cnt_f}\),其中 \(cnt_f\) 表示 \(f\) 的循环节个数。
仍然以上面的正方形题为例: