标签：frac 入门 置换 times circ 群论 binom 旋转

前言

在 OI 中只会用到群论的一个定理和一个引理来进行本质不同计数：Burnside 引理与 Polya 定理，其它的只是为了让你更好的去理解这两大模块。

这部分其实我也是一知半解，所以有些证明我就不写了。

群

定义

给定集合 \(G\) 和作用于集合 \(G\) 的二元运算 \(\times\)（注意，此 \(\times\) 并非乘法，而是任意一个二元运算，也就是 \(a \times b \rightarrow c\) 的一个运算）

若其满足以下 \(4\) 个性质，则称其为一个群，记为 \((G,\times)\)。

1. 封闭性

   对于任意的 \(a,b\in G\)，满足 \(a\times b \in G\)

2. 结合律
   对于任意的 \(a,b,c\in G\)，满足 \(a\times (b\times c) = (a\times b) \times c\) 成立。

3. 单位元

   若 \(G\) 中存在一个元素 \(e\)，使得对于 \(G\) 中任意的元素 \(a\)，都有 \(a\times e = e \times a = a\)，则称 \(e\) 为单位元。

   可以证明，一个群中的单位元是唯一的。

4. 逆元

   对于 \(G\) 中任意元素 \(a\)，总存在一个 \(b\in G\)，满足 \(a\times b = b\times a = e\)，则称元素 \(b\) 为元素 \(a\) 的逆元，记作 \(a^{-1}\)。

一些性质/定义

阶

若群 \(G\) 里的元素个数有限，则用 \(|G|\) 表示群中元素的个数，称之为群 \(G\) 的阶。

子群

若 \(G\) 和 \(T\) 是两个群，它们的运算相同，且 \(T\) 的集合被 \(G\) 的集合包含，则称 \(T\) 是 \(G\) 的子群，记作 \(T\leq G\)。

下文沿用 \(T\) 是 \(G\) 的子群。

陪集

陪集有左陪集和右陪集两类，这里以左陪集为例。

对于任意的 \(g\in G\)，记 \(gT\) 为 \(G\) 的一个左陪集，表示 \(\forall h\in T\)，变为 \(g\times h\)。同理，\(Tg\) 为 \(G\) 的一个右陪集。

性质

1. \[ \forall g\in G,|T|=|gT| \]

注意到群的性质：逆元唯一，所以对于任意的 \(g \times h_1\) 和 \(g \times h_2\) 其必然不同。

2. \[ \forall g\in G,g\in gT \]

因为 \(T\) 是一个群，所以 \(T\) 肯定包含了单位元 \(e\)，因此 \(e\times g \in gT,g\in gT\)。

3. \[ gT = T \Longleftrightarrow g \in T \]

   封闭性。

4. \[ aT \cap bT \not= \varnothing \Rightarrow aT= bT \]

这意味着一个子群 \(T\) 的陪集的交集要么为空要么这两个陪集相等。

若 \(T \leq G\)，则 \(G/T\) 代表 \(G\) 中所有的 \(T\) 的左陪集即 \(\{gT,g\in G\}\)。

若 \(T \leq G\)，则 \([G:T]\) 表示 \(G\) 中 \(H\) 的不同陪集的数量。

这就得到拉格朗日定理。

拉格朗日定理

对于有限群 \(G\) 与有限群 \(T\)，若 \(T\leq G\)，那么有

\[ |T| \ \text{整除} \ |G| \]

更具体一点，就是

\[|T| \times [G:T] = |G| \]

通过陪集的性质证明，比较自然。

置换

定义

置换，就是一个 \(1\sim n\) 的排列，是一个 \(1\sim n\) 的排列对另一个 \(1\sim n\) 的排列的映射。意思就是我们得到一个排列 \(1,2,\dots,n\)，可以通过置换得到它的映射 \(a_1,a_2,\dots,a_n\)，并且它们一一对应，是一个双射。

\[\binom{1 \ 2\ 3 \dots n}{a_1 \ a_2 \ a_3 \dots a_n} \]

你可以看成是一个函数 \(f(1)=a_1\dots\)，以此类推。

很显然，不同的置换一共有 \(n!\) 种。

置换乘法

其实就是一一对应的起来就好，因为置换就表示的是元素位置的变换。

给个例子：

\[\binom{1 \ 2 \ 3 \ 4}{3\ 2\ 4\ 1}\binom{1 \ 2 \ 3 \ 4}{4 \ 3 \ 1 \ 2}=\binom{1\ 2 \ 3 \ 4}{1 \ 3 \ 2 \ 4} \]

大体就是第一个中 \(1\) 对应 \(3\)，到了第二个中 \(3\) 对应 \(1\)，所以最终就是 \(1\) 对应 \(1\)。以此类推。

可以发现，置换乘法并不支持交换律。

置换的循环与对换

循环时表示置换的一种方法，反映置换的结构，且便于运算。因此我们把 \(m\) 阶循环记为

\[\binom{a_1\ a_2 \dots a_{m-1} \ a_m}{a_2 \ a_3 \dots a_m \ a_1} \]

特别的，当 \(m=2\) 时，二阶循环 \((i,j)\) 叫做 \(i\) 和 \(j\) 的对换。

举个例子来说

\[\binom{1 \ 2 \ 3 \ 4}{4 \ 1 \ 3 \ 2} \]

这里面就有两个循环，一个是 \((1,4,2)\)，另一个就是 \((3)\)，因为你可以看到，\(1\) 对应 \(4\)，\(4\) 对应 \(2\)，\(2\) 又对应 \(1\)，如此循环，\(3\) 自己也是同理的。

由此我们也能得到一个定理：任何一个置换都可以表示成若干个互不相交的循环的乘积，且表示法是唯一的。

置换群

我们令集合 \(N=\{1,2,\dots,n\}\)，令集合 \(M\) 为 \(N\) 的若干个排列后成的集合，再令一个二元组 \(G=(M,\times)\)，这个运算就是置换乘法。若这个二元组满足群的性质，我们称 \(G\) 是一个置换群。

有一个性质：\(N\) 的所有可能的排列与运算置换乘法构成的二元组是一个合法的置换群。证明看看它满不满足群的定义即可。

1. 封闭性：显然，因为所有可能的排列都在里头；

2. 单位元：\(e=(1,2,\dots ,n)\)

   你会发现任意一个排列和它做置换乘法无论左乘还是右乘都等于它本身。

3. 结合律：容易验证；

4. 逆元：容易验证，把每个循环都让它变回来即可。

群作用

分为左群作用和右群作用，下面以左群作用为例。

对于集合 \(S\) 里的任意元素 \(a\)，若存在群 \(G\) 的元素 \(g,k\) 和单位元 \(e\)，满足：

\[e \circ a = a \]

\[g \circ (k\circ a) = (g\times k) \circ a \]

则称群 \(G\) 作用于集合 \(S\)。

可能比较难理解，可以先放一放，后面会有例子。

轨道-稳定子定理

轨道

考虑一个作用在 \(X\) 上的群 \(G\)。\(X\) 中的一个元素 \(x\) 的轨道是 \(x\) 通过 \(G\) 中的元素可以转移到的元素的集合。

\(x\) 的轨道记为 \(G(x)\)，方便起见，我们用 \(g(x)\) 表示群 \(G\) 中的一个元素 \(g\) 作用域 \(x\) 的群作用的返回值，即 \(g(x) = g\circ x\)。

稳定子

\(x\) 的稳定子被定义为：\(G^x=\{g|g\in G,g(x)=x\}\)

也就是说群 \(G\) 中的元素 \(g\) 作用在 \(x\) 上，返回值还是 \(x\)。

\(\text{e.g}:\)

给定一个 \(2\times 2\) 的矩形，每个点可以使用黑白染色，这样得到的所有矩形构成的集合为 \(M\)，在后文中，我们令黑色为 \(1\)，白色为 \(0\)。

给定一个群 \(G\)，其内部元素为：\(1.\) 顺时针旋转 \(90^{\circ}\)；\(2.\) 顺时针旋转 \(180^{\circ}\)；\(3.\) 顺时针旋转 \(270^{\circ}\)；\(4.\) 顺时针旋转 \(0^{\circ}\)。可以看出，这是一个群。

我们令群 \(G\) 作用于 \(M\) 中的一个矩形中，这就是群作用，以下面这个矩形为例。

\[\binom{1 \ \ \ \ 1}{0 \ \ \ \ 0} \]

对于它来说，它的稳定子 \(G^x\) 为 \(\{\) 顺时针旋转 \(0^{\circ}\) \(\}\)。其它三个旋转后都不是它本身了。

那么，它的轨道为

\[\binom{1 \ \ \ \ 1}{0 \ \ \ \ 0},\binom{0 \ \ \ \ 1}{0 \ \ \ \ 1},\binom{0 \ \ \ \ 0}{1 \ \ \ \ 1},\binom{1 \ \ \ \ 0}{1 \ \ \ \ 0} \]

你会发现一个规律：轨道的大小与稳定子的大小的乘积刚好就是群 \(G\) 的阶。

这就是轨道-稳定子定理。

轨道-稳定子定理

\[|G^x|\times |G(x)| = |G| \]

这个我也不详细证明了，简略来说就是先证明 \(G^x\) 是 \(G\) 的一个子群，然后根据拉格朗日定理，将问题转化为证明 \([G:G^x]=G(x)\)，运用陪集的性质可得。

Burnside 定理

重头戏来了。

定义 \(G\) 为一个置换群，其作用与 \(X\)，如果 \(x,y\in X\) 在 \(G\) 的作用下可以相等即存在 \(g\in G\)，使得 \(g(x)=y\)，则定义 \(x,y\) 属于一个等价类，则不同的等价类的数量为

\[|X/G| = \frac{1}{|G|}\sum_{g\in G}X^g \]

其中，\(X^g\) 表示 \(X\) 在 \(g\) 作用下的不动点的数量。类似于稳定子，其实就是枚举 \(X\) 中的元素 \(x\)，统计 \(g(x)=x\) 的数量。

用人话说一下：一个置换群的等价类的个数等于各置换不动点个数的平均值。

证明：

由于每个元素仅属于一个轨道，轨道内部在群 \(G\) 作用下互达，所以我们得到

\[[x/G] = \sum_{x\in X}\frac{1}{[G:G^x]} \]

根据轨道-稳定子定理，我们有

\[[G:G^x] = \frac{G}{|G^x|} \]

\[|X/G|=\sum_{x\in X}\frac{G^x}{G} \]

\[|X/G|=\frac{1}{|G|}\sum_{x\in X}G^x \]

例子

光给定义可能有点懵，下面给个例子，来看看 Burnside 引理究竟是如何解决计数问题的。

\(\text{e.g}\ 1\)

首先，Burnside 一般是解决一些本质不同的计数的。

这个例子来源于here。

在 \(2\times 2\) 的方格中每个格子可以选择染上两种颜色（红色或白色）。那么总共是 \(2^4=16\) 种方案。现在问题变化一下，规定不旋转，顺时针旋转 \(90^{\circ}\)，顺时针旋转 \(180^{\circ}\)，顺时针旋转 \(270^{\circ}\) 后相同的均算成同一种方案，问总共有多少种不同的方案。

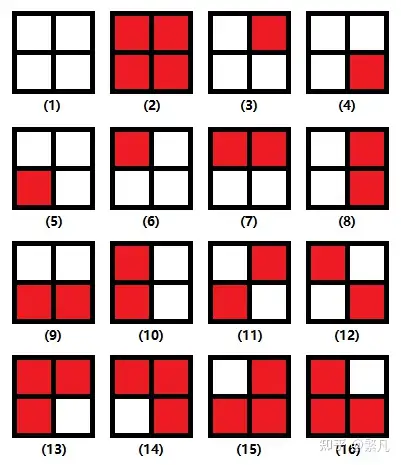
我们将每种旋转认为是一种置换，定义为 \(g_i\)，那么这个置换群 \(G\) 就包含了四种置换：\(g_1\) 到 \(g_4\)。

\(g_1\) 到 \(g_4\) 分别代表旋转 \(0^{\circ},90^{\circ},180^{\circ},270^{\circ}\)。

我们挨个计算一下：

\[\begin{aligned} &X^{g_1}=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16\}\\ &X^{g_2}=\{1,2\}\\ &X^{g_3}=\{1,2\}\\ &X^{g_4}=\{1,2,11,12\}\\ \end{aligned} \]

根据我们的公式，我们就得到

\[ans = \frac{1}{|G|}\sum_{g\in G}X^g = \frac{16+2+2+4}{4}=6 \]

这，就是 Burnside 引理。

\(\text{e.g} \ 2\)

Luogu模板题。

由题意得出，本质不同的 \(n\) 个点的环可以看作，在 \(\{\) 旋转 \(0\) 次，旋转 \(1\) 次 \(\dots\) 旋转 \(n-1\) 次\(\}\) 这个置换群 \(G\) 的作用下得到的等价类的数量。

我们定义集合 \(M\) 为 \(\{1\sim n\}\) 的所有可能排列表示初始环，显然集合的大小是 \(n^n\)。

考虑旋转 \(0\) 个的不动点的数量， 很显然：\(n^n\) 也就是所有的集合都可以。

在考虑旋转 \(k\) 个的不动点：一个环旋转 \(k\) 个后还是它本身就说明它存在一个循环节 \(a\) 使得 \(a|k\)，又因为它是循环节，所以肯定得是 \(a|n\)，所以说旋转 \(k\) 个的不动点一定是含有一个长度为 \(\gcd(k,n)\) 的循环节。

所以说对于旋转 \(k\) 个而言，确定了前 \(\gcd(k,n)\) 个，后面的就固定了，所以贡献就是 \(n^{\gcd(k,n)}\)

于是答案就是

\[\frac{1}{n}\sum_{k=1}^nn^{\gcd(k,n)} \]

之后就是拆 \(\gcd\) 了，反演的那一套整出来就行。

原式

\[\begin{aligned} &=\frac{1}{n}\sum_{d|n}n^d\sum_{k=1}^n[\gcd(k,n)=d]\\ &=\frac{1}{n}\sum_{d|n}n^d\sum_{k=1}^{\lfloor\frac{n}{d}\rfloor}[\gcd(k,\frac{n}{d})=1]\\ &=\frac{1}{n}\sum_{d|n}n^d\varphi(\frac{n}{d})\\ \end{aligned} \]

Polya 定理

有时候我们会发现有些题目如果要枚举不动点的数量的话，复杂度会炸掉，我们考虑如何不枚举不动点就能得到本质不同的方案数。

对于一个置换 \((a_1,a_2,\dots,a_n)\)，我们就是让 \(1\) 的位置变为 \(a_1\) 类似的变换，我们让 \(i\) 和 \(a_i\) 连一条边，我们发现，最后会得到若干个环，并且每个环上的颜色应该是相同的。

定义这个环的数量为 \(c(g)\)，即置换 \(g\) 的循环数，这其实就是我们上文提到的置换的循环的定理。

由此我们得到了 Polya 定理

\[Ans = \frac{1}{|G|}\sum_{g\in G}m^{c(g)} \]

这里 \(m\) 表示可用的颜色数，因为说每个环只能用一种颜色，一共 \(c(g)\) 个环，就有 \(m^{c(g)}\) 种可能。

例题

我们还是以上面提到的这个例题为例。

根据 Polya 定理我们可以得到：

不旋转

\[g_1 = \binom{1 \ 2 \ 3 \ 4}{1 \ 2 \ 3 \ 4}=(1)(2)(3)(4),c(g_1) = 4,m^{c(g_1)}=2^4 = 16 \]

顺时针旋转 \(90^{\circ}\)

\[g_2 = \binom{1 \ 2 \ 3 \ 4}{4 \ 1 \ 2 \ 3}=(1\ 4\ 3\ 2),c(g_2) = 1,m^{c(g_2)}=2^1 = 2 \]

顺时针旋转 \(180^{\circ}\)

\[g_3 = \binom{1 \ 2 \ 3 \ 4}{3 \ 4 \ 1 \ 2}=(1 \ 3)(2 \ 4),c(g_3) = 2,m^{c(g_3)}=2^2 = 4 \]

不旋转

\[g_4 = \binom{1 \ 2 \ 3 \ 4}{2 \ 3 \ 4 \ 1}=(1 \ 2 \ 3 \ 4),c(g_4) = 1,m^{c(g_4)}=2^1 = 2 \]

所以说最后的答案就是 \(\displaystyle Ans = \frac{16+2+4+2}{4} =6\)

同样是正确的。

总结

OI 中有关群论的也就这么多，重要的也就是 Burnside 引理和 Polya 定理了。跟这两个有关的题非紫即黑，不在我的能力范围之内，所以现在就当乐子学了。

标签：frac,入门,置换,times,circ,群论,binom,旋转
From： https://www.cnblogs.com/bloodstalk/p/17487516.html