错排问题
对于第n信,必然放在1~n-1号信封中。
假设n号信放在1号信封中,考虑一号信放在哪
放在n号信封中,还剩的n-2封信和信封构成了n-2的子问题f(n-2)
放在k号信封(\(2\le k< n\))f(n-1)
因为n可以放在n-1个位置。
所以(f(n-1)+f(n-2))*(n-1)
P1595 信封问题
板子题,不多说了
P4071 [SDOI2016]排列计数
简而言之就是选择m个位置不错排,n-m个位置错排
P2822 [NOIP2016 提高组] 组合数问题
杨辉三角版二维前缀和预处理即可。记得处理细节
卢卡斯定理
\(C_n^m \equiv C_{n/d}^{m/d}\times C_{n\%d}^{m\%d}\pmod p\) ,p为质数
扩展卢卡斯
未讲,待填,省队知识。
技巧练习
例一:
\(n\)个询问,求 \(C_b^a\pmod p\)
数据范围:\(n\le 10^5\)且\(\ a,b\le 10^3\)
数字三角形即可
例二:
\(n\)个询问,求 \(C_b^a\pmod{10^9+7}\)
数据范围:\(n\le 10^5\)且\(\ a,b\le 10^5\)
预处理阶乘及其逆元
例三:
\(n\)个询问,求 \(C_b^a\pmod{p}\),\(p\) 为质数
数据范围:\(n\le 20\)且\(\ a,b\le 10^{18}\)
使用卢卡斯即可
例四:
\(n\)个询问,求 \(C_b^a\)
数据范围:\(n\le 10^5\)且\(\ a,b\le 5\times 10^3\)
由 \(C_n^m=\frac{n!}{(n-m)!m!}\) ,而这个数又必须是整数
根据阶乘分解,我们可以将三个阶乘的质因数分解,分子质因数分解后减去分母质因数分解。
剩下的次幂数还原相乘即可。
于是只需要写大数乘法。
卡特兰数
设卡特兰数的第 \(n\) 项为 \(Cat_n\)
卡特兰数前几项(从第0项开始):1, 1, 2, 5, 14, 42, 132, 429
\[Cat_n=\frac{C_{2n}^n}{n+1} \]我们来用这道题来解释卡特兰数。
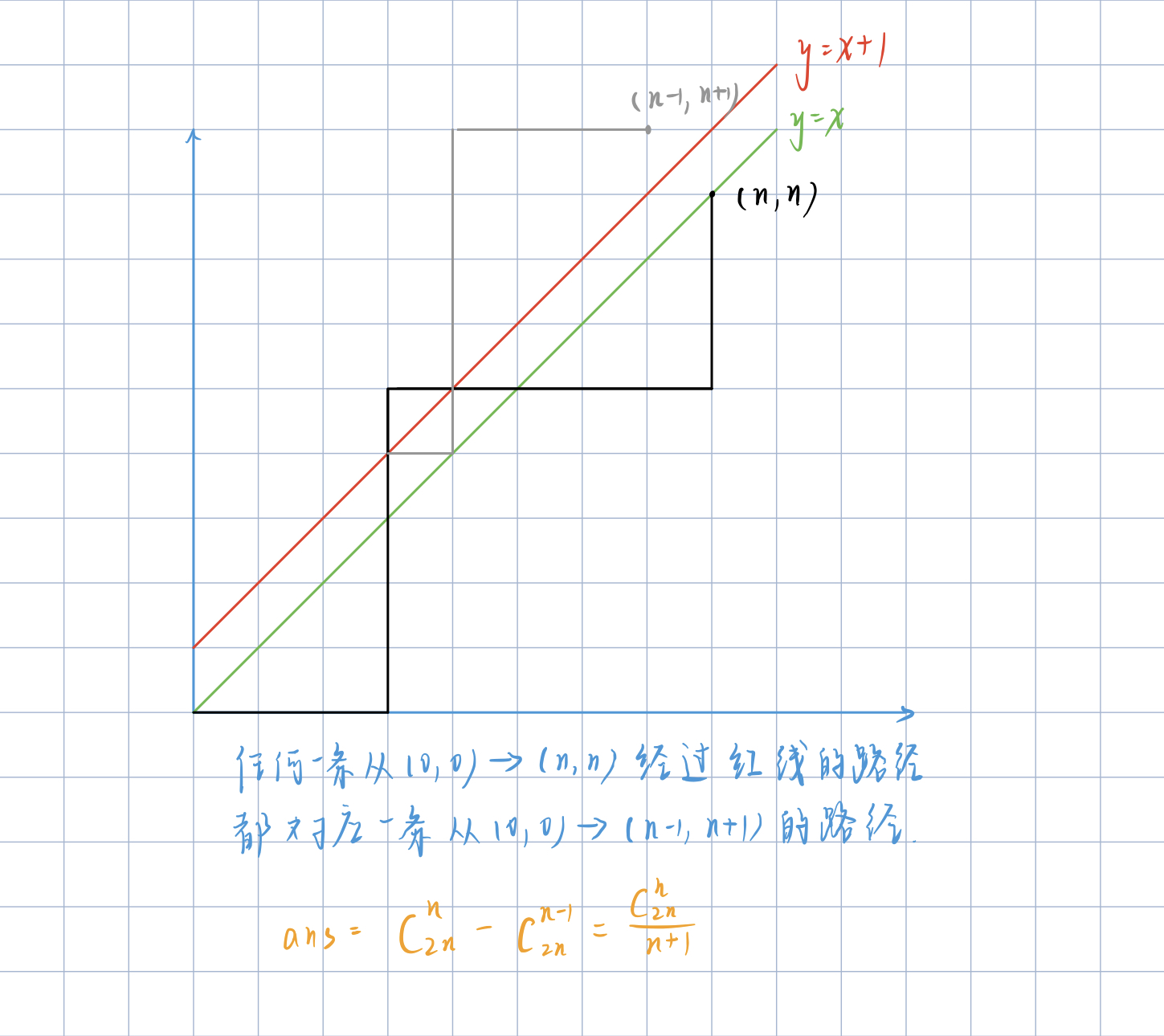
绿色线是边长为n的正方形对角线,此时y=x,若某点在绿线上方,则不符合条件,将此点及后面经过的点关于y=x+1对称,一定会经过点(n-1,n+1)。
这一步的目的其实是区分符合与不符合条件的路径。
换句话说,所有不符合条件的点,一定会经过y=x+1,所有符合条件的点,都不会经过(废话嘛,经过了就y>x了)。
组合笔记&杂题
排列:从 \(n\) 个物品选 \(k\) 个,问有多少种顺序,记 \(A_n^k\)
\[A_n^k=\frac{n!}{(n-k)!}=n\times (n-1)\times (n-2)\cdots (n-k+1) \]组合:从 \(n\) 个物品选 \(k\) 个,问有多少种方案,记 \(C_n^k\),也记为 $\binom{n}{k} $ 。
\[C_n^k=\frac{A_n^k}{A_k^k}=\frac{n!}{(n-k)!k!}=\frac{n\times (n-1)\times (n-2)\cdots (n-k+1)}{k!} \]\(C_n^0=1\) ,\(C_n^1=n\) ,\(C_n^2=\frac{n(n-1)}{2}\) ,\(C_n^k=C_n^{n-k}\)
给定三个正整数 \(N,L\) 和 \(R\),统计长度在 \(1\) 到 \(N\) 之间,元素大小都在 \(L\) 到 \(R\) 之间的单调不降序列的数量。输出答案对 \(10^6+3\) 取模的结果。
\(1\le N,L,R\le 10^9,1\le T\le 100\),输入数据保证 \(L\le R\)。
设目标序列为 \(a\) 。
\[L\le a_1\le a_2\cdots\le a_n\le R \]我们来做一个映射。
\[0\le a_1\le a_2\cdots\le a_n\le R-L \]设 \(t\) 是 \(a\) 的差分序列。则 \(t_1=a_1,t_2=a_2-a_1\cdots t_n=a_n-a_{n-1}\)
所以
\[x_1+x_2+x_3\cdots x_n\le R-L \]因为是不大于,就设一个 \(x_{n+1}\) ,使 \({x_1+x_2+x_3\cdots x_{n+1}}=R-L\)
(简单来说 \(x_{n+1}\) 就是去掉不大于……)
所以,就相当于有 \(R-L\) 个苹果,分成 \(n+1\) 份,每份可以等于0。
直接可以做允许为0的插板即可。
\[C_{R-L-1+n}^{n} \](好吧我承认我一开始没看到长度在 \(1\) 到 \(N\) 之间)
于是现在就变成求
\[\sum_{i=1}^{i\le n} C_{R-L+i+1}^{i} \]杂项
等比数列:\(S_n=a_0\frac{q^n-1}{q-1}\)
n以内质数个数大概是 \(\frac{n}{\ln\ n}\),插一条证明(虽然这篇文章大部分都是在讲别的……)
在12e9范围内,1N中任何数的不同质因子都不会超过10个,且所有质因子的指数总和不超过30
证明:
因为最小的11个质数的乘积大于2e9,且2^31>2e9,所以成立
\(a\bmod b=a-\lfloor \frac{a}{b}\rfloor\times b\)
标签:10,le,frac,times,cdots,排列组合,卡特兰 From: https://www.cnblogs.com/lldxjw/p/17568549.html