首页 > 其他分享 >排列组合的应用

排列组合的应用

时间：2023-05-08 15:44:18浏览次数：53  
标签：nums self results dfs start 应用 path 排列组合

目录

力扣上涉及排列组合相关的题目如下：

序号 题目 备注
1 39. 组合总和 数组无重复元素，每个元素可以多次重复选择
2 40. 组合总和 II 数组有重复元素，每个元素只能选择一次
3 216. 组合总和 III 数组无重复元素，每个元素只能选择一次
4 78. 子集 数组无重复元素，每个元素至多能选择一次，组合不能重复
5 90. 子集 II 数组有重复元素，每个元素至多能选择一次，组合不能重复
6 77. 组合 数组无重复元素，每个元素至多能选择一次，组合长度固定且不能重复
7 46. 全排列 数组无重复元素，每个元素只能选择一次
8 47. 全排列 II 数组有重复元素，每个元素只能选择一次，组合不能重复

应用

应用1：Leetcode.39

题目

39. 组合总和

输入：\(candidates = [2,3,6,7]\), \(target = 7\)
输出：\([[2,2,3],[7]]\)

分析

我们直接对每一个数字都进行回溯遍历，找到所有满足条件的路径即可。

题目中的数组无重复元素，并且每一个元素可以多次重复选择。

回溯的时候，我们使用数组的索引作为遍历条件，退出条件为：当已经选择的元素之和等于目标值，或者，已经遍历的完数组中的所有元素。

对于每一个数字，都有两种策略：选择 和 不选择：

  • 如果选择当前数字，因为同一个元素可以重复选择，所以，索引不变；

  • 如果不选择当前数字，则索引加一，即继续向后面枚举数组中的剩余元素。

以题目中的用例为例，其回溯的过程如下：

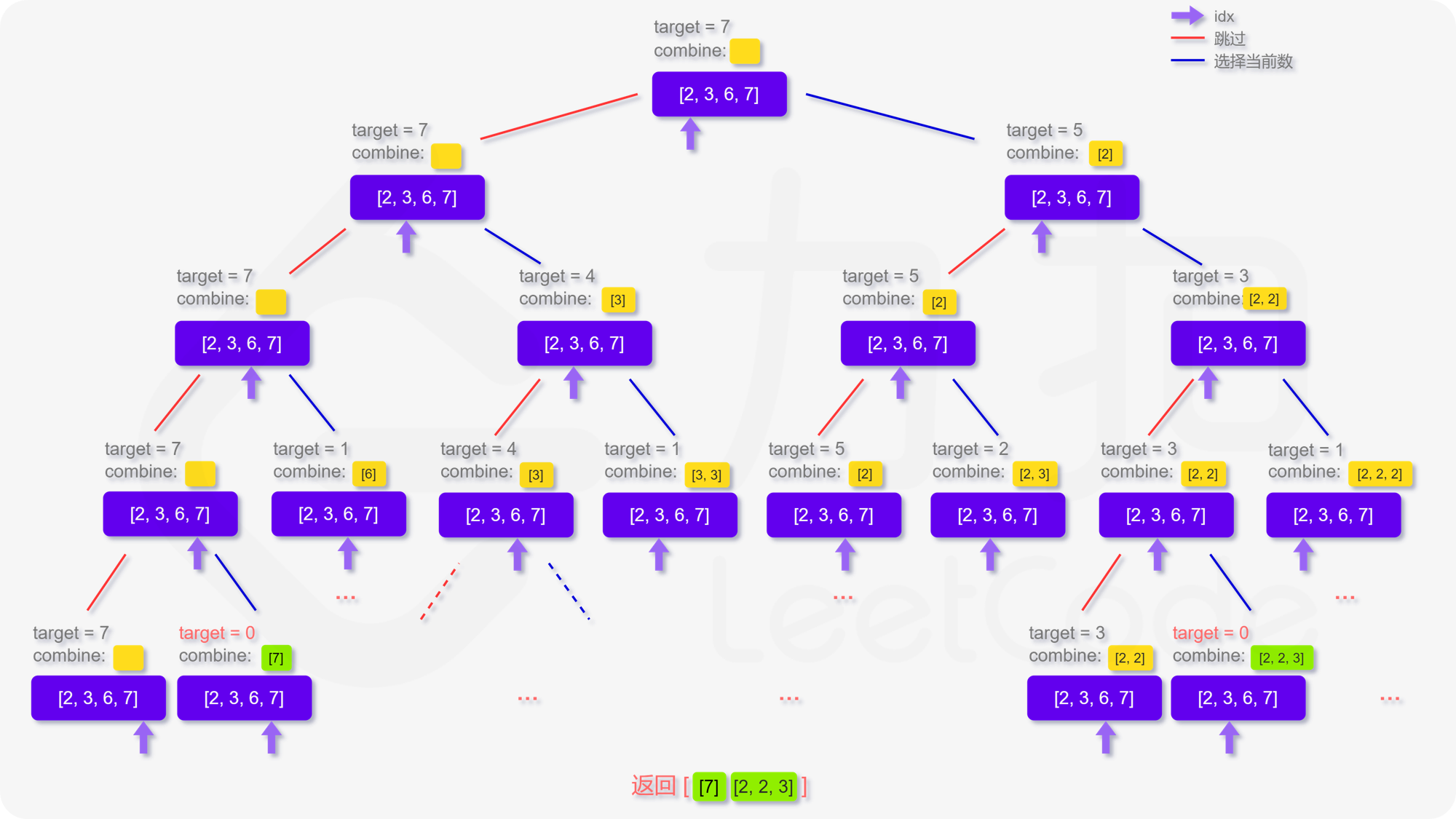
image

代码实现

方法一

def dfs(candidates: List, target: int, results: List, path: List, start: int):
    # 如果已经到达决策树的底层，则停止回溯
    if start == len(candidates):
        return

    # 如果满足回溯条件，则保存结果
    if target == 0:
        results.append(path[:])
        return

    # 1.如果不选择当前数字
    dfs(candidates, target, results, path, start + 1)

    # 2.如果选择当前数字
    if target - candidates[start] >= 0:
        # 做选择
        path.append(candidates[start])
        # 继续回溯
        dfs(candidates, target - candidates[start], results, path, start)
        # 撤销选择
        path.pop()

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        results = list()
        path = list()
        dfs(candidates, target, results, path, 0)
        return results

方法二

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        results = list()
        path = list()
        self.dfs(candidates, target, results, list(), 0, 0)
        return results

    def dfs(self, candidates, target, results, path, total, start):
        if total > target:
             return

        if total == target:
            results.append(list(path))
            return 

        for i in range(start, len(candidates)):
            path.append(candidates[i])
            self.dfs(candidates, target, results, path, total + candidates[i], i)
            path.pop()
        return

应用2：Leetcode.40

题目

40. 组合总和 II

分析

题目中的数组有重复元素，并且每一个元素只能选择一次。

直接对每一个数字进行回溯遍历，枚举所有的选择。

由于数组中可能存在重复元素，所以，可以通过预先对数组排序，将相同的元素排在一起，递归时跳过相同元素，通过这种方式去重，从而避免不同的组合选择相同的元素。

回溯的时候，我们使用数组的索引作为遍历条件，每次回溯后，下一次回溯就从剩余的元素中选择。

退出条件为：当已经选择的元素之和等于目标值，或者，已经遍历的完数组中的所有元素。

以如下用例为例：

\(candidates = [1, 1, 2]\), \(target = 3\)

其回溯过程如下：

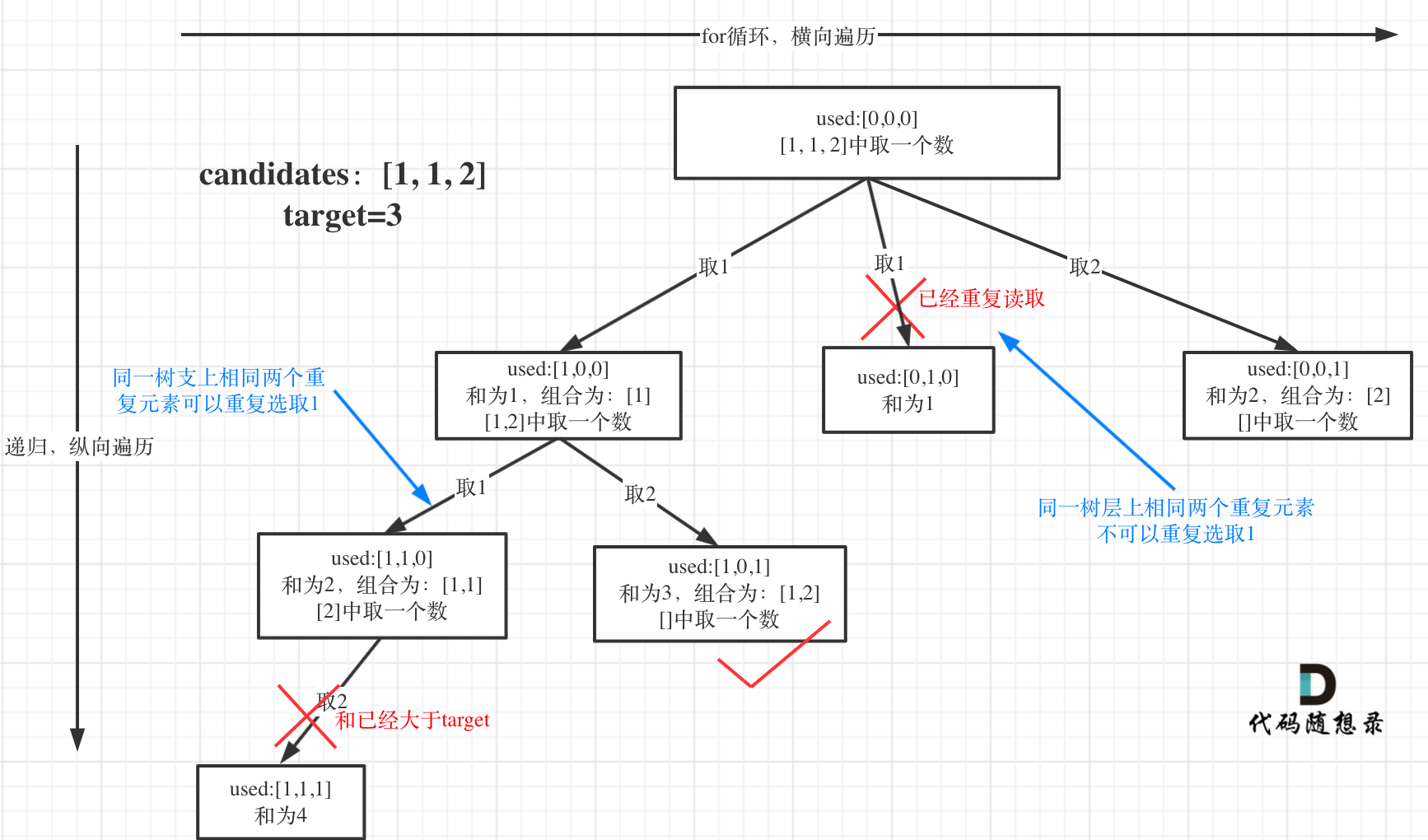
image

代码实现

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        if not candidates:
            return []

        results = list()
        path = list()

        self.dfs(sorted(candidates), target, path, results, 0)
        return results

    def dfs(self, candidates: List[int], target: int, path: List[int], results: List[List[int]], start: int):
        if target == 0:
            results.append(path[:])
            return

        # 从剩余元素中进行选择
        for i in range(start, len(candidates)):
            if target < candidates[i]:
                break
            # 去重：跳过同一层已经使用过的元素
            if i > start and candidates[i] == candidates[i - 1]:
                continue

            path.append(candidates[i])
            self.dfs(candidates, target - candidates[i], path, results, i + 1)
            path.pop()

应用3：Leetcode.216

题目

216. 组合总和 III

分析

题目可以转换为：从数组 \(nums = [1,2,3,4,5,6,7,8,9]\) 中，选择 \(k\) 个数，使其和为 \(n\)。

即数组无重复元素，并且每一个元素只能选择一次。

直接对每一个数字进行回溯遍历，枚举所有的选择。

我们使用数组的索引作为遍历条件，每次回溯后，下一次回溯就从剩余的元素中选择，避免重复选择相同元素。

代码实现

方法一

MIN_NUM = 1
MAX_NUM = 9

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        results = list()
        self.dfs(k, n, results, list(), MIN_NUM, 0)
        return results

    def dfs(self, k, n, results, path, start, total):
        if total == n and len(path) == k:
            results.append(path[::])
            return

        if start > MAX_NUM or len(path) > k:
            return

        # 不选择当前数字
        self.dfs(k, n, results, path, start + 1, total)

        # 选择当前数字
        path.append(start)
        self.dfs(k, n, results, path, start + 1, total + start)
        path.pop()

方法二

MIN_NUM = 1
MAX_NUM = 9

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        results = list()
        self.dfs(k, n, results, list(), MIN_NUM, 0)
        return results

    def dfs(self, k, n, results, path, start, total):
        if total > n or len(path) > k:
            return

        if len(path) == k:
            if total == n:
                results.append(path[::])
            return

        for i in range(start, MAX_NUM + 1):
            path.append(i)
            self.dfs(k, n, results, path, i + 1, total + i)
            path.pop()

应用4：Leetcode.78

题目

78. 子集

分析

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点。

其实子集也是一种组合问题，因为它的集合是无序的，子集 \(\{1,2\}\) 和子集 \(\{2,1\}\) 是一样的。

那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！

以如下用例为例：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

求子集抽象为树型结构，如下：

image

可以看出遍历这棵树的时候，把路径上所有的节点都记录下来，就是要求的子集集合。

代码实现

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        results = list()
        self.dfs(0, nums, list(), results)
        return results

    def dfs(self, start, nums, path, results):
        if start == len(nums):
            results.append(list(path))
            return

        path.append(nums[start])
        self.dfs(start + 1, nums, path, results)
        path.pop()

        self.dfs(start + 1, nums, path, results)
        return

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        results = list()
        self.dfs(nums, results, list(), 0)
        return results

    def dfs(self, nums, results, path, start):
        results.append(list(path))

        # 可要可不要，因为变量start最多为len(nums)，当start=len(nums)，下面的for循环不会执行，递归已经结束了
        if start == len(nums):
            return

        for i in range(start, len(nums)):
            path.append(nums[i])
            # 注意start从i+1开始，保证元素不重复取
            self.dfs(nums, results, path, i + 1)
            path.pop()
        return

应用5：Leetcode.90

题目

90. 子集 II

分析

数组有重复元素，每个数可以选择，可以不选择，并且每一个元素至多只能选择一次，选择的组合不能有重复。

由于组合不能有重复，我们首先对数组排序，用于回溯的时候去重。

这里我们需要用一个 \(visited\) 数组记录已经访问过的元素，用于回溯时，跳过已经选择过的元素。同时，对于未选择的元素，如果它与前一个未选择过的元素相同，则跳过当前元素，这样，就可以避免出现相同的组合。

代码实现

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return list()

        results = list()
        nums.sort()
        visited = [False] * len(nums)
        self.dfs(nums, results, list(), visited, 0)
        return results

    def dfs(self, nums, results, path, visited, start):
        results.append(list(path))

        for i in range(start, len(nums)):
            if visited[i]:
                continue

            if i > 0 and nums[i] == nums[i - 1] and not visited[i - 1]:
                continue

            path.append(nums[i])
            visited[i] = True
            self.dfs(nums, results, path, visited, i)
            path.pop()
            visited[i] = False
        return

也可以去掉 \(visited\) 数组：

class Solution:
    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return list()

        results = list()
        nums.sort()
        self.dfs(nums, results, list(), 0)
        return results

    def dfs(self, nums, results, path, start):
        results.append(list(path))

        for i in range(start, len(nums)):
            if i > start and nums[i] == nums[i - 1]:
                continue

            path.append(nums[i])
            # 去掉visited数组后，注意start从i+1开始，保证元素不重复取
            self.dfs(nums, results, path, i + 1)
            path.pop()

        return

应用6：Leetcode.77

题目

77. 组合

分析

以如下用例为例：

输入：n = 4, k = 2
输出：[[2,4], [3,4], [2,3], [1,2], [1,3], [1,4],]

其搜索过程如下：

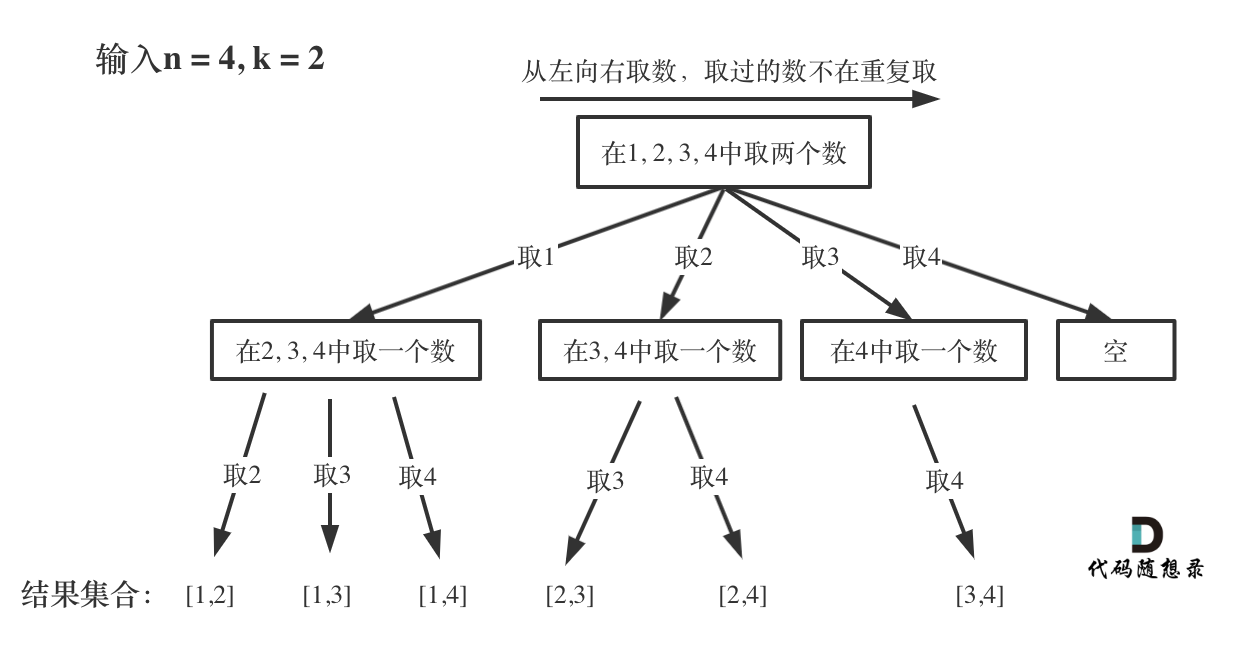
image

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现 \(n\) 相当于树的宽度，\(k\) 相当于树的深度。

图中每次搜索到了叶子节点，我们就找到了一个结果，相当于只需要把达到叶子节点的结果收集起来，就可以求得 \(n\) 个数中 \(k\) 个数的组合集合。

代码实现

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        results = list()
        self.dfs(1, n, k, list(), results)
        return results

    def dfs(self, start, n, k, path, results):
        if len(path) == k:
            results.append(list(path))
            return 

        if len(path) + n - start + 1 < k:
            return

        # 选择当前位置
        path.append(start)
        self.dfs(start + 1, n, k, path, results)
        path.pop()

        # 不选择当前位置
        self.dfs(start + 1, n, k, path, results)
        return

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        results = list()
        self.dfs(n, k, results, list(), 1)
        return results

    def dfs(self, n, k, results, path, start):
        if len(path) == k:
            results.append(list(path))
            return

        # 剪枝：区间长度+已经选择的元素小于k，就不再继续递归遍历
        if len(path) + n - start + 1 < k:
            return

        for i in range(start, n + 1):
            path.append(i)
            self.dfs(n, k, results, path, i + 1)
            path.pop()

应用7：Leetcode.46

题目

46. 全排列

分析

数组无重复元素，并且每一个元素只能选择一次。

这里我们需要用一个 \(visited\) 数组记录已经访问过的元素，避免在一个组合中重复选择相同的元素。

我们使用 \(visited\) 作为遍历条件，每次回溯后，下一次回溯就从没有访问过的的元素中选择，避免重复选择相同元素。

代码实现

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        results = list()
        visited = [False] * len(nums)
        self.dfs(nums, visited, results, list())
        return results

    def dfs(self, nums, visited, results, path):
        if len(path) == len(nums):
            results.append(list(path))
            return

        for i in range(len(nums)):
            if visited[i]:
                continue
            visited[i] = True
            path.append(nums[i])
            self.dfs(nums, visited, results, path)
            path.pop()
            visited[i] = False

应用8：Leetcode.47

题目

47. 全排列 II

分析

数组有重复元素，并且每一个元素只能选择一次，选择的组合不能有重复。

由于组合不能有重复，我们首先对数组排序，用于回溯的时候去重。

这里我们需要用一个 \(visited\) 数组记录已经访问过的元素，用于回溯时，跳过已经选择过的元素。同时，对于未选择的元素，如果它与前一个未选择过的元素相同，则跳过当前元素，这样，就可以避免出现相同的组合。

如后面的代码实现所示，下面两种判断条件都能实现组合的去重：

  • 树枝去重

    表示在决策树的树枝上去重，这种复杂度更高。

    if i >= 1 and nums[i] == nums[i - 1] and visited[i - 1]:
    continue

    已经访问过的元素，一定是路径上的元素，当重复元素较多的时候，重复的元素会产生很多重复的组合，会产生很多相同的树枝。

    具体去重的过程如下：

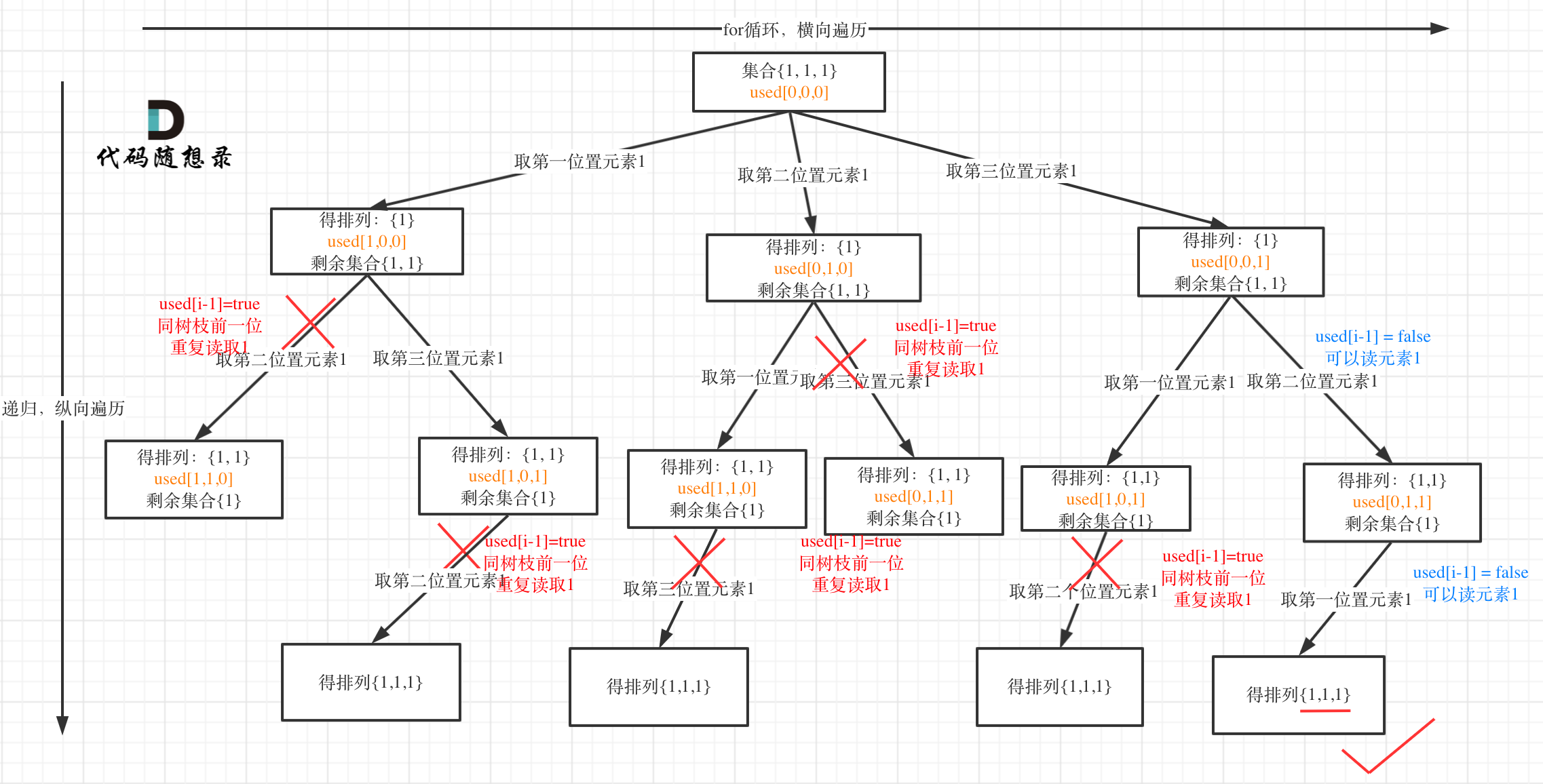
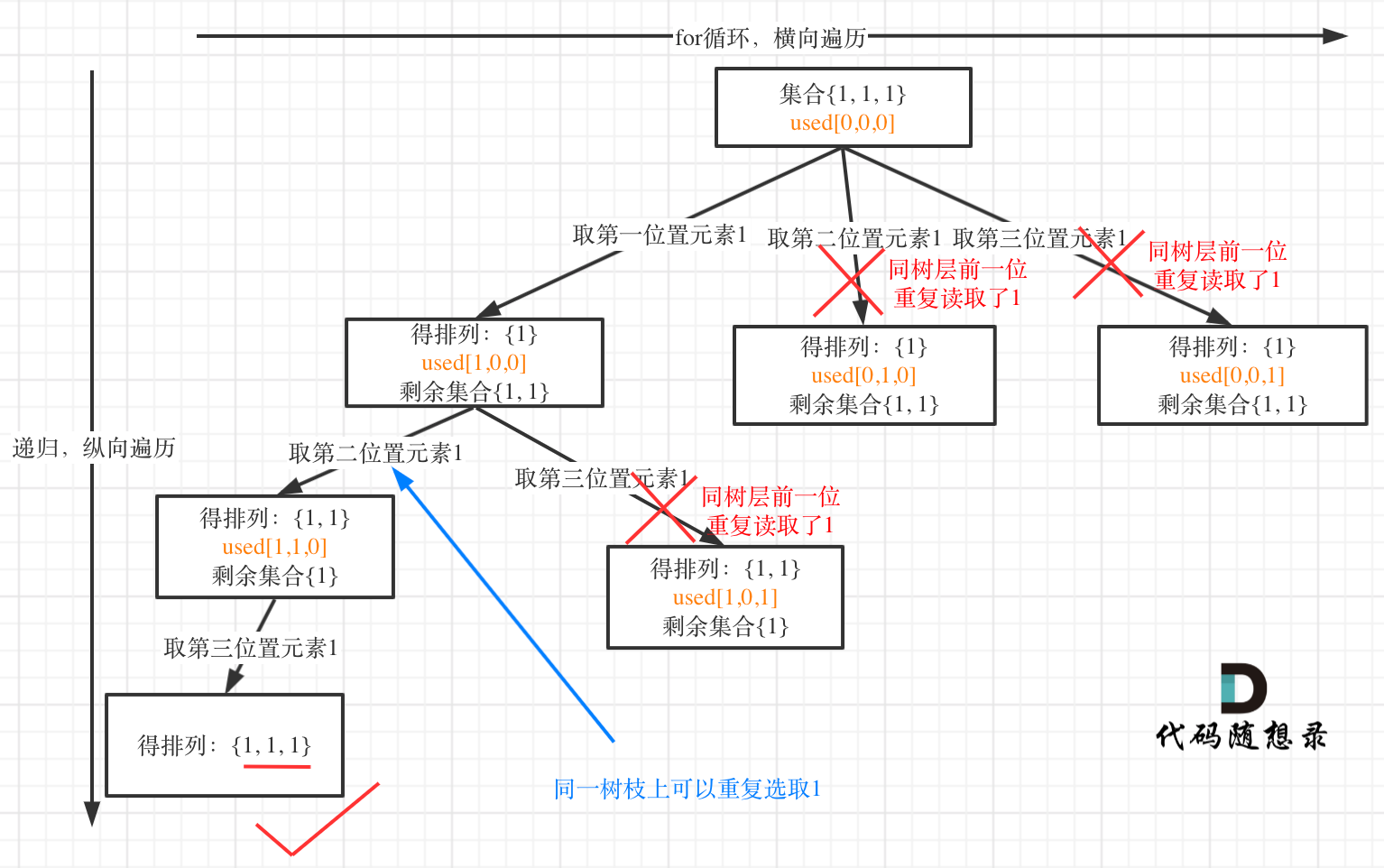
    image

  • 同层去重

    表示在决策树的同层去重，这种复杂更低，效率更高。

    if i >= 1 and nums[i] == nums[i - 1] and not visited[i - 1]:
    continue

    在源头就去掉重复的元素，如果当前路径上的元素与其他组合的元素相同，从这个节点停止遍历子节点。

    具体去重的过程如下：

    image

代码实现

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        if not nums:
            return []
        results = list()
        visited = [False] * len(nums)
        nums.sort()  # 对数组排序，便于回溯时去重
        self.dfs(nums, visited, results, list())
        return results

    def dfs(self, nums, visited, results, path):
        if len(path) == len(nums):
            results.append(list(path))
            return

        for i in range(len(nums)):
            # 跳过已经选择过的元素
            if visited[i]:
                continue

            # 去重：如果当前元素未被访问，且与前一个未选择过的元素相同，则跳过
            if i >= 1 and nums[i] == nums[i - 1] and not visited[i - 1]:
                continue

            path.append(nums[i])
            visited[i] = True
            self.dfs(nums, visited, results, path)
            path.pop()
            visited[i] = False
        return

参考：

标签：nums,self,results,dfs,start,应用,path,排列组合
From： https://www.cnblogs.com/larry1024/p/17373531.html

相关文章

  • 瑞芯微RK3568开发板在智慧交通行业中的应用方案
    智能交通安全监测系统是通过利用高性能处理器和先进的图像处理算法，实现对交通场景的实时监测、分析和预警，以提高交通安全水平。以下是基于RK3568处理器的智能交通安全监测系统产品的应用方案：视频采集与处理：     使用RK3568处理器搭配高清摄像头，进行交通场景的视频采集。R......
  • 封闭式开关柜在线测温技术的应用
    安科瑞虞佳豪传统的测温方式有红外点温仪测温、红外热成像仪测温、试温腊片等方式，这几种方式无法实现24小时全天候测量工作，特别是在一些特定场合下，分散监测、环境封闭、有高压电，无法进行有效测温。在电力系统设备在长期的运行中，往往容易产生老化或过热现象，这些现象如果没有及时......
  • nacos配置自动刷新（不重启应用）
    （一）背景我们平常的开发中经常会遇到需要修改配置的情况，但是又不希望重启应用。以nacos为例子，哪些情况修改完配置不重启应用就可以自动生效呢？下面开始做个简单的测试（二）测试@value注解 @Value("${testa.name}")privateStringname; 经测试，每次在nacos修改完不重启应用是......
  • C/C++二叉树应用[2023-05-08]
    C/C++二叉树应用[2023-05-08]湖南应用技术学院实验（训）报告课程名称 数据结构与算法 课程代码 221031203 成绩评定 学院 信息工程学院 专业 物联网工程 指导老师 聂作财学生姓名 xxxx 学号 xxxxx 班级 物联xxxx实验地点 实验日期 年月日小组成员 无实验类型 □验......
  • AI 在 API 设计中的应用：如何利用 Al 快速实现 API 开发和测试
    一、引言在当今互联网技术的快速发展中，API成为了越来越多的软件和系统之间交互的核心方式，而API的质量和效率对于软件的开发和运维都至关重要。为了提高API的设计、开发、测试和运维的效率和质量，越来越多的公司开始使用智能API协作平台，EolinkApiKit就是代表之一。Eolink......
  • AspNetCoreRateLimit应用于MVC项目求助
    AspNetCoreRateLimit应用于MVC项目求助前言之前发过一篇文章：.NETCoreWebApi接口ip限流实践-妙妙屋（zy）-博客园(cnblogs.com)然后应用在前后端分离项目这个组件是非常好用的。但应用于不分离的项目，比如我的个人博客就有点麻烦。就是我的需求是评论接口限流，然后触发限流后......
  • IOS6.0 应用内直接下载程序&n…
    闲来没事看了篇文章应用内创建应用商店环境，不跳转AppStore.先武断的想一句：放屁。然后好奇的进去看看，原来是IOS6.0的新特性，顿感惭愧。研究下SKStoreProductViewController类是UIViewController的子类,如果你对viewcontroller比较熟悉的话，那SKStoreProductViewController使用起来......
  • kali中使用exe文件安装应用程序
    kali中直接打开exe文件是会报错的，因此需要安装wine插件才能使用exe文件安装应用程序。1、终端使用root账号登录，输入sudodpkg--add-architecturei386开启i386支持。2、使用vim/etc/apt/sources.list命令打开kali下载安装的源，往里面写入wine的官网debhttps://dl.winehq.org/w......
  • Xshell7提示：要继续使用此程序,您必须应用最新的更新或使用新版本
    今天打开xshell的时候，报出问题，需要更新到新版本：Xftp7也是无法直接打开。解决方案：1.新建xshell新版本补丁.bat##################################begin####################@echooff%1mshtavbscript:CreateObject("Shell.Application").ShellExecute("cmd.exe","/c%~s......
  • 图的应用（408）
    最小生成树定义：生成树包含连通图的所有顶点，以及n-1条边。最小的含义是，边权和最小性质：1、最小生成树的树形不唯一。如果图的每条边权都互不相等的时候，该最小生成树的唯一的。2、最小生成树的边权和是唯一的且最小的。3、边数为顶点数-1通用算法：Prim算法：1）从任意一个顶点开始......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99