排列组合是数学中一项非常重要、基础的内容，可以解决许多与计数有关的问题。

让我们先从最基本的数数学起。

前置知识

加法原理

假设你现在有 \(a_0\) 个物品，所有物品互不相同。你要从中拿一个物品出来，拿出的物品可能有几种？

显然是 \(a_0\) 种，因为每一个物品互不相同，每一个物品都可能被拿到。

假设再放进来 \(a_1\) 种物品，所有的物品仍然互不相同。继续从这些物品中拿一个出来，现在又有几种可能被拿出的物品？

显然是 \(a_0+a_1\) 种，因为所有物品互不相同。

同理，之后又放进来了 \(a_2,a_3,a_4\cdots\) 个物品，则以上问题的答案为 \(a_0+a_1+a_2+\cdots +a_n\)。

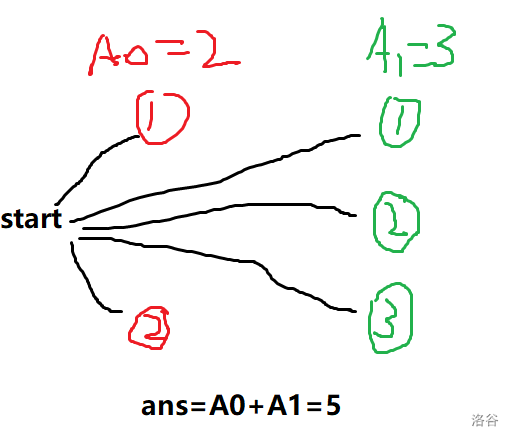
这是加法原理，即多种事件并列，情况数量相加。

乘法原理

你一开始仍然有不同 \(a_0\) 个物品，此时仍然有 \(a_0\) 种不同的物体可能被被选中。

又有 \(a_1\) 个不同物品，所有物体均不一样。求从 \(a_0\) 个物体中选出一个物体并同时从 \(a_1\) 个物体中选出一个物体，被选中的两个物体有多少种不同的可能？

先钦定 \(a_0\) 个物体中已经选好了一个，这时 \(a_1\) 个物体都有可能被选到，情况数是 \(a_1\) 种。再因为 \(a_0\) 个物体每一个都不一样，所以答案是 \(a_0\times a_1\)。

同理，有 \(n+1\) 堆物品，所有物品互不相同且 \(n+1\) 堆物品分别有 \(a_0,a_1,\cdots,a_n\)。则每堆物品中各拿一个，能选出的方案不同数有 \(a_0\times a_1\times \cdots\times a_n\)。

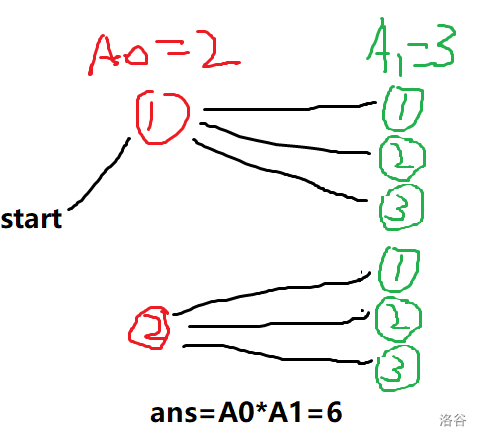
这是乘法原理，多种事件按顺序发生，情况数量相乘。

基础概念

排列数

从 \(n\) 个不同的物体中选出 \(m\) 个物体，考虑顺序（即a,b与b,a不为一种方案），有多少种方案？

选第一个物体时有 \(m\) 种选择；选第二个物体时，由于已经被选走了一个物体，所以还剩 \(m-1\) 种选择；选择第 \(i\) 个物体时，已经被选走了 \(i-1\) 个物体，还剩下 \(m-(i-1)\) 种选择。

根据乘法原理，先选第一个物体，再选第二个物体，...。所以答案为 \(n\times (n-1)\times (n-2)\times\cdots\times (n-m+1)\)。

这个问题的答案被称为 \(A^m_n\)，也就是排列数。即 \(A^m_n\) 的含义为从 \(n\) 个物体中选出 \(m\) 个物体，考虑顺序（物体互不相同） 的方案数。

一类特殊的排列数是 \(A^n_n\) ，即全排列， \(A^n_n=n\times (n-1)\times\cdots\times 1\)，也就是 \(n!\)。可以理解为序列 \(1,2,3,\cdots,n\) 有多少种不同的排列方式。\(A_m^n\) 可以通过阶乘表示，即 \(A_n^m=\frac{n!}{(n-m)!}\) 。

组合数

从 \(n\) 个不同的物体中选出 \(m\) 个物体，不考虑顺序（即a,b与b,a为一种方案），有多少种方案？

这个问题与上面的问题很像，只是选出来之后不考虑内部顺序。考虑从上面那个问题转移过来，因为一个有 \(m\) 个物品的选择方案，考虑顺序有 \(m!\) 种排列方法（即上面的全排列），而这 \(k!\) 种顺序都会被考虑一次，但我们只要 \(1\) 次，所以将先前的方案数 \(\div m!\)，也就是 \(\frac{A^m_n} {m!}\)。我们把这个数定义为 \(C^m_n\),或 \(\binom{n}{m}\)，一般使用 \(\binom{n}{m}\) 来表示组合数，\(\binom{n}{m}=\frac{A^m_n} {m!}=\frac{n!}{m!(n-m)!}\)。

组合数也可以用另一种方法来表示：\(\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1}\)。