对 Alex_wei 博客的抄写。

复数与单位根

复数

跳出实数域 \(\mathbb{R}\)，定义 \(i^2 = -1\)，即 \(i=\sqrt{-1}\)，并在此基础上定义复数 \(a+bi\)，其中将 \(b\not= 0\) 的称为虚数。复数域记为 \(\mathbb{C}\)。

我们根据上面的定义一下复数的四则运算。

加法：\((a+bi)+(c+di) = (a+c)+(b+d)i\)
减法：\((a+bi)-(c+di) = (a-c)+(b-d)i\)
乘法：\((a+bi)(c+di) = (ac-bd)+(ad+bc)i\)
除法：\(\displaystyle \frac{a+bi}{c+di}= \frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i\)

复数的除法其实是一个分母有理化的过程，我们乘上一个分母的共轭复数，就是实部相等，虚部为相反数的复数，来使得分母有理化。

复平面与棣莫弗定理

描述一个复数 \(a+bi\) 需要两个值 \(a\) 和 \(b\)，其实 \(a\) 表示实部，\(b\) 表示虚部。这表明我们可以把它放到平面直角坐标系上进行描述，称为复平面。其在复平面上的坐标为 \((a,b)\)，实部 \(a\) 为横坐标，虚部 \(b\) 为纵坐标。

一个复数可以唯一对应一个复平面上的向量。我们将向量起点平移至远点，那么它的重点就指向与其对应的复数。我们把平面向量的一些性质应用到复平面上，就能得到一些定义：

定义复数 \(z=a+bi\) 的模为 \(|z|=\sqrt{a^2+b^2}\)。
定义复数 \(z=a+bi\) 的辐角为 \(\text{Arg} \ z=\theta\)，其中 \(\tan \theta=\frac{a}{b}\)。满足 \(-\pi < \theta \leq \pi\) 的 \(\theta\) 称为辐角主值，记作 \(\arg z\)，即 \(\arg z =\arctan\frac{a}{b}\)。说这么多其实就是这个向量与 \(x\) 轴的夹角。
辐角确定了 \(z\) 所在的直线，模确定了 \(z\) 在直线上的长度。有了这两个，我们可以用另一种方法来描述复数。

根据 \(z = a+bi\) 的模 \(r\) 和辐角 \(\theta\)，可知 \(z\) 的实部 \(a=r\cos\theta\)，虚部 \(b=r\sin\theta\)，据此我们定义复数的三角形式 \(z = r(\cos\theta + i\sin\theta)\)。

利用 \(\sin,\cos\) 的和角公式可得 \(z_1z_2 = r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2))\)。该等式称为棣莫弗定理，它说明复数相乘，模长相乘，辐角相加。

根据棣莫弗定理，我们得到对于虚数单位 \(i\) 的一种直观理解：将一个复数 \(z\) 乘以 \(i\) 相当于将其逆时针旋转 \(\frac{\pi}{2}\) 弧度。我们再看 \(i\) 在复平面上是在 \((0,1)\) 的位置，它其实就是让 \(1\) 逆时针旋转了 \(\frac{\pi}{2}\) 弧度。所以说，\(i\) 就代表了旋转。

单位根

当 \(r=1\) 时，\(z=\cos\theta + i\sin\theta\) 在单位圆上。此时根据棣莫弗定理有 \(z^n = \cos(n\theta)+i\sin(n\theta)\)，这个式子很美妙，它在复数旋转和复数乘法之间构建了桥梁：\(z\) 的 \(n\) 次幂相当于从 \((1,0)\) 开始，以 \(z\) 辐角的角度在单位圆上旋转 \(n\) 次得到的结果，称为将 \(z\) 旋转 \(n\) 次。

引用一下 wls 的图片。

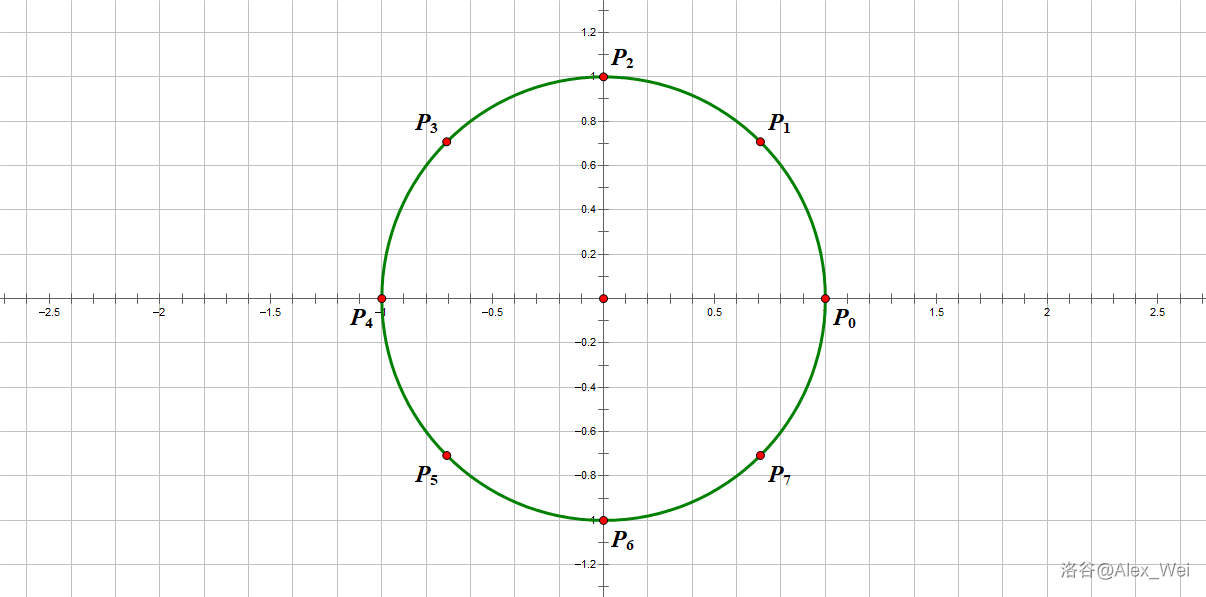
在这里，我们将单位圆 \(n\) 等分，取任意 \(n\) 等分点 \(P_k(0\leq k < n)\)，将其旋转 \(n\) 次均得到 \(1\)，也就是 \(P_k^n = 1\)，我们探究一下为什么。

因为 \(P_k\) 相当于从 \(1\) 开始在单位圆上旋转 \(\frac{2k\pi}{n}\) 弧度，因此 \(P_k = \cos(\frac{2k\pi}{n})+i\sin(\frac{2k\pi}{n})\)，你会发现旋转 \(n\) 次后，\(P_k^n = \cos(2k\pi)+i\sin(2k\pi) = 1\)。我们称所有 \(P_k\) 为 \(n\) 次单位根，将 \(P_1\) 记作 \(\omega_n\)，则有 \(P_k = P_1^k = \omega_n^k\)。

根据 \(P_k^n=1\) 我们可知道任意 \(n\) 次单位根 \(\omega_n^k\) 均为 \(x^n = 1\) 的一个解。一般来说，我们一般将 \(n\) 次单位根直接代指 \(\omega_n\)，即从 \(1\) 开始逆时针方向的第一个单位根。

下面我们讨论一下单位根的一些性质，它是我们实现 FFT 的关键：

循环性：由 \(\omega_n^n =1\) 可知，\(\omega_n^k\) 的循环节是 \(n\)，这也就是你在复平面上一次转 \(\frac{2\pi}{n}\) 弧度，转 \(n\) 次就会回到原点。所以说，\(\omega_n^k = \omega_n^{k+tn}(t\in \mathbb{Z})\)。
\(\omega_n^k = \omega_{cn}^{ck}(c > 0)\)，这个放到复平面上更容易理解，你把整个圆分成 \(cn\) 份，它的第 \(ck\) 个单位根就是你把圆分成 \(n\) 份，它的第 \(k\) 个单位根。
当 \(n\) 为偶数时，将 \(\omega_n^k\) 取反相当于将其逆时针（或顺时针）转半圈，所以 \(\omega_n^k = -\omega_n^{k\pm\frac{n}{2}}(2\mid n)\)。
单位根的对称性：因为 \(n\) 次单位根将单位圆 \(n\) 等分，均匀分布在圆周，所以它们的中心就在原点，即 \(\displaystyle \sum_{i=0}^{n-1}\omega_n^i = 0\)。
若 \(\gcd(k,n) = 1\)，则 \(\omega_n^k\) 称为本原单位根。所有本原单位根的 \(0\sim n-1\) 次幂互不相同，你会发现，它似乎和原根有着极大的相似性。

单位根与原根

阐释了单位根的性质以后，我们发现，单位根和原根之间似乎有着奇妙的关联，可以说，原根就是模 \(p\) 意义下整数域的单位根。

设 \(n=\varphi(p)\) 且 \(p\) 存在原根 \(g\)，则 \(g^0,g^1,\dots,g^{n-1},g^n = g^0,g^{n+1}=g^1\) 这样的循环和 \(n\) 次单位根的循环一模一样。这使得在模 \(p\) 意义下涉及 \(n\) 次单位根的运算时，可直接用原根 \(g\) 代替。也就是说，对于 \(d\mid n,g^{\frac{n}{d}}\) 可以直接代替模 \(p\) 意义下的 \(d\) 次单位根。

结合群论来看，单位根和原根都是对应域上一个大小为 \(n=\varphi(p)\) 的循环群的生成元，它们均满足 \(n\) 次幂时对应域的单位元，且它们的 \(0\sim n-1\) 次幂互不相同。换言之，它们同构。　

这就是快速傅里叶变换 FFT 和快速数论变化 NTT 之间的内在联系。

欧拉公式

欧拉公式的内容：

\[e^{ix} = \cos x + i\sin x \]

即单位圆上从 \((1,0)\) 开始旋转 \(x\) 弧度得到的复数，也即大小为 \(x\) 弧度的角的终边与单位圆的交点。

有了这个公式，我们可以更简介的描述一个复数：\(re^{i\theta}\) 表示一个模长为 \(r\)，辐角为 \(\theta\) 的复数，使记号变得更简洁。

将该表示法应用于单位根，可得 \(\omega_n=e^{\frac{2\pi}{n}i}\)。

代入 \(t=\pi\)，得到著名等式

\[e^{i\pi} = -1 \]

代入 \(t = 2\pi = \tau\)，得

\[e^{i\tau} = 1 \]

这说明对于任意 \(k\in\mathbb{Z},(e^{2\pi i})^{k+\frac{t}{n}}\) 相等恰对应 \(\omega_n^{kn+t}\) 相等。

多项式

基本概念

形如 \(\displaystyle \sum_{i=0}^n a_ix^i\) 的有限和式称为多项式。记作 \(\displaystyle f(x)= \sum_{i=0}^na_ix^i\)。

其中，\(a_i\) 称为 \(i\) 次项前的系数，也称 \(x^i\) 前的系数，记作 \([x^i]f(x)\)。超过最高次数 \(n\) 的系数 \(a_i(i>n)\) 视为 \(0\)。

当项数无限时，形如 \(\displaystyle \sum_{i=0}^{\infty}a_ix^i\) 的和式，称为形式幂级数，它在生成函数的部分出现过，在这里我们不予讨论。

多项式系数非零的最高次项的次数称为该多项式的度，或者叫次数，记作 \(\deg f\)。
使得 \(f(x) = 0\) 的所有 \(x\) 称为多项式的根。
若 \(a_i\) 均为实数，则称 \(f\) 为实系数多项式。若 \(a_i\) 可以均为复数，则称 \(f\) 为复系数多项式。
代数基本定理：任何非零一元 \(n\) 次复系数多项式恰有 \(n\) 个复数根。这些复数根可能重合。证明？略/cy。

系数表示法和点值表示法

\(\displaystyle f(x)=\sum_{i=0}^na_ix^i\) 这样的式子给出了所有 \(i\) 次项前的系数，这种描述多项式的方法称为系数表示法，这也是我们最常见的表示方法。

将 \(x=x_i\) 代入，得到 \(y_i=f(x_i)\)，称 \((x_i,y_i)\) 为 \(f\) 在 \(x_i\) 处的点值。用若干点值 \((x_i,y_i)\) 描述多项式的方法称为点值表示法。

我们可以探究一下，给出 \(n\) 个 \(x_i\) 互不相同的点值 \((x_0,y_0),\dots,(x_{n-1},y_{n-1})\)，它所唯一确定的多项式的最高次数。

由两点确定一条直线入手，我们猜测是 \(n-1\)，事实上，的确如此。因为 \(n-1\) 次多项式需要 \(n\) 个系数描述，而 \(n\) 个点值恰好就能提供 \(n\) 个信息。

证明就考虑我们把点值代入到 \(n-1\) 次多项式中，得到 \(n\) 元线性方程组，我们把它代入以后，该线性方程组的系数矩阵就是一个 \(n\) 行 \(n\) 列的范德蒙德矩阵，因为 \(x_i\) 互不相同，所以行列式非零，方程组的解唯一。

所以我们得到一个结论：\(n\) 个点值唯一确定的多项式的最高次数为 \(n-1\)。

从系数表示法转为点值表示法称为求值。
从点值表示法转为系数表示法称为插值。

多项式的运算

多项式运算

设 \(\displaystyle f(x)=\sum_{i=0}^na_ix^i,g(x) = \sum_{i=0}^mb_ix^i\)

系数表示法

设 \(h = f+g\)，则

\[h(x)=f(x)+g(x)=\sum_{i=0}^{\max(n,m)}(a_i+b_i)x^i \]

也就是两多项式相加，对应系数相加，且 \(\deg (f+g) = \max(\deg f,\deg g)\)。

设 \(h = f * g\)，则

\[h(x)=f(x)g(x) = \sum_{i=0}^{n+m}(\sum_{j=0}^ia_jb_{i-j})x^i \]

也就是两多项式相乘，每两个系数相乘贡献至次数之和的系数，\(\deg(f * g) = \deg f + \deg g\)。

可以看出在系数表示法下，多项式相加的复杂度为 \(O(\max(n,m))\)，多项式相乘的复杂度为 \(O(nm)\)。

点值表示法

根据 \((f+g)(x) = f(x)+g(x)\)，可知两个多项式相加时，对应点值相加。
根据 \((fg)(x) = f(x)g(x)\)，可知两个多项式相乘时，对应点值相乘。

因此，在点值表示法下，计算两个多项式相加需要 \(\max(n,m)+1\) 个点值，计算两个多项式相乘也需要同样多的点值，复杂度均为 \(O(n+m)\)

注：我们常用 \(f * g\) 和 \(fg\) 表示多项式相乘，即进行加法卷积；用 \(f \cdot g\) 表示多项式点乘，即对应系数相乘。

实际上，FFT 等快速多项式乘法就是运用的这个性质来快速相乘。先转化成点值表示法，相乘后在转回系数表示法，时间复杂度 \(\mathcal{O}((n+m)\log(n+m))\)，我们在后面部分会讲述这个算法。

拉格朗日插值

刚才我们得到一个结论：\(n\) 个点值唯一确定的多项式的最高次数为 \(n-1\)。接下来我们思考如何在点值表示法和系数表示法之间转化。

从系数表示法转为点值表示法，最简单也是最常见的是 \(O(n^2)\) 直接代入 \(n\) 个点每次 \(O(n)\) 求值。\(O(n\log^2n)\) 的多项式多点求值是高级科技，以后我学了会补充上，现在先不讨论。

从点值表示法转为系数表示法，首先因为可以先设出系数表示法的形式，然后把 \(x_i\) 代入进去，这就变成了 \(n\) 个 \(n\) 元一次方程组的形式，显然通过高斯消元就可以 \(O(n^3)\) 的求解此问题了。

还有一种方法，就是我们现在要提到的拉格朗日插值法，它能在 \(O(n^2)\) 的时间复杂度内求解此问题。

算法内容

拉格朗日插值的构造方法其实和中国剩余定理的构造方式有着异曲同工之处。

简单来说，就是我们需要构造一个 \(n\) 次多项式，使得它满足在已知的点 \(x_i\) 处取值为 \(y_i\)。

构造 \(f_i(x)\)，使得其仅在 \(x_i\) 处取值为 \(1\)，其他 \(x_j,j\not= i\) 处取值为 \(0\)。

那么也就是说 \(y_if_i(x)\)，仅在 \(x_i\) 处取值为 \(y_i\)，其他 \(x_j,j\not= i\) 处取值为 \(0\)。

接下来我们考虑如何构造 \(f_i(x)\)：

如果要在 \(x_j,j\not=i\) 处取值为 \(0\)，可以让 \((x-x_j),j\not=i\) 乘起来，即 \(\displaystyle \prod_{j\not=i}(x-x_j)\)，我们把它记为 \(g(x)\)。有了这个式子，对于不是 \(x_i\) 的地方，取值就都是 \(0\) 了。
如果要在 \(x_i\) 处取值为 \(1\)，那么就让 \(f_i(x) = \frac{g(x)}{g(x_i)}\)，这样当 \(x=x_i\) 时，\(f_i(x)\) 的取值就为 \(1\) 了，因为当 \(i\not=j\) 时，\(x_i\not=x_j\)，所以不会出现除以 \(0\) 的情况。

综上，采取一个类似于 CRT 的构造方法，我们就构造出了唯一的符合要求的 \(n\) 次多项式：

\[\sum_{i=1}^ny_i\prod_{j\not=i}\frac{x-x_j}{x_i-x_j} \]

为得到 \(f\) 的各项系数，我们先 \(O(n^2)\) 的算出 \(\displaystyle F(x) = \prod_{i=0}^{n-1}(x-x_i)\)，对每个 \(i\) 暴力 \(O(n)\) 的除掉一次式 \((x-x_i)\)，算出 \(\frac{F(x)}{x-x_i}\) 的各项系数。这一步的目的就是求分式上面那一部分，然后我们要做的就是在乘以 \(\frac{y_i}{\prod_{j\not=i}x_i-x_j}\) 得到 \(f_i\)，这个分式的下面我们可以 \(O(n^2)\) 预处理出来，最后的答案就是 \(\displaystyle f = \sum_{i=0}^{n-1}f_i\)，最后的时间复杂度就是 \(O(n^2)\)。

通常情况下，以模板题为例，它会让你求出 \(f(x)\) 在给定某个 \(x\) 处的取值，此时我们不把 \(x\) 看成一个未知量，而是直接代入 \(x\)，时间复杂度仍为 \(O(n^2)\)。

signed main()
{
	n = read() , k = read();
	for(re int i=1;i<=n;i++) x[i] = read() , y[i] = read();
	for(re int i=1;i<=n;i++)
	{
		nume = deno = 1;
		for(re int j=1;j<=n;j++)
		{
			if(i == j) continue;
			nume = nume * ((k - x[j] + mod) % mod) % mod;
			deno = deno * ((x[i] - x[j] + mod) % mod) % mod;
		}
		ans = (ans + y[i] * nume % mod * ksm(deno,mod-2) % mod) % mod;
	}
	cout << ans;
	return 0;
}

多项式快速插值在 \(O(n\log^2n)\) 的时间内将点值表示法转化为系数表示法，这个也是以后再讨论。

连续取值插值

对于给定点值横坐标为连续整数时，我们有 \(O(n)\) 插值的方法。

以 \(0\sim n-1\) ，即 \(x_i =i\) 为例：

\[f(x)=\sum_{i=0}^{n-1}y_i\prod_{j\not=i}\frac{x-j}{i-j} \]

分子是 \(\prod(x-i)\) 少了一项 \((x-i)\)，我们同时维护一个前缀后缀积即可。设 \(\displaystyle p_i = \prod_{j=0}^{i-1}(x-j),s_i = \prod_{j=i+1}^{n-1}(x-j)\)
分母对于 \(\displaystyle i>j,\prod_{j=0}^{i-1}(i-j) =i!\)；对于 \(\displaystyle i<j,\prod_{j=i+1}^{n-1}(i-j) =(-1)(-2)\dots(i-n+1)\)，将所有负号提出来，得到 \((-1)^{n-i-1}(n-i-1)!\)，因此，最终结果就是

\[f(x) = \sum_{i=0}^{n-1}y_i\frac{p_is_i}{(-1)^{n-i-1}i!(n-i-1)!} \]

预处理阶乘逆元，时间复杂度 \(O(n)\)。

标签：frac,多项式,单位根,表示法,复数,相关,theta
From： https://www.cnblogs.com/bloodstalk/p/17496815.html

多项式相关