打个广告QwQ
对应的FFT洛谷blog链接
对应的csdn博客链接
个人觉得洛谷的观感最好。
不忘历史
八百年前学了 \(\text{FFT}\),因vicky过于垃圾,遂放弃。
七百年前重拾 \(\text{FFT}\),勉强搞懂了它的递归写法,因vicky再一次懒癌附体,遂连板题都没写就弃疗了。
历史的今天 (是今天才怪),vicky重学了 \(\text{FFT}\)但仍然没写板题。
今天的昨天,vicky和蔼的教练给她讲了 \(\text{FWT}\),vicky当然是继续弃疗。
于是vicky决定复习一下 \(\text{FFT}\)。
这时报应来了,vicky发现她的FFT学得很杂。(就vicky这有兴致就看看没兴致就不学了的学法她学得不杂才怪
于是vicky开了这个坑但是选择继续摆烂。
让我们采访一下vicky: QwQ
-
Q:请问您什么时候更完?
-
A:vicky:别指望我更完了,关于vicky,她死了。
有些不得不说在前面的话
因为这些都是我边口胡边学的,其中一部分内容甚至是我在晚上睡前冥想的时候脑子里面突然冒出来、第二天上竞赛课时加以草率的验证才得到的。
所以这篇blog难免会出现很多很多的锅,各位发现了我在一些内容上理解/描述有误的话请私信or直接在评论区下面给我指出来,真的很感谢www \(\text{QwQ}\)。
因为这篇文章主要是让我用来复习 \(\text{FFT\&NTT\&FWT}\) 用的,所以一些我觉得无关紧要的概念名词在这篇blog中有一定概率不会被我说起。(即提到相关概念时我也不一定会专门告诉你这个概念的专有名词叫啥)
\(\text{Reference meterial}\)
-
小学生都能看懂的FFT!!!——\(\text{Written by }\)胡小兔
-
教练PPT(不知道教练给不给放所以不放了)
\(\text{O(n log}_2\text{n)}\) 的多项式乘法:\(\text{FFT}\)
\(\text{Part 0.}\) 点值表示&系数表示
\(\text{0.1}\) 点值表示
-
对于次数为 \(n\) 的多项式,我们很容易发现,只要我们代入 \(n+1\) 个不同的 \(x\) 值求得 \(n+1\) 个函数值,这 \(n+1\) 个函数值完全可以代替原来多项式的系数表示,让我们能够通过拉格朗日插值法 \(O(n)\) 求出任意一个函数值。
-
也就是说想要通过函数值表示一个次数为 \(n\) 的多项式我们只需要 \(n+1\) 个 \(x\) 的取值不同的函数值就可以表示出这个多项式。
-
此时我们用 \(n+1\) 个点值表示一个次数为 \(n\) 的多项式,故称其为点值表示。
PS:拉插不是 \(FFT\) 的重点,所以这里为了日后vicky复习 \(FFT\) 时不犯迷糊着想,就不对拉插进行过多阐述。想学的话自己搜blog吧,这玩意还是蛮好学的。
\(\text{0.2}\) 系数表示
我写由题意得应该不会被骂吧。- 具体例子就是: \(A(x)=a_0+a_1x+x_2x^2+\cdots+a_nx^n\),这就是系数表示。
\(\text{Part 1.FFT}\) 思路概述
现在我们有三个多项式:
\(A(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1},B(x)=b_0+\cdots+b_{n-1}x^{n-1}\)。
\(C(x)=A(x)*B(x)=\sum\limits_{i=0}^{2n-2}c_ix^i\) 。
对于多项式 \(C(x)=A(x)*B(x)\) 而言,我们如果用点值表示这个多项式,因为它的次数为 \(2n-2\) ,所以我们只需要求出 \(2n-1\) 个 \(C(x)\) 的函数值,就可以在 \(O(n)\) 的时间复杂度内求出多项式 \(A(x)\) 和 \(B(x)\) 的乘积。
那么此时求两个多项式相乘的思路其实就很明确了:
- 将多项式 \(A(x)\) 和 \(B(x)\) 由系数表示转化为点值表示,然后然后将它们俩相乘。【每求解一个 \(C(x)\) 所需要的时间均为 \(O(n)\) ,\(C(x)\) 若要使用点值表示则需要求 \(2n+1\) 个 \(C(x)\) 的点值,所以这里如果使用朴素算法转化点值表示的话时间复杂度就是 \(O(n^2)\) 】
- 将 \(C(x)\) 的点值表示转化为系数表示,然后我们就可以非常自然地求得任意 \(C(x)\) 了。(这里用拉插的话时间复杂度又是 \(O(n^2)\) )
- 那么, \(FFT\) 要做的其实就是用一些神奇技巧来将两个转化过程简化。
\(\text{Part 2.}\) 关于复数
这里坚持住的话后面的 \(FFT\) 理解起来其实就很简单了。
首先我们了解一些概念。
对于一个复数 \(a+bi\),我们有两种理解方式:(因为这些都是vicky边口胡边自学的,所以有错记得跟我说一声
- 一个起点为原点的向量。
- 平面直角坐标系上的点 \((a,b)\)。
两个复数相乘的规则如下:模长相乘,幅角相加。
模长就是点 \((a,b)\) 到原点的距离,这里也可以理解为向量的模长。幅角为该复数所对应的向量与 \(x\) 轴的逆时针夹角。
如下图:
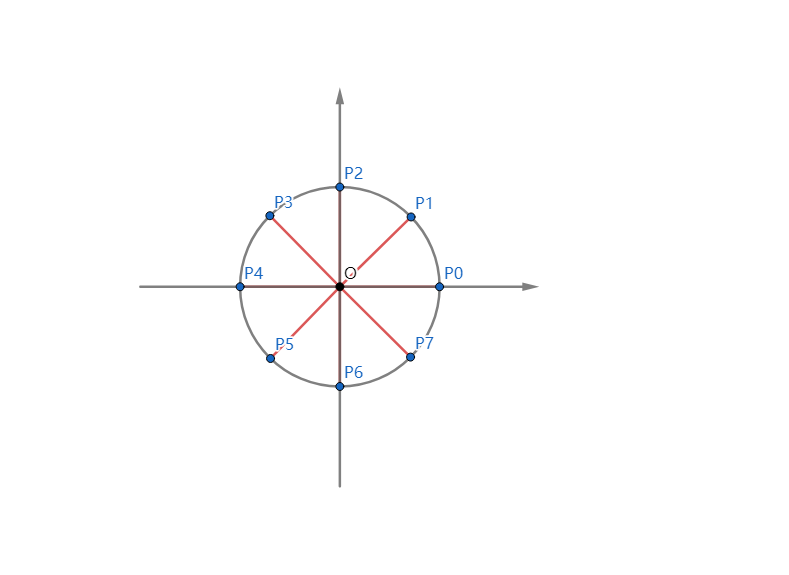
图中 \(P_6\) 的幅角为 \(270\) 度,\((P_3)^2=P_6\)。
幅角相加的概念要理解到位。
介绍了基本虚数的概念之后,我们此时再引入一个新的概念:\(\omega _n^i\)。
我们以原点为圆心作一个圆,取该圆与 \(x\) 轴正半轴的交点所表示的那个复数作为第一个点,我们将其命名为 \(\omega_n^0\) 。
我们将这个圆平均分为 \(n\) 份,每一份都代表着一个在圆上的复数,即 \(\omega_n^i\) ,我们将复数 \(\omega_n^0\) 看作一个向量,对它进行若干次旋转,每次旋转都转 \(\frac{360}{n}\)度,那么当我们进行了 \(i\) 次旋转之后我们就会得到新的复数 \(\omega_n^{i\%n}\) ,其幅角为 \(\frac{360}{n}\cdot i\) 度。
如上图,\(P_0\) 为 \(\omega_8^0\) ,\(P_5\) 为 \(\omega_8^5\) ,即 \(\omega_8^0\) 经过 \(5\) 次旋转之后得到的幅角为 \(\frac{360}{8}*5=225\) 度的复数。
总结一下,\(\omega_n^i\) 的意义即为:
- 将一个以原点为圆心的圆等分为 \(n\) 份,每一份对应圆上的一个代表复数的点。
- 定义该圆与x轴正半轴的交点为 \(\omega_n^0\)。
- 该复数的幅角度数为 \(\frac{360}{n}\cdot i\) 度,也可以理解为它在 \(\omega_n^0\) 幅角的基础上加了 \(i\) 份度数为 \(\frac{360}{n}\) 度的幅角(即 \(\omega_n^0\) 等角度地旋转 \(i\) 次得到 \(\omega_n^i\) )。
且根据复数相乘幅角相加的规则以及 \(\omega_n^i\) 的定义,我们很容易得到不同复数间的一些关系:
-
\(\omega_n^{2i}=(\omega_n^i)^2=\omega_{\frac{n}{2}}^i\)
-
\(\omega_n^i=\omega_n^{i\%n}\)
-
\(\omega_n^{i+\frac{n}{2}}=-\omega_n^i\)
垃圾markdown逼我用三级标题是吧。
其中最后一条关系还牵及到一个概念:共轭复数。
我们称\(\omega_n^{i+\frac{n}{2}}\) 和 \(-\omega_n^i\) 互为共轭复数。正式一点地描述,即实部相等,虚部互为相反数的两复数互为共轭复数。从几何意义上来说,两个共轭复数所对应的向量是共线的。(其实共不共线什么的也不重要就是了
上面的两个式子直接套 \(\omega_n^i\) 上下标的定义就可以很容易证得了吧。QwQ
离散傅里叶变换
我知道你很慌但你先别慌。
离散傅里叶变换其实只是一个概念而已,没啥难理解的地方。
上面说过了,对于一个次数为 \(n\) 的多项式 \(f(x)\) ,若我们要对其用点值表示,则需要取 \(n+1\) 个不同的 \(x\) 值代入得到 \(n+1\) 个函数值来表示这个函数 \(f(x)\) 。
那么这 \(n+1\) 个不同的 \(x\) 值我们为何不去取 \((\omega_{n+1}^0,\cdots,\omega_{n+1}^{n+1})\) 上的值呢?
因为正经人谁会想到这种奇怪的取法啊喂! QAQ
离散傅里叶变换的定义其实就是对于一个次数为 \(n\) 的函数 \(f(x)\) ,我们取函数 \(f(x)\) 在 \((\omega_{n+1}^0,\cdots,\omega_{n+1}^{n+1})\) 上的取值作为点值表示。
简而论之,一个函数在 \(n+1\) 个特殊位置上取值并将其作为该函数的点值表示,这个点值表示就是离散傅里叶变换。
再说一遍!一个函数的离散傅里叶变换是该函数的点值表示而不是单独一个点值!(写给我自己看的,没有任何侮辱各位智商的意思在。
\(\text{Part 3.}\) 复数在 \(\text{FFT}\) 的两个变换过程中的运用
搞定了复数!我们其实离搞懂 \(\text{FFT}\) 就差推几个式子的功夫啦!QwQ
下面的式子推导对我这样的数学弱智来说都还是很友好的,所以说其他人完全不用怕搞不懂 \(\text{FFT}\) 的式子推导就是了。
实在推不出来你把结论记下来感觉其实也没啥问题。
\(\text{Part 3.0}\) 回顾
咱们先回顾一下 \(\text{FFT}\) 的两个转化过程:
- 系数表示 -> 点值表示。(具体来说是利用多项式 \(A(x)\) 和 \(B(x)\) 的系数表示求得 \(C(x)\) 的点值表示。)
- 点值表示 -> 系数表示。(将 \(C(x)\) 的点值表示转化为系数表示。)
\(\text{Part 3.1}\) 系数表示 -> 点值表示
我们现有多项式 \(C(x)=A(x)*B(x)=c_0+\cdots+c_{2n-2}\cdot x^{2n-2}\)。
现在我们再弄两个多项式出来:
\[C_1(x)=c_0+c_2\cdot x+\cdots+c_{2n-2}\cdot x^{n-1} \]\[C_2(x)=c_1+c_3\cdot x+\cdots+c_{2n-1}\cdot x^{n-1} \]此时我们就可以将 \(C(x)\) 表示如下:
\[C(x)=C_1(x^2)+x\cdot C_2(x^2) \]那么若我们将 \(C(x)\) 的系数表示转化为 \(C(x)\) 对应的离散傅里叶变换。
即系数表示 -> 点值表示。
为了下面的式子推导看上去更简洁,我们将 \(C(x)\) 的次数设为 \(n-1\) ,即函数 \(C(x)\) 的离散傅里叶变换在 \((\omega_n^0,\cdots,\omega_n^n)\) 处取值。(不然满屏的 \(\omega_{2n-1}^i\)谁受得了啊喂!QAQ
那么对于任意 \(C(x)\) 在 \(\omega_n^i\) 处的点值求值,我们可以将点值求值过程分类讨论后进行转化:
温馨提示: \(\omega_n^0=\omega_n^n=1,\omega_n^\frac{n}{2}=-1\)
- \(0\leq i<\frac{n}{2}\):
- \(\frac{n}{2}\leq i\leq n\),设 \(i=k+\frac{n}{2}(0\leq k\leq \frac{n}{2})\) :
我们对比一下两种情况下 \(C(\omega_n^i)\) 最终化出来的式子:
- \(C(\omega_n^i)=C_1(\omega_\frac{n}{2}^{i})+\omega_n^i\cdot C_2(\omega_\frac{n}{2}^{i})\)
- \(C(\omega_n^i)=C_1(\omega_{\frac{n}{2}}^{k})- \omega_n^{k}\cdot C_2(\omega_{\frac{n}{2}}^{k})\)
发现没有,我们通过式子推导,使得我们只需要求函数 \(C_1,,C_2\) 在 \((\omega_{\frac{n}{2}}^0,\cdots,\omega_{\frac{n}{2}}^{\frac{n}{2}-1})\)处的取值就可以求得函数 \(C\) 的点值了。
现在问题就变得很简单了,我们只需递推实现即可,碰到递归边界 \(n=1\) 时我们直接套 \(C(\omega_n^i)=A(\omega_n^i)*B(\omega_n^i)\) 求值返回即可。
现在我们看回时间复杂度。
对于每一个 \(C(\omega_n^i)(0\leq i<n)\) ,如果用递归实现,递归边界为显然为 \(C(\omega_n^i)\) 中的 \(n\) 的值为 \(1\) 。
每次 \(C(\omega_n^i)\) 中的 \(n\) 都会缩小一半,不难得到我们要进行 \(log_2n\) 次递归,即每次求 \(C(\omega_n^i)\) 的点值的时间复杂度为,我们一共要求的点值总数与 \(n\) 成正比,所以求 \(C(x)\) 的点值表示所需的时间复杂度为 \(\text{O(n log n)}\) 。
但是,我们不能忽视的是,\(\text{O(nlog}_2\text{n)}\) 仅仅只是递归实现 \(\text{FFT}\) 的渐进时间复杂度而已,也就是说,递归实现的 \(\text{FFT}\) 在某些凉心畜题人的数据下还是很容易被卡成 \(TLE\) 的。
事实上我们有更快的非递归 \(\text{FFT}\) 实现方式,且vicky个人认为非递归版本并不比递归版本难写多少。
都学到这里了不把 \(\text{FFT}\) 的优化学完不就前功尽弃了嘛!QAQ
但是为了日后vicky看这篇帖子不会被冲昏头脑,所以我们先把 \(\text{FFT}\) 的基本思想讲完再进一步对 \(\text{FFT}\) 的代码实现进行讲解。QwQ
\(\text{Part 3.2}\) 点值表示 -> 系数表示
这部分主要也是推式子,而且相对上一部分来说这部分的式子推导还是友好很多的。
但是上一部分的其实也不难,直接套 \(\omega\) 的定义就能推出来了对吧。
说实话其实这部分直接记结论也完全没有问题的。
在上一部分中我们求的是 \(C(x)\) 在 \((\omega_n^0,\cdots,\omega_n^{n-1})\) 处取值的点值表示,也就是它的离散傅里叶变换,那么如果我们是否可以这些在点值上进行一些瞎搞去求得 \(C(x)\) 的系数表示呢?
答案是可以的。
为了下面的式子推导相对简洁,我们先将 \(C(x)\) 的离散傅里叶变换 \((C(\omega_n^0),\cdots,C(\omega_n^{n-1}))\) 分别设为数组 \((d_0,d_1,\cdots,d_{n-1})\) 。
我们将 \(C(x)\) 的离散傅里叶变换 \((d_0,\cdots,d_{n-1})\) 作为另一个次数为 \(n-1\) 的多项式 \(D(x)\) 的系数表示,即:
\[D(x)=C(\omega_n^0)+C(\omega_n^1)\cdot x+\cdots+C(\omega_n^{n-1})\cdot x^{n-1} \]\[=d_0+d_1x+\cdots+d_{n-1}x^{n-1} \]根据 \(d_i\) 的定义,显然有 \(d_i=C(\omega_n^i)=\sum\limits_{i=0}^{n-1}c_i\cdot x^i\)。
我们再将 \(D(x)\) 的离散傅里叶变换表示成 \((e_0,\cdots,e_n-1)\),但是这里需要注意的是,我们不再是在 \((\omega_n^0,\cdots,\omega_n^{n-1})\) 处取值,而是在 \((\omega_n^{0},\omega_n^{-1},\cdots,\omega_n^{1-n})\) 处进行取值,即 \(e_i=\sum\limits_{i=0}^{n-1}x^{i}\cdot \omega_n^{-i}\) 。
那么对于每一个 \(e_i\) ,我们可以尝试一下对它进行式子推导,看看能否找出一种通过 \(e_i\) 快速求出 \(c_i\) 的办法:
\[e_k=D(\omega_n^{-k})=\sum\limits_{i=0}^{n-1}d_i\cdot (\omega_n^{-k})^i=\sum\limits_{i=0}^{n-1}D(\omega_n^{i})\cdot (\omega_n^{-k})^i \]\[=\sum\limits_{i=0}^{n-1}\left(\sum\limits_{j=0}^{n-1}c_j\cdot (\omega_n^i)^j\right)\cdot (\omega_n^{-k})^i \]\[=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}c_j\cdot (\omega_n^i)^j\cdot (\omega_n^{-k})^i=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}c_j\cdot \omega_n^{i\cdot j}\cdot \omega_n^{-k\cdot i} \]\[=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}c_j\cdot \omega_n^{i\cdot (j-k)}==\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}c_j\cdot (\omega_n^{j-k})^i \]\[=\sum\limits_{j=0}^{n-1}c_j\cdot \sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i \]\(k\) 显然可以理解成一个定值,我们枚举到每一个 \(j\) 的时候,\(j\) 其实也算作是一个定值,此时不难发现 \(\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i\) 其实就是个等比数列求和。
因为 \(j\) 的值是在 \([0,n-1]\) 范围内进行枚举的,因此我们可以对 \(j-k\) 进行分类讨论,然后再求 \(\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i\) 的值:
- \(j-k=0\),即 \(j=k\) :
此时显然有:
\[\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i=\sum\limits_{i=0}^{n-1}(\omega_n^0)^i=\sum\limits_{i=0}^{n-1}1^i=n \]- \(j-k\neq 0\):
根据等比数列求和公式 \(sum=\dfrac{a_1\cdot (1-q^n)}{1-q}\) ,我们易得:
PS:公式中的 \(a_1\) 为数列首项,\(q\) 为公比,\(n\) 为项数。
为了下面的式子推导看起来更简洁一些,我们设 \(W=j-k\) 。
注意,下面式子中的 \(j\) 与 \(k\) 我们均看作定值。(不知道为啥的应该好好反思一下自己到底看没看懂上面的内容了……QwQ
也就是说,当且仅当 \(\sum\limits_{j=0}^{n-1}\) 枚举到 \(k\) 时,\(\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i\) 才会有值,且此时\(\sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i\) 的值为 \(n\)。
那么我们就可以进一步转化 \(e_k\) :
\[e_k=\sum\limits_{j=0}^{n-1}c_j\cdot \sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i \]我们按上面分类讨论的两种情况进行求值:
\[e_k=\left(\sum\limits_{j=0,j\neq k}^{n-1}c_j \cdot \sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i\right)+c_k\cdot \sum\limits_{i=0}^{n-1}(\omega_n^{j-k})^i \]\[=\left(\sum\limits_{j=0,j\neq k}^{n-1}c_j \cdot 0\right)+c_k\cdot n \]\[=c_k\cdot n \]这个时候要怎么求 \(c_k\) 就不用我说了吧。 QwQ
\[c_k=\dfrac{e_k}{n} \]此时我们运用上一部分中的系数表示->点值表示的方法即可在 \(\text{O(log}_2\text{n)}\) 的时间复杂度下求每个 \(e_k\) 也就是 \(D(\omega_n^{-k})\) 的值,每求出一个 \(e_k\) ,我们就可以运用 \(c_k=\dfrac{e_k}{n}\) 这一关系 \(\text{O(1)}\) 求出 \(C(x)\) 的第 \(k\) 项系数。
而 \(C(x)\) 的项数与 \(n\) 成正比,所以我们运用这一方法实现点值表示->系数表示的渐进时间复杂度即为 \(\text{O(nlog}_2\text{n)}\)。