飞机的三自由度方程
目录参考
python实现飞行控制仿真(二)——三自由度仿真_python 飞行仿真_风雨潇潇一书生的博客-CSDN博客
运动学和动力学方程
1 地面惯性坐标系下的三维空间运动学方程
[基于深度强化学习的无人机对战战术决策的研究 ](D:\CNKI E-Study\18761606609\Literature\TempRead\基于深度强化学习的无人机对战战术决策的研究_胡真财.caj)
将无人机简化为三维空间内的一个质点,为了将研究重点聚焦于格斗决策方法上的研究,本文对无人机的飞行模型设计做出如下四点假设: (1)无人机在飞行过程中不考虑空气阻力,也不考虑空气的流速,也就是说无人机的速度仅仅由自身的机动动作决定。
(2)无人机在飞行过程中没有侧滑,即侧滑角恒等于0。
(3)无人机的质量为恒定值,重力加速度,空气密度等因素不随飞行环境的变化而变化。
(4)地面参考系始终处于静止状态,忽略地球的自转对于建模的影响。 基于以上的设定,定义出无人机在地面惯性坐标系下的三维空间运动学方程如下:
\[\begin{aligned} & \frac{d x}{d t}=v \cos \theta \cos \psi \\ & \frac{d y}{d t}=v \cos \theta \sin \psi \\ & \frac{d z}{d t}=v \sin \theta \\ & \frac{d v}{d t}=g\left(N_x-\sin \theta\right) \\ & \frac{d \theta}{d t}=\frac{g}{v}\left(N_z \cos \varphi-\cos \theta\right) \\ & \frac{d \psi}{d t}=\frac{g N_z \sin \varphi}{v \cos \theta} \\ \end{aligned} \]方程组中的每一项分别表示 UCAV 三维空间坐标值、飞行速率、航向角和轨迹角的一阶微分方程, 决定了格斗过程中飞行器状态更新计算的 方法。
另一种表示,只是符号变了,上式子中的\(\theta\)为下面的\(\gamma\) , \(\varphi\)为\(mu\),
\(N_x\) 为飞行器的切向过载,表示的是飞行器在前进速度方向上受到的推力和自身重力的比值,切向过载可以改变飞行器的速度大小, \(N_x\) 可以实现飞行器加速、减速、或者匀速率飞行的控制;
\(N_z\) 是飞行器的法相过载, 表示飞行 器受到的与其机身平面垂直且方向向上的过载, 能够提供飞行器所需的升力,\(N_z\) 可以控制飞行器的俯冲, 拉起和平稳飞行的控制, 以改变飞行器的垂直高度。
\(\varphi\) 为机体的滚转角, 表示的是机体绕自身速度方向的夹角, 一般固定翼飞 滚转角实现侧身的效果, 可以为固定翼飞行器提供转弯所需要的推力 \({ }^{[48]}\), 以实现更有效的转弯。
控制量为 切向过载 \(N_x\) 法向过载\(N_z\) 滚转角 \(\varphi\)也就是图片里的\(mu\)
状态量为: 三维空间坐标值\((x,y,z)\) ,飞行速率、航迹角 、航向角
程序实现
给定初始状态
三维空间坐标值、飞行速率、航迹角 、航向角
\[x,y,z,v,\gamma,\varphi \]state = [x,y,z,v,gamma,varphi]
输入 : 控制量 切向过载 、法向过载、滚转角
\[N_x 、 N_z、 \mu \]control = [Nx , Nz , mu]
代码返回: 下一时间(一个仿真步长)的状态量
完整代码
# -*- coding: utf-8 -*-
"""
@author : zuti
@software : PyCharm
@file : 3_run_func.py
@time : 2023/3/23 19:46
@desc :
"""
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import odeint
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams.update({'font.size': 12})
# 初始姿态
init_velocity, init_gamma, init_varphi = 260., 3.14 / 10., 0.
init_x, init_y, init_z = 0., 0., 1000. # 初始位置
# todo 三个控制量
Nx = 3.0
Nz = 2.
mu = 3.14 / 12
state = [init_x, init_y, init_z, init_velocity, init_gamma, init_varphi]
control = [Nx, Nz, mu]
time = 1 # 秒 总时间
n = 10 # 仿真步数
t = np.linspace(0, time, n) # 仿真步长
def dmove2(x_input, t, control):
g = 9.81 # 重力加速度
velocity, gamma, fai = x_input
nx, nz, gunzhuan = control
velocity_ = g * (nx - np.sin(gamma)) # # 米每秒
gamma_ = (g / velocity) * (nz * np.cos(gunzhuan) - np.cos(gamma)) # 米每秒
fai_ = g * nz * np.sin(gunzhuan) / (velocity * np.cos(gamma))
return np.array([velocity_, gamma_, fai_])
def update_position(state, control, time=1, n=10):
"""
:param state: 初始状态
:param control: 控制量
:param time: 仿真时长
:param n: 仿真步数
:return:
"""
t = np.linspace(0, time, n) # 仿真步长
dt = t[1] - t[0]
state_list = np.zeros((n, 6)) # 轨迹长度
state_list[0] = state # 轨迹列表第一个元素为初始状态
x,y,z,velocity, gamma, varphi = state_list[0]
for k in range(1, n):
tspan = [t[k - 1], t[k]]
st = odeint(dmove2, (velocity, gamma, varphi), tspan, args=([control[0], control[1], control[2]],))
velocity, gamma, varphi = st[1, :]
dx = velocity * np.cos(gamma) * np.sin(varphi) * dt
dy = velocity * np.cos(gamma) * np.cos(varphi) * dt
dz = velocity * np.sin(gamma) * dt
x = x + dx
state_list[k, 0] = x
y = y + dy
state_list[k, 1] = y
z = z + dz
state_list[k, 2] = z
state_list[k, 3] = velocity
state_list[k, 4] = gamma
state_list[k, 5] = varphi
return state_list
#测试运动学方程
state_list = update_position(state,control)
print(f'轨迹 {state_list}')
#绘制图像
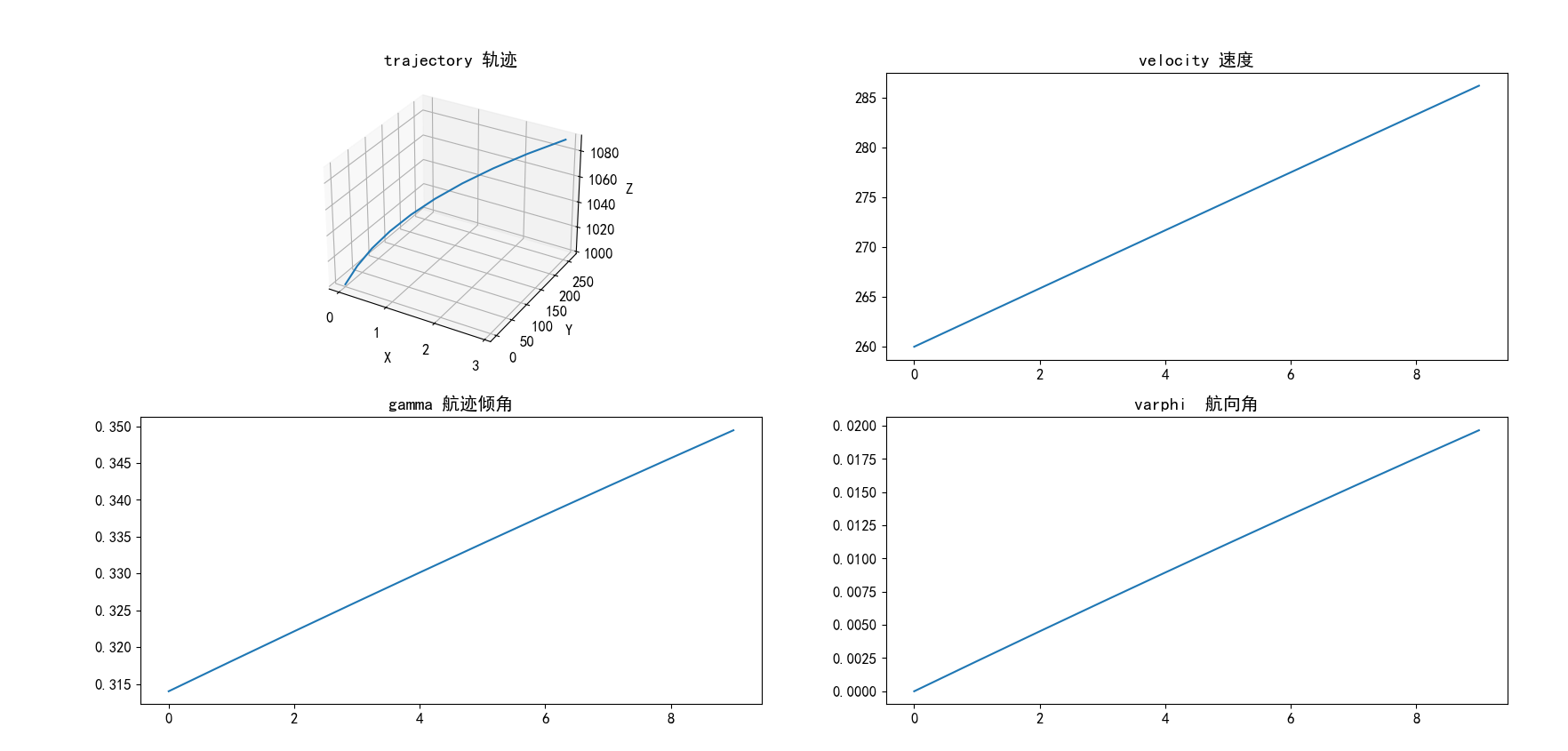
fig = plt.figure()
ax1 = fig.add_subplot(221,projection='3d')
ax1.plot(state_list[:, 0], state_list[:, 1], state_list[:, 2])
ax1.set_title('trajectory 轨迹')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')
ax2 = fig.add_subplot(222)
ax2.plot(state_list[:,3])
ax2.set_title('velocity 速度')
ax3 = fig.add_subplot(223)
ax3.plot(state_list[:,4])
ax3.set_title('gamma 航迹倾角')
ax3 = fig.add_subplot(224)
ax3.plot(state_list[:,5])
ax3.set_title('varphi 航向角')
#plt.savefig('test.jpg')
plt.show()
效果