图论系列：

前言：

僕は
明快さ故にアイロニー
優柔不断なフォローミー
後悔後悔夜の果て

相关题单：戳我

一.强连通分量相关定义

基本摘自oi wiki ，相关定义还是需要了解。(实际就是搬了个oi wiki)
强连通分量主要在研究有向图可达性，针对的图类型为有向弱联通图。

1.强连通定义

强连通：对于有向图的两点 \(u,v\)，它们互相可达。

强连通图：满足图内任意两点强连通的有向图。

强连通分量（Strongly Connected Components，SCC）：极大的强连通子图。（也就是说在同一强连通分量的任意两点都是互相可达的，于是在关心可达性时，同一强连通分量内的点等价）。

一般使用 Tarjan 求强连通分量。

2.有向图 DFS 树

对于一张有向图，对其跑 DFS ，不经过已经遍历过的点的前提下，遍历过程可以看似一颗树，称作有向图 DFS 树，单从某一点出发 DFS，不一定能访问到图上的所有结点，所以一般有向图 DFS 树是一个森林。

形成若干棵 DFS 树后，在研究强连通性时，它们之间相互独立。对于任意强连通的两点 \(u,v\) ，第一次访问它们所在的强连通分量的 DFS 树一定同时包含 \(u,v\)。

我们一般用时间戳 \(dfn_i\) 表示遍历到点 \(i\) 的时间，可以得到遍历到各个点的先后顺序。

不同于一般的树，除了树边还有其他类型的边，如图，有向图的 DFS 生成树主要有 4 种边（不一定全部出现）：

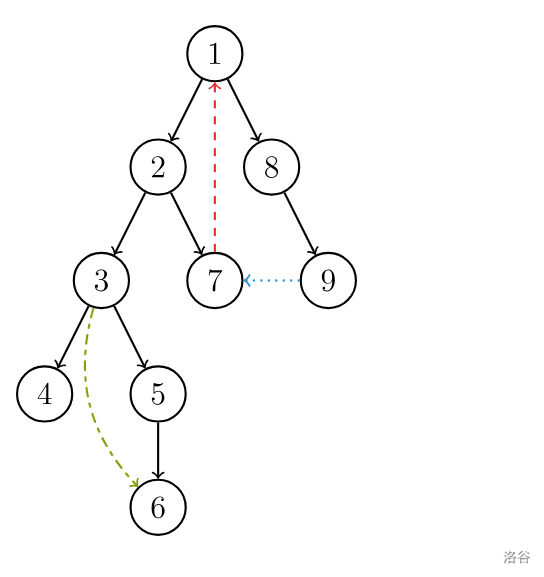
树边：就是遍历的时候经过的边，示意图中以黑色边表示，，在每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。

反祖边：示意图中以红色边表示（即 \(7 \rightarrow 1\) ），也被叫做回边，即指向祖先结点的边。

横叉边：示意图中以蓝色边表示（即 \(9 \rightarrow 7\) ），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先。

前向边：示意图中以绿色边表示（即 \(3 \rightarrow 6\) ），它是在搜索的时候遇到子树中的结点的时候形成的。

由于强连通分量主要和性有关，现在讨论各类边对可达性的影响：

对于前向边 \(u \to v\) ，\(u\) 本来通过树边就可到达 \(v\)，所以对可达性没有影响。

对于反祖边 \(v \to u\) ，\(u\) 本身可以通过树边到达 \(u \to v\) 路径上的所有点 ，而这条返祖边使得所有在 \(u \to v\) 路径上的点可以到达点 \(u\)，于是 \(u \to v\) 路径上的所有点就构成了一个强连通分量。多个返祖边结合可以形成更大更复杂的强连通结构。

对于横叉边，也可以使得时间戳减小。

通过讨论我们可以发现:

若 \(u,v\) 强连通，则 \(u,v\) 在树上路径上的所有点强连通。

强连通分量在有向图 DFS 树上弱连通。

3. Tarjan 求 SCC

Tarjan 算法基于对图进行 深度优先搜索。我们视每个连通分量为搜索树中的一棵子树，在搜索过程中，维护一个栈，每次把搜索树中尚未处理的节点加入栈中。时间复杂度是 \(O(n+m)\) 的。

在 Tarjan 算法中为每个结点 \(u\) 维护了以下几个变量：

\(dfn_u\) ：就是在 DFS 树内的时间戳。（一个结点的子树内结点的 dfn 都大于该结点的 dfn 值。）

\(low_u\) ：在 u 的子树中能够回溯到的最早的已经在栈中的结点。设以 \(u\) 为根的子树为 \(T_u\)。\(T_u\) 定义为以下结点的 \(dfn\) 的最小值：\(T_u\) 中的结点；从 \(T_u\) 通过一条不在搜索树上的边能到达的结点（要么是返祖边，要么是横叉边）。（一般初始化 \(low_u=dfn_u=++num\)）

按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索，维护每个结点的 dfn 与 low 变量，且让搜索到的结点入栈。每当找到一个强连通元素，就按照该元素包含结点数目让栈中元素出栈。在搜索过程中，对于结点 \(u\) 和与其相邻的结点 \(v\)（ \(v\) 不是 \(u\) 的父节点）考虑 3 种情况：

\(v\) 未被访问：继续对 \(v\) 进行深度搜索。在回溯过程中，用 \(low_v\) 更新 \(low_u\)。因为存在从 \(u\) 到 \(v\) 的直接路径，所以 \(v\) 能够回溯到的已经在栈中的结点，\(u\) 也一定能够回溯到。
\(v\) 被访问过，已经在栈中：根据 low 值的定义，用 \(dfn_v\) 更新 \(low_u\)。
\(v\) 被访问过，已不在栈中：说明 \(v\) 已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 \(u\) 使得 \(dfn_u=low_u\)。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 dfn 和 low 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定 \(dfn_u=low_u\) 是否成立，如果成立，则栈中 \(u\) 及其上方的结点构成一个 SCC。

一些结论：

一个点只属于一个 SCC。

SCC 缩点后，得到的新图不含环，否则环上所有结点对应的 SCC 可以形成一个更大的 SCC。这说明 SCC 缩点图是一张 DAG。

对于两个 SCC ，\(S1\) 若可达 \(S2\) 则 \(S1\) 比 \(S2\) 后弹出栈。按弹出顺序写下所有 SCC，得到缩点 DAG 的反拓扑序。因此，按编号从大到小遍历 SCC，就是按拓扑序遍历缩点 DAG。

Tarjan 缩点代码：

inline void dfs(int u)
{
	dfn[u]=low[u]=++num,vis[u]=1;//初始化，标记u在栈内
	s.push(u);//s是栈
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(!dfn[v])//子树内没有遍历过的点
		{
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v]) low[u]=min(low[u],dfn[v]);//不在子树内&没有处理过的点
	}
	if(low[u]==dfn[u])//是关键点
	{
		int x;++tot;//缩后点数+1
		while(1)
		{
			vis[(x=s.top())]=0;//出栈，已经操作，取消标记
			s.pop();
			if(x==u) break;//已经把栈内u上面的弹完了，退出
		}
	}
}