向量

定义

从偏计算机的角度分析，这是排成一列的数。

从偏物理的角度分析，这是一条有方向有长度的线段。

可以通过数形结合的方式来理解向量。

虽然向量的起点不固定，但画平面直角坐标系中的向量，我们一般将向量的起点放在 \((0, 0)\)，用向量的终点表示这个向量，如图：

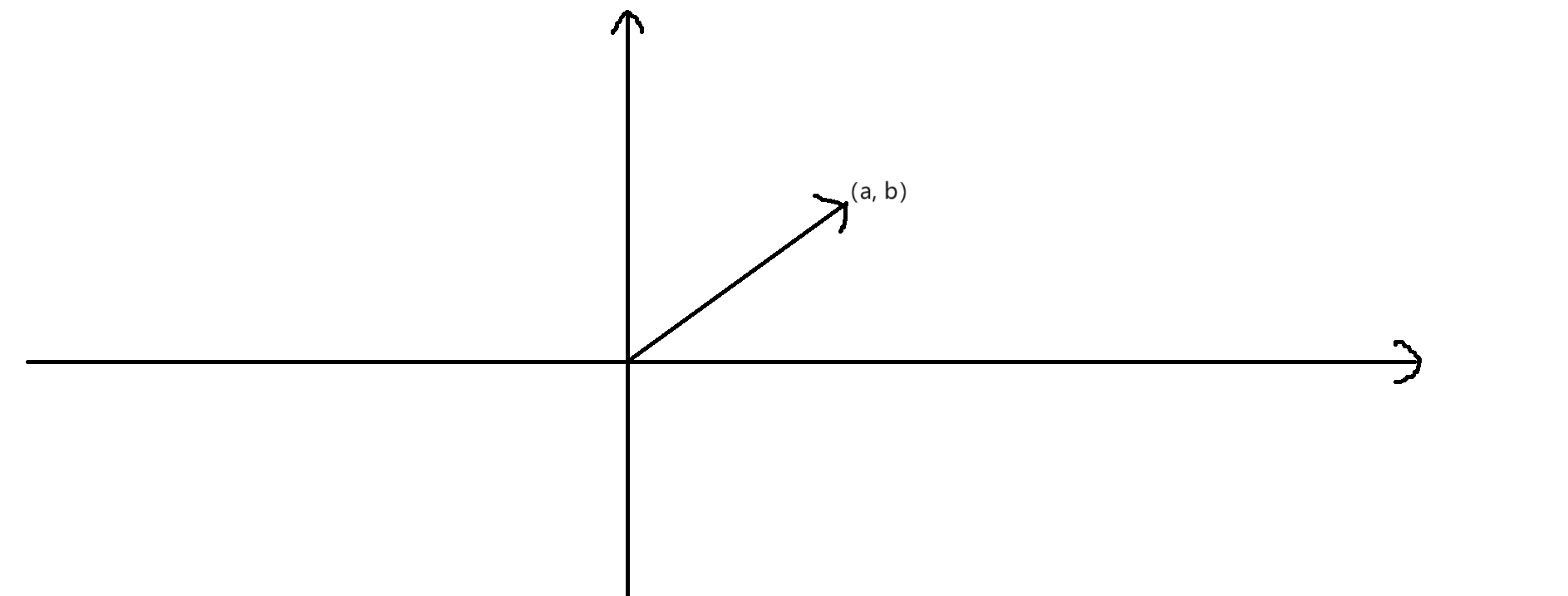
这个向量可以表示成 \((a, b)\)，用计算机的表现方式，也可以写作 \(\begin{bmatrix} a \\ b\end{bmatrix}\)

计算

详见多项式学习笔记（一）（2024.7.6）

基

其实，任何一个向量 \(\overrightarrow{v}\) 的坐标表示 \((a, b)\)，都可以表示成 \(v = a \hat{i} + b \hat{j}\)，其中 \(\hat{i}\) 和 \(\hat{j}\) 分别是 \(x\) 轴和 \(y\) 轴方向上的单位向量。

观察到，平面中的所有向量都可以表示成 \(\hat{i}\) 和 \(\hat{j}\) 的线性组合，此时 \(\hat{i}\)