CP4

反演与共轴圆系还是有很大关联的。我们说，共轴圆系反演后还是共轴圆系，理由如下：

1. 对于有两个交点的共轴圆系，反演后的所有圆还是过这两个点（的对应点），所以还是共轴圆系

2. 对于切于某点的共轴圆系，由反演的保相切，它们依旧相切与一点

3. 对于无交点的共轴圆系，我们找到与它共轭的共轴圆系（回忆共轴圆系的知识），反演后与它正交的共轴圆系还是共轴圆系，由反演的保正交，它也只能是共轴圆系

还有一个重要命题：反演圆与互为反演的两个圆共轴。若这两个圆不相交，那么它们共轴圆系的极限点互为反演

推论：若两个点关于 \(l\) 对称，反演后，两点关于 \(l'\) 为反演对应点（考虑以这两点为极限点的共轴圆系即可， \(l\) 是其中的一员，反演后依旧是）

例1

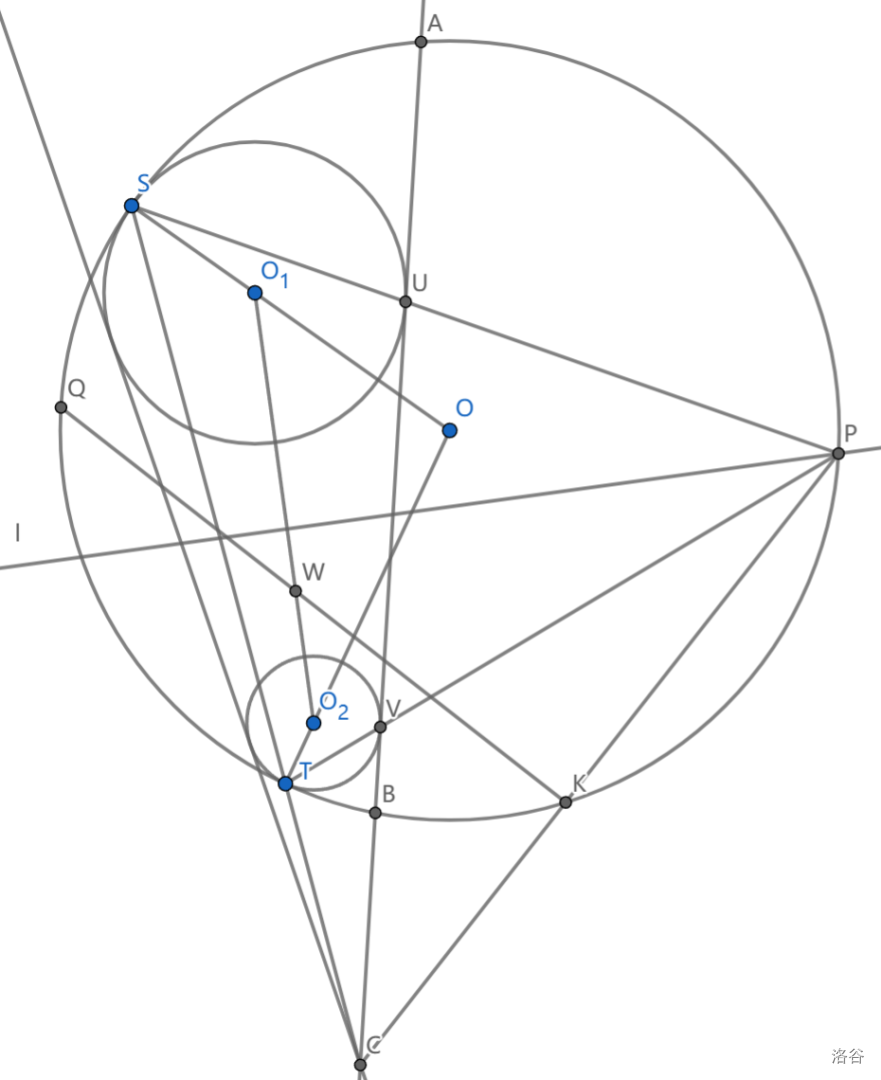
如图， \(\odot O\) 与 \(\odot O_1,\odot O_2\) 相切于点 \(S,T\) ， \(\odot O_1,\odot O_2\) 的一条外公切线交 \(\odot O\) 于 \(A,B\) ，并且两条外公切线交于点 \(C\) ， \(AB\) 的中垂线交 \(\odot O\) 于 \(P,Q\) ， \(P\) 到 \(O_1O_2\) 的距离更大，设 \(K=PC\cap \odot O\) ，求证： \(\angle QKO_1=\angle QKO_2\)

首先明确， \(STC\) 共线。梅氏定理，用 \(STC\) 割一下 \(\triangle O_1O_2O\) 就好了，没什么好说的。

看到 \(\angle CKW=Rt\angle\) 证角平分线，立马联想到阿氏圆，只要证 \((O_1,O_2;W,C)=-1,W=KQ\cap O_1O_2\) ， \(C\) 是外位似中心，那么 \(W\) 就是内位似中心

现在回顾 \(CTS\) 共线，意味着 \(CTS,CKP\) 分别是两圆的割线， \(CS\cdot CT=CK\cdot CP\) 。

这是一个很微弱的线索，如果关于 \(C\) 反演， \(S,T\) 对应，并且很大希望地， \(\odot O_1,\odot O_2\) 能够是反演对应圆

是的， \(\odot O_1,\odot O_2\) 是反演对应的。因为在此反演对应下， \(\odot O\) 不变（只是形状位置！），所以这两个圆依旧相切，切点分别是 \(S,T\) 。

我们连接 \(PS,PT\) ，由位似可以看到它们与 \(AB\) 交于 \(\odot O_1,\odot O_2\) 与 \(AB\) 的切点 \(U,V\) ，根据反演对应有 \(CU\cdot CV=CS\cdot CT\)

这意味着 \(UVTS\) 共圆，它们另一个交点 \(P\) 满足 \(PV\cdot PT=PU\cdot PS\) ， \(P\) 在两圆根轴上

我们来考虑根轴在反演后变成了什么。根轴是共轴圆系的一员，它应当还是与 \(\odot O_1,\odot O_2\) 共轴，那么它的直径在 \(CO_1O_2\) 上，并且过点 \(K\) （也就是 \(P\) 的对应点）

没错，恰好就是以 \(CW\) 为直径的圆。我们还要利用一个共轴圆的性质， \(\frac{\rho_{O_1}(C)}{\rho_{O_2}(C)}=\frac{\rho_{O_1}(W)}{\rho_{O_2}(W)}\) ，而 \(C\) 是外位似中心，说明

\(\frac{WO_1^2-r_1^2}{WO_2^2-r_2^2}=\frac{CO_1^2-r_1^2}{CO_2^2-r_2^2}=\frac{r_1^2}{r_2^2}\)

从而 \(W\) 是外位似中心，证毕。

例2

\(\triangle ABC\) 中， \(I\) 是内心，点 \(X\) 满足 \(AX+BC=BX+CA=CX+AB\) ，点 \(Y\) 满足 \(AY-BC=BY-CA=CY-AB\) ，求证： \(X,Y,I\) 共线

看到了边长有关的条件，关键的想法是，原条件等价于

\(AX-(p-a)=BX-(p-b)=CX-(p-c)=r\) ，换而言之，我们以 \(A\) 为圆心， \(p-a\) 为半径作圆（就是过内切圆切点的圆），会与以 \(X\) 为圆心， \(r\) 为半径的圆相切

同理 \(\odot Y\) 也会与这三个圆相切。一个是内切，一个是外切

现在考虑关于 \(\odot A,\odot B,\odot C\) 的根心反演，这三个圆不变。那么 \(\odot X,\odot Y\) 也还是与三个圆相切

根心 \(I\) 原来是在 \(\odot Y\) 内部的，那么反演之后，它应当在它对应圆的外部，也就是说，它变成了 \(\odot X\) ，从而两个圆心与 \(I\) 共线，证毕。

例3

圆 \(O_1,O_2,O_3\) 两两外离，圆 \(\Omega\) 与它们三个均外切，圆 \(\Gamma\) 与它们三个均内切，证明：圆 \(O_1,O_2,O_3\) 两两外位似中心构成直线是 \(\Omega,\Gamma\) 的根轴。

找到圆 \(O_1,O_2\) 的外位似中心 \(C\) ，设它们与 \(\Omega\) 的切点为 \(S_1,S_2\) ，与 \(\Gamma\) 的切点为 \(T_1,T_2\)

关于 \(C\) 反演使 \(\odot O_1\leftrightarrow \odot O_2\) 。在例1中已经提及过 \(S_1S_2C,T_1T_2C\) 共线，那么 \(S_1\leftrightarrow S_2,T_1\leftrightarrow T_2\)

即 \(CS_1\cdot CS_2=CT_1\cdot CT_2\) ， \(C\) 在根轴上，三个外位似中心都是如此，证毕。

例4

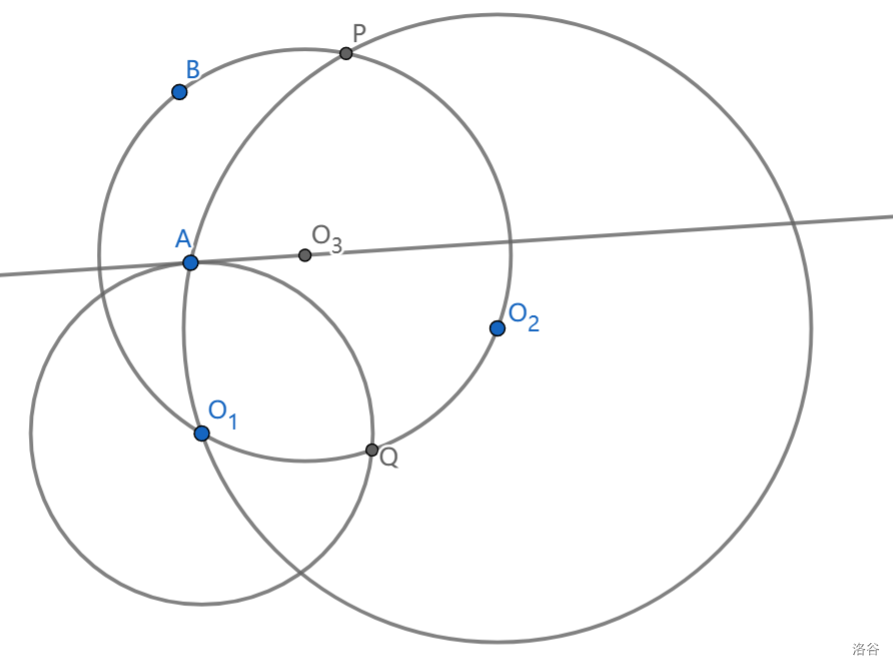
圆 \(c_1\) 的圆心为 \(O_1\) ，圆 \(c_2\) 圆心为 \(O_2\) ，满足 \(O_1\) 在 \(c_2\) 上 ， \(c_1\) 与 \(c_2\) 的一个交点为 \(A\) 。过 \(A\) 作 \(c_1\) 的切线 \(l\) ，\(l\) 上一点 \(O_3\) 为圆心的圆 \(c_3\) 满足 \(O_1,O_2\) 在 \(c_3\) 上， \(c_3\) 与 \(c_2\) 交于 \(P\ne O_1\) ，求证： \(P\) 关于 \(l\) 的对称点在 \(c_1\) 上。

\(P\) 关于 \(l\) 的对称点也在 \(c_3\) 上。设 \(c_3\) 与 \(c_1\) 交点为 \(Q,R\) ，那么只要证 \(P,Q\) 关于 \(l\) 对称即可

取 \(O_1\) 关于 \(l\) 对称点 \(B\) ，它在 \(c_3\) 上，这会帮助我们分析。关于 \(c_1\) 反演。

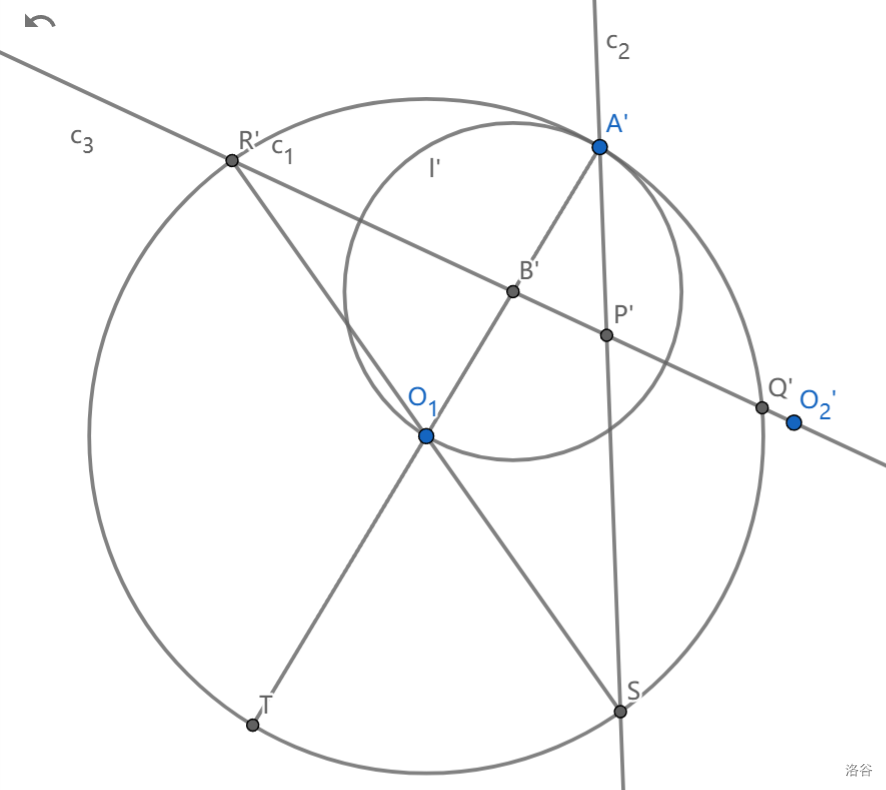
反演之后， \(l\) 变为以 \(O_1A'\) 为直径的圆，圆心是 \(B'\) ， \(c_2\) 变成一条过 \(A'\) 的直线，而 \(O_2'\) 与 \(O_1\) 关于这条直线对称， \(c_3\) 则变成直线 \(O_2'B\) ，与 \(c_1\) 交于 \(R',Q'\) ，两条直线交于 \(P'\)

根据 \(AB'=O_1B'\) 以及 \(R'O_1=A'O_1=A'O_2'\) 可得到 \(O_1O_2'A'R'\) 是平行四边形

\(A'O_1'\cap c_1=T\) ，把 \(R'O_1\) 延长，交圆于 \(S\) ，发现 \(S\) 也在 \(c_2'\) 上，因为 \(\angle TA'S=\frac 12\angle A'O_1'R'=\frac 12 \angle O_1A'O_2'=\angle O_1'A'P'\)

根据我们开始提到的对称在反演下的意义，要证 \(P,Q\) 关于 \(l'\) 反演对应，即 \(B'A'^2=B'P'\cdot B'Q'\)

这是显然的， \(\angle A'Q'B'=\angle SA'R=\angle P'A'B'\) （用到 \(ARTS\) 是矩形）

CP5

我们要谈论 \(Casey\) 定理，这是 \(Ptolemy\) 定理的推广形式。

如图，\(\odot O_1,\odot O_2,\odot O_3,\odot O_4\) 均与 \(\odot O\) 相切，定义 \(l_{ij}\) 是 \(\odot O_i\) 与 \(\odot O_j\) 的公切线，其中

若 \(\odot O_i,\odot O_j\) 均与 \(\odot O\) 内切或外切，则 \(l_{ij}\) 代表外公切线长，反之代表内公切线长。

我们有 \(l_{12}l_{34}+l_{14}l_{23}=l_{13}l_{24}\)

证明异常的简单，关于 \(\odot O\) 反演，四个圆变为一条直线两侧的一些圆，公切线长就是切点之间的距离，很容易验证。

逆定理是已知三个圆相切，可以验证第四个圆是相切的。

一般使用 \(Casey\) 定理时会选择一些圆退化成点圆，而非使用四个圆。

例1

如图，矩形 \(ABCD\) 中，圆 \(c\) 经过 \(A,C\) 两点，圆 \(c_1\) 与 \(CD,AD,c\) 均相切，圆 \(c_2\) 与 \(AB,BC,c\) 均相切，记 \(r_1,r_2\) 表示 \(c_1,c_2\) 的半径， \(r\) 表示 \(\triangle ABC\) 的内切圆半径，求证： \(r_1+r_2=2r\)

对点圆 \(A,C\) 和 \(c_1,c_2\) 关于 \(c\) 用 \(Casey\) 定理。我们看到 \(A\) 与 \(c_1\) ， \(C\) 与 \(c_2\) 的公切线长是 \(b-r_1,b-r_2\) （点圆的公切线不分内外）， \(A,c_2;C,c_1\) 的公切线长是 \(a-r_1,a-r_2\) ，和 \(AC=\frac{a^2+b^2}\) ， \(c_1,c_2\) 内公切线长是 \(\sqrt{(a-r_1-r_2)^2+(b-r_1-r_2)^2-(r_1+r_2)^2}\) （内公切线长^2=圆心距2-半径和^2）

代入 \(r_1+r_2=x\) ，我们看到方程 \(b^2-a^2-(b-a)x=\sqrt{a^2+b^2}\sqrt{(a-x)^2+(b-x)^2-x^2}\) ，是一个令人愉悦的二次方程，解得 \(x=a+b-\sqrt{a^2+b^2}\)

例2

如图， \(c_1,c_2\) 外离且均内切于 \(c\) ， \(c_1,c_2\) 的两条内公切线与 \(c\) 交于 \(AC,BD\) ，求证： \(AB,CD\) 分别平行于 \(c_1,c_2\) 的两条外公切线

我们假设一条外公切线与 \(c\) 相交于 \(P,Q\) ，然后来证明 \(AB//PQ\)

我们先选取 \(c_1,A,B,P\) （注意不要选取 \(c_1,c_2,A,B\) ，不与 \(P,Q\) 相关，这不会产生任何作用）

\(BP\cdot AE=AP\cdot BH+AB\cdot PS\)

然后选 \(c_2,A,B,P\)

\(BP\cdot AG=AP\cdot BF+AB\cdot PT\)

现在可以将两式相减得到

\(BP\cdot GE=-AP\cdot HF+AB\cdot ST\)

我们看到 \(GE=HF=l_{内},ST=l_{外}\)

对 \(Q\) 再用一遍，我们看到

\(BP+AP=BQ+AQ=AB\cdot\frac{l_{外}}{l_{内}}\)

所以在以 \(A,B\) 为焦点的椭圆上，与过 \(A,B\) 的圆的交点，显然平行。

CP5

我们最后再来总结一下反演在什么的情形下比较适合使用：

1. 很多过一个点的圆，这是最常见的

2. 比较奇怪的角条件，不一定是相加的

3. 关于一个点的很多信息，可以试试以这个点为反演中心

4. 一些类似圆幂关系的式子，但是不在一个圆上，可以考虑一个将这两个圆互相对应的反演

5. 正交与相切的圆

6. 一些垂足三角形，内切圆切点三角形内部的点，可以通过反演得到一些条件

7. 想不到其它任何方法的时候

有些题显然不能反演：

1. 直线型问题，到处都是的直线

2. 很多的，到处都是的角关系

例1

这个角度关系，我们关于 \(D\) 作反演就会变成角平分线

但是我们看到 \(<FD,BC>=\angle C'DF'=\angle C'A'F'=Rt\angle-\angle DA'B'\) ，这似乎不是一个很好的角关系

其实不然， \(\angle B'A'C'=B+C\) ，所以 \(\angle B'C'F'=\angle DA'F'=B+C-\frac{\pi}2\) ，而弧 \(B'C'\) 对应的是 \(\angle A\) ，所以延长 \(C'F'\) 交 \((A'B'C')\) 于点 \(G\) ，我们看到了弧 \(C'G\) 对应 \(A+B+C-\frac{\pi}2=\frac{\pi}2\) ，所以它是直径！

现在弧 \(C'A'=C'E'\) 给出了 \(\triangle C'A'F'\cong\triangle C'E'F'\) ，所以要证明 \(\angle DF'E'+\angle E'B'D\) 是定值，我们只要证明 \(2\angle A'F'C'+\angle A'F'D-\angle B'A'D\) （用 \(2\pi\) 减去得到）是定值就好

愉悦的导角给出这个角是 \(\angle B'A'D+\angle B'A'C'=2B+C\) ，完成了证明。

例2

\(\triangle ABC\) 中， \(H\) 为垂心， \(S\) 为 \(\triangle AHC\) 外接圆上一点，满足 \(\angle ASB=Rt\angle\) ， \(P\) 在 \(AC\) 上，满足 \(\angle APS=\angle BAS\) ，证明：直线 \(CS\) ， \((BPC)\) 和以 \(AC\) 为直径的圆共点。

这题的反演痕迹过于明显，我们只是再介绍一下垂心反演的另一种形式：关于 \(A\) 反演， \(H\leftrightarrow D,B\leftrightarrow F,C\leftrightarrow E\)

现在重述 \(S=(AHC)\cap(ABD)\leftrightarrow S'=DE\cap FH\) ， \(\angle AS'P'=\angle BAS=\angle FAS'\) 从而 \(S'P'//AF\)

现在我们要证 \(CS\leftrightarrow (AES'),(BPC)\leftrightarrow (EFP'),(ACD)\leftrightarrow BE\) 共点，因为两个圆已经共点于 \(E\) ，只要证明 \(BE\) 是根轴，我们来证明 \(B\) 在根轴上

我们拥有平行条件，所以想办法刻画这两个圆与 \(AB\) 的交点。如果有一个精确的图当然会更容易，我们会看到做一个平行四边形 \(P'S'UV\) ，会有 \(\angle AUS'=B=\angle S'EC\) ，从而 \(AES'U\) 共圆，并且 \(\angle AVP'=B=\pi-\angle FEP'\) 给出 \(P'VFE\) 共圆

现在要证 \(BU\cdot BA=BV\cdot BF\) ，我们用平行导比例，看到

\(\large \frac{BU}{BF}=\frac{CS'}{CF}=\frac{CP'}{CA}=\frac{BV}{BA}\) ，证毕。