高等数学·函数

函数

定义: 二要素：定义域&对应关系

$$
\begin{align}
&y=f(x),x\in R \Leftrightarrow y=(t),t\in R\
&\int_{a}^{{b}f(t)dt=\int_{a}}f(x)dx\
&\sqrt{x^2}=|x|=(x)^{\frac{1}{2}}\
&-\sqrt{x^2}=-|x|=-(x2)^{\frac{1}{2}}
\end{align}
$$

例题：
$$
\begin{align}
&证明：|\frac{x}{1+x^2}|\leq\frac{1}{2}\
&用a^2+b2\geq 2ab\
&解：|\frac{x}{1+x^2}|\geq|\frac{x}{2x}|=\frac{1}{2}
得证
\end{align}
$$

基本初等函数：

$$
\begin{align}
&常函数:y=c\
&幂函数:y=x^a\
&指数函数:y=a^x\
&对数函数:y=\log_{a}x\
&三角函数:y=\sin x ,y=\cos x,y=\tan x,y=\csc x=\frac{1}{\sin x},y=\sec x=\frac{1}{\cos x},y=\cot x=\frac{1}{\tan x}\
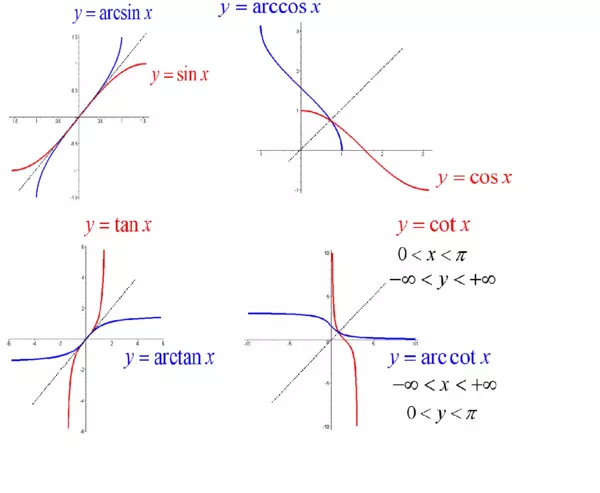
&反三角函数:y=\arcsin x,y=\arccos x,y=\arctan x,y=arccot x
\end{align}
$$

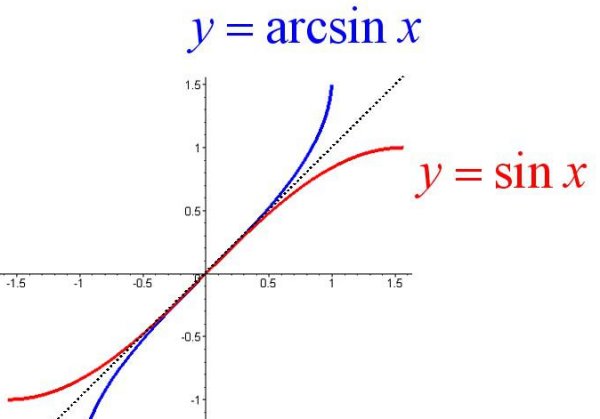
arcsinx&sinx

$$
\begin{align}
&y=\arcsin x,x \in [-1,1],y \in [-\frac{\pi}{2},\frac{\pi}{2}]\
&\arcsin (x+\frac{\sqrt{2}}{2})=+\frac{\pi}{4}\
&\arcsin (x-\frac{\sqrt{2}}{2})=-\frac{\pi}{4}\
&\arcsin (x+1)=+\frac{\pi}{2}\
&\arcsin (x-1)=-\frac{\pi}{2}\
&\arcsin x并不是\sin x的反函数，只是\sin x在x \in [-\frac{\pi}{2},\frac{\pi}{2}]内的逆映射
\end{align}
$$

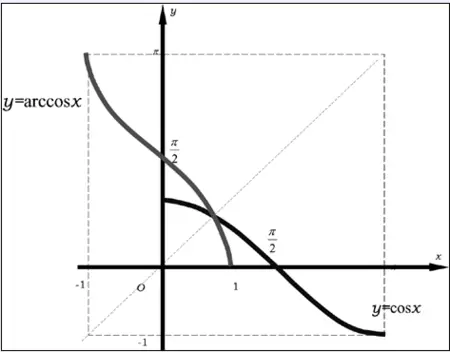
arccosx&cosx

$$
\begin{align}
&y=\arccos x,x \in [-1,1],y \in [0,\pi]\
&\arccos (+1)=0\
&\arccos (-1)=\pi\
&\arccos (\frac{1}{2})=\frac{\pi}{3}\
&\arccos x并不是\cos x的反函数，只是\cos x在x \in [0,\pi]内的逆映射
\end{align}
$$

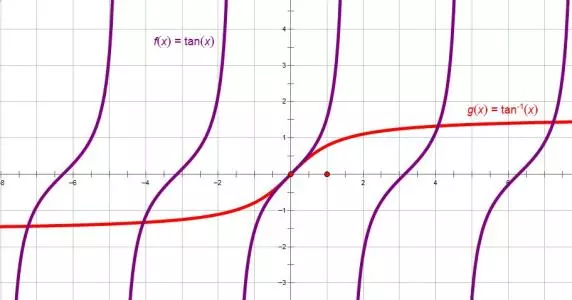
arctanx&tanx

$$
\begin{align}
&y=\arctan x,x \in [-\infty,+\infty],y \in [-\frac{\pi}{2},\frac{\pi}{2}]\
&\arctan (+\infty)=\frac{\pi}{2}\
&\arctan (-\infty)=-\frac{\pi}{2}
\end{align}
$$

arccotx&cotx

$$
\begin{align}
&y=arccot x,x \in [-\infty,+\infty],y \in [0,\pi]\
&\arctan (+\infty)=0\
&\arctan (-\infty)=\pi
\end{align}
$$

$$
\begin{align}
&连续函数存在反函数，其反函数也是连续函数\
&一个可导函数存在反函数，其反函数不一定可导(可导函数x^{3的反函数x}{3}}在0处并不可导)\
\end{align}
$$

常用的三角恒等：
$$
\begin{align}
&\sin^{2}x+\cosx=1 \
&\sin 2x=2\sin x \cos x=\frac{2\tan x}{1+\tan^{2}x}\
&\cos 2x=\cos^{2}x-\sinx=1-2\sin^{2}x=2\cosx-1=\frac{1-\tan^{2}x}{1+\tanx}\
&1+\tan^{2}x=\secx\
&1+\cot^{2}x=\cscx\
&\arcsin x+arccosx=\frac{\pi}{2}(\forall x\in[-1,1])\
&\arctan x+arccot x=\frac{\pi}{2}(\forall x\in(-\infty,+\infty))\
&\arcsin x+\arcsin \sqrt{1-x^2}=\frac{\pi}{2}(\forall x\in[0,1])\
&\arctan x+\arctan \frac{1}{x}=\frac{\pi}{2}(\forall x \in(-\infty,0)\cup(0,+\infty))
\end{align}
$$

函数性质

1）奇偶性

$$
\begin{align}
&奇函数:f(-x)=-f(x),偶函数f(-x)=f(x)\
&f,g为奇函数，f(g(x))为奇函数还是偶函数？\
&用定义:\
&f(g(-x))=f(-g(x))=-f(g(x))\Leftrightarrow f(g(x))是奇函数
\end{align}
$$

判断奇偶性的方法：

（1）定义

（2）奇偶函数的四则运算：奇函数代数和为奇函数，偶函数的代数和为偶函数，奇函数和偶函数的乘积为奇函数

（3）奇函数的复合运算：内外函数至少一个为偶函数，则复合函数为偶函数，奇函数与奇函数复合为奇函数

（4）奇函数的导数为偶函数，偶函数的导函数为奇函数，奇函数的原函数为偶函数，但偶函数的原函数未必为奇函数
$$
f(x)=1,F(x)=x+1,\int_{0}^{x}f(t)dt为奇函数
$$

2）周期性

3）单调性

初等函数

由基本初等函数经四则运算以及复合运算后得到的函数

一个初等函数的绝对值还是初等函数

函数有界性

$$
\begin{align}
&有界\Leftrightarrow 上下有界\
&无界\Leftrightarrow 上下界1个或没有
\end{align}
$$

判定有界性方法：
$$
\begin{align}
&1)定义，对函数的绝对值放大不等式，直到某一正常值，按最值得到函数有界\
&2)若f(x)在D1,D2上均有界，则在D1\cup D2上也有界\
&3)闭区间上的连续函数一定是有界的(开区间上的连续函数不一定是有界\tan x)\
&4)收敛数列必有界\
&5)存在极限的函数局部有界\
&\lim_{x \rightarrow x_0}f(x)\Rightarrow f(x)必在x_0的某空心邻域内有界\
&\lim_{x \rightarrow +\infty}f(x)\Rightarrow 必存在M,使f(x)在(M,+\infty)内有界
\end{align}
$$

判定函数无界方法：
$$
\begin{align}
&无穷大量必无界(lim_{x\rightarrow \frac{\pi}{2}}\tan x=\infty)\
&局部无界必整体无界(f(x)=x\sin x)
\end{align}
$$
例题：
$$
\begin{align}
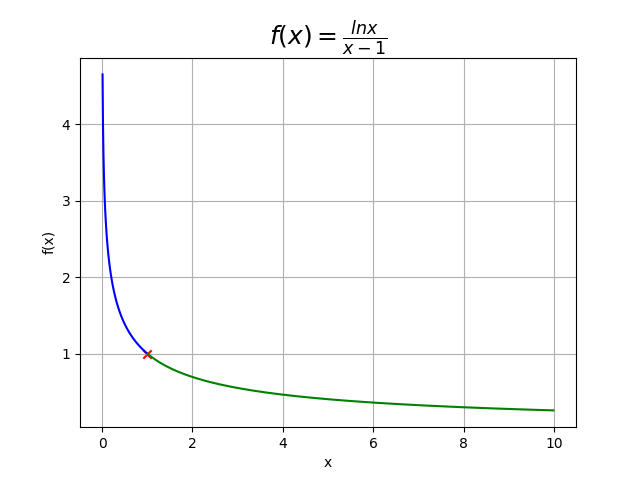
&证明：f(x)=\frac{\ln x}{x-1}在(0,1)内无界，在(1,+\infty)内有界\
&证：\lim_{x\rightarrow0^{+}}f(x)=+\infty \Rightarrow f(x)在(0,\epsilon)内无界 \Rightarrow f(x)在(0,1)内无界\
&\lim_{x\rightarrow1^{+}}f(x)=1,从而\exist \epsilon0,使f(x)在(1,1+\epsilon)内有界\
&\lim_{x\rightarrow+\infty}f(x)=0,从而\exist M1+\epsilon,使f(x)在(1,+\infty)内有界\
&又由f(x)在[M,+\infty]上连续，从而有界，使得f(x)在(1,+\infty)内有界
&
\end{align}
$$

$$
\begin{align}
&注解：f(x)在(1,1)处无定义，导致f(x)在全局不连续，需要分类讨论\
&在x\rightarrow0^+时，在该空心邻域(0,\epsilon)内函数极限等于+\infty,故领域内无上界，可推出邻域内无界，进一步可推出f(x)在(0,1)无界\
&在x\rightarrow1^+时，在该空心领域(1,1+\epsilon)内函数极限等于1，故领域内有上界，在x\rightarrow +\infty时,函数在邻域内极限等于0又由于f(x)在[1,+\infty)内为连续函数，可以推出在x\in [1,+\infty)f(x)
\end{align}
$$

复合函数

$$
y=f(u),u=g(x) ,y\leftarrow g\leftarrow x(逐一传递)
$$

例题：
$$
\begin{align}
&f(\sqrt[3]{x}-1)=x-1,求f(x)\
&解：设u=\sqrt[3]{x}-1\
&x=(u+1)^3,f(u)=(u+1)3-1\
&f(x)=(x+1)^3-1\
& \
&注解：凑右侧表达式(反解很难时)\
\end{align}
$$

反函数

注解：
$$
\begin{align}
&1.一一对应的函数有反函数，从而区间上的严格单调必有反函数\
&y=\sin x无反函数，但y=\sin x,x\in[-\frac{\pi}{2},\frac{\pi}{2}]\
&2.函数x=f^{{-1}(y)与y=f}(x)为同一函数，前者图像与y=f(x)相同，后者图像与y=f(x)关于y=x对称\
&3.对于\forall x\in D,f^{-1}(f(x))=x;当y\in f(D)时,有f(f^{-1}(y))=y
\end{align}
$$
例题：
$$
\begin{align}
&\arcsin (\sin \theta)=\frac{\pi}{4},且\theta \in(\frac{\pi}{2},\pi),求\theta=?\
&解：\theta \in (\frac{\pi}{2},\pi) \Rightarrow \pi-\theta \in (0,\frac{\pi}{2}) \
&\arcsin (\sin(\pi - \theta))=\frac{\pi}{4} \Rightarrow \pi - \theta=\frac{\pi}{4}\
&\theta=\frac{3\pi}{4}
\end{align}
$$