My Blogs
下文中 \([n]\) 表示 \(\{1,2,3\dots n\}\)。
P0
对于正整数 \(n\),称 \(a_{1\dots k}\) 是 \(n\) 的有序划分,当且仅当 \(\sum_i a_i=n\)。给定 \(n(\geq 2)\),求满足 \(\sum_{i}[2|a_i]\) 是偶数的有序划分个数。
答案:\(2^{n-2}\)。
\(n\) 的所有划分可以看成有 \(n-1\) 个空位,每个空位可以放板或不放,总方案数是 \(2^{n-1}\)。现在只需要证明偶数的个数一半是奇,一半是偶。
对于一个有序划分,若 \(a_1=1\),则把 \(a_1\) 和 \(a_2\) 合并在一起。否则把 \(a_1\) 拆成 \(1\) 和 \(a_1\)。经过这样的操作,一定会改变偶数个数的奇偶性。
上述映射是一个 对合,即 \(f=f^{-1}\)。这样就证明了奇偶两边的数量相等。
注意构造对合的时候不能映射到自己。
P1
\[\sum_{k=0}^m\binom{m+k}{k}2^{-k} \]
答案是 \(2^m\)。考虑一个长度为 \(2m\) 的 \(01\) 序列,显然有 \(2^{2m}\) 种。变形一下上式:
\[\sum_{k=0}^m\binom{m+k}{k}2^{m-k} \]对于一个序列,若 \(0,1\) 都出现了 \(m\) 次,对应 \(k=m\),其方案数为 \(\binom{2m}{m}\)。
否则考虑枚举二者中较多的第 \(m+1\) 次出现位置,则前 \(m+k\) 个需要填 \(m\) 个,\([m+k+2,2m]\) 随便填,然后还需要确定众数是谁(\(m+k+1\) 上填什么),就得到了上式。
P2
\[\sum_{k=0}^n\binom{2k}{k}\binom{2n-2k}{n-k} \]
答案是 \(4^n\)。两个上指标的和是 \(2n\),两个下指标的和是 \(n\),看成是平面直角坐标系上从 \((0,0)\) 开始走的路径计数。
把 \(\binom{2k}{k}\) 看成是枚举和 \(y=x\) 的最后一个交点。设 \(m=n-k\),假设下一步向右走,走到 \(y=2n-x\) 直线上并且不走到 \(y=x\) 上的方案数可以用计算类似卡特兰数的方式计算:
\[\sum_{i=0}^{m-1}\binom{2m-1}{i}-\binom{2m-1}{i-1}=\binom{2m-1}{m-1} \]第一步也可以向上走,方案数一样,\(2\binom{2m-1}{m-1}=\binom{2m}{m}\)。所以就是任意走 \(2n\) 步的方案数。
P3
\[\sum_{i\geq 0}\binom{x+y+i}{i}\binom{y}{a-i}\binom{x}{b-i} \]
答案是 \(\binom{x+a}{b}\binom{y+b}{a}\)。在两边同时乘一个 \(\binom{x+y}{x}\)。
\[\sum_{i\geq 0}\binom{x+y+i}{x,y,i}\binom{y}{a-i}\binom{x}{b-i}=\binom{x+y}{y}\binom{x+a}{b}\binom{y+b}{a} \]集合是这样的形式:
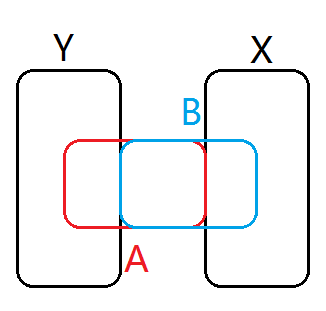
其中 \(\lvert A\rvert=a,\lvert B\rvert=b,\lvert X\rvert=x,\lvert Y\rvert=y,\lvert A\cap B\rvert=i\),则左式比较平凡,先确定 \(x,y,i\),各含有多少各元素,然后确定 \(A,B\) 在 \(X,Y\) 中的部分。
若 \(T\subseteq S\),且对于 \(i\in[1,\lvert T\rvert]\),确定了在 \(T\) 中第 \(i\) 大的元素在 \(S\) 中是第几大,则称确定了信息 \((T,S)\)。
右式相当于确定了信息 \((X,X\cup Y),(B,X\cup A),(A,Y\cup B)\),至于要证明通过这三组信息可以确定一个全序关系(即可以排序所有元素)。
考虑每次寻找最小的元素。首先根据 \((X,X\cup Y)\) 中的信息,可以确定最小值一定不在 \(X\) 或者 \(Y\)。假设不在 \(Y\)(不在 \(X\) 同理):
若 \(X\cup A\) 的最小值在 \(B\) 中,那么若 \(Y\cup B\) 的最小值在 \(A\) 中,则最小值就在 \(A\cap B\) 中,否则在 \(B\setminus (A\cap B)\) 中。
否则在 \(X\setminus B\) 中。
上面这一过程没有信息的浪费(???),所以映射是单的。
P4
\[\sum_{k=0}^n\binom n k^2x^k=\sum_{k=0}^n\binom{2n-k}{n-k,n-k,k}(x-1)^k \]
右式可以变成 \(\binom n k\binom{2n-k} n(x-1)^k\)。
左式的组合意义是:\(S,T\subseteq [n],\lvert S\rvert=\lvert T\rvert,f:S\rightarrow[x]\) 的元组 \(A:(S,T,f)\) 数量。
右式的组合意义是 \(S\subseteq[n],T\subseteq[2n]\setminus S,\lvert T\rvert=n,f:S\rightarrow [x-1]\) 的元组 \(B:(S,T,f)\) 数量。
建立双射 \(F:A\rightarrow B\):
对于左式中的 \((S,T,f)\),构造 \(S'=\{y\in S|f(y)!=x\},f'(x)=f(x),T'=\{y\in[n]|y\notin S\}\cup(n+T)\)。注意到因为 \(a\in S'\) 中不含 \(f(a)=x\) 的 \(a\),所以映射 \(f'\) 合法。显然 \(\lvert T'\rvert=n\)。
这种映射对于不同的 \(A\),显然会映射到唯一的 \(B\)。
\(F':B\rightarrow A\):
对于右式中的 \((S,T,f)\),构造 \(T'=\{x-n|x\in T,x>n\}\),\(S'=[n]\setminus T\),\(f'(a)=\begin{cases}f(a)\;\; a\in S \\ x\qquad a\notin S\end{cases}\),这样仍然只会映射到唯一的 \(A\)。
P5.1
\(A\) 是 \(n\) 的有序划分,求:
\[\sum_{A\;\text{is}\;\text{valid}}\prod_{j=1}^ka_j \]
答案是 \(F_{2n-1}\),\(F\) 是斐波那契数列。
考虑画出 \(n\) 个圆圈,每两个圆圈中间画一个点,共 \(2n-1\) 个元素,然后选择 \(2n-1\) 个元素的一个子集,使得 第一个选的和最后一个选的都是圆圈,并且每两个选择的圆圈间恰有一个点被选择。
这样一个点就代表一个隔板,把 \(n\) 分隔成了若干份,每一份有 \(a_i\) 个圆圈,每个要段中要再选一个,贡献就是乘起来。
可以等价于把 \(2n-1\) 分成若干个 \(1,2\),选择所有大小为 \(1\) 的块包含的元素,就是斐波那契数列。
P5.2
\(A\) 是 \(n\) 的有序划分,求:
\[\sum_{A\;\text{is}\;\text{valid}}\prod_{j=1}^k(2^{a_j-1}-1) \]
答案是 \(F_{2n-3}\),其中 \(F\) 是斐波那契数列。
首先考虑怎么把 \(2^{a_i-1}-1\) 和划分成 \(1,2\) 的段找到联系。
对于一个 \(a_i\),考虑把 \(2a_i\) 划分成若干段,每段的长度是 \(1\) 或 \(2\)。满足:
-
首段长为 \(1\),末段长为 \(2\)。
-
设长为 \(1\) 的段有 \(k\) 段,则 \(k\) 是偶数,并且对于 \(1\sim k-1\) 中的每个偶数 \(z\),第 \(z\) 个 \(1\) 后面也是 \(1\)。
这样的方案数就是 \(2^{a_i-1}-1\),考虑去掉开头的第一个 \(1\) 和结尾的 \(2\),然后在最后一个 \(1\) 后面填一个 \(1\),这样就是有一个长度为 \(2a_i-3+1\) 的段,没相邻两个为一组,每组可以是 \(\{1,1\}\) 或者是 \(\{2\}\),并且不能全部是 \(\{2\}\),所以答案就是 \(2^{a_i-1}-1\)。
然后对于一个数,考虑把所有 \(a_i\) 的拆分段拼起来形成一个和为 \(2n\) 的 \(1,2\) 序列。因为开头的 \(1\) 和末尾的 \(2\) 是固定的,所以方案数是 \(F_{2n-3}\)。
现在证明每一个序列都对应唯一的划分方式。首先 \(1\) 的总个数一定是偶数。执行这样一个过程:从前向后,不断找到满足下一位是 \(1\) 并且前面的 \(1\) 的个数是偶数的第一个 \(2\) 并作为一个划分的结尾。
P6(模拟赛题)
求
\[f(n)=\sum_{m=0}^n\sum_{k=m}^n\binom k m\binom{k-m}{\lfloor\frac{k-m} 2\rfloor}2^{n+m-k} \]要求 \(\mathcal O(n)\)
整理一下式子:
\[\sum_{k=0}^n2^{n-k}\sum_{m=0}^k\binom k m\binom{k-m}{\lfloor\frac {k-m} 2\rfloor}2^m \]问题转为求后半部分 \(g(n)=\sum_{m=0}^n\binom n m\binom{n-m}{\lfloor\frac {n-m} 2\rfloor}2^m\)。
考虑 \(S=[2n+1]\) 中 \(1\) 和 \(2\) 匹配,\(3\) 和 \(4\) 匹配 \(\dots\) \(2k-1\) 和 \(2k\) 匹配(\(k\leq n\)),\(2n+1\) 没有匹配。
对于 \(x\leq 2n\) 记 \(x\) 的匹配为 \(m(x)\)。
选取 \(T\subseteq S\) 使得 \(\lvert T\rvert=n\)。对于每种方案,记 \(R=\{x|x\in T,x\not= 2n+1,m(x)\notin T\}\),设 \(\lvert R\rvert=k\),则 \(T\) 内部有 \(\frac{n-k} 2\) 对匹配。这样就有了组合意义:
先确定 \(n\) 对匹配中 \(k\) 个恰好只被选入一个到 \(T\) 中,并且决定是哪个被选入,方案数是 \(\binom n k 2^k\)。
剩下的部分还要选 \(\lfloor \frac{n-k}{2}\rfloor\) 对匹配,方案数是 \(\binom{n-k}{\lfloor \frac{n-k}{2}\rfloor}\)。
然后如果 \(n-k\) 是奇数,就把 \(2n+1\) 选进去,否则不选,这样集合大小一定能凑成 \(n\)。所以答案就是 \(g(n)=\binom{2n+1}{n}\)。预处理组合数,预处理前缀和可以做到 \(\mathcal O(n)\)。
标签:双射,rvert,sum,构造,lvert,2m,2n,初等,binom From: https://www.cnblogs.com/WrongAnswer90/p/18138159