P1149 [NOIP2008 提高组] 火柴棒等式

题目

给你 \(n\) 根火柴棍，你可以拼出多少个形如 \(A+B=C\) 的等式？等式中的 \(A\)、\(B\)、\(C\) 是用火柴棍拼出的整数（若该数非零，则最高位不能是 \(0\)）。用火柴棍拼数字 \(0\sim9\) 的拼法如图所示：

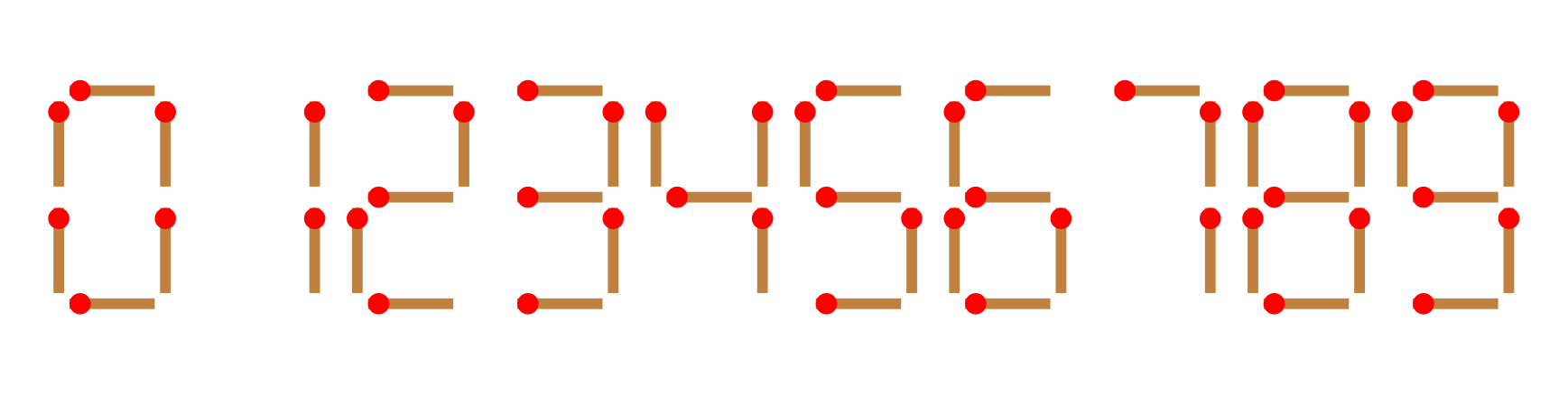
注意：

1. 加号与等号各自需要两根火柴棍；
2. 如果 \(A \ne B\)，则 \(A+B=C\) 与 \(B+A=C\) 视为不同的等式（\(A,B,C \ge 0\)）；
3. \(n\) 根火柴棍必须全部用上。

输入

一个整数 \(n(1 \leq n\leq 24)\)。

输出

一个整数，能拼成的不同等式的数目。

样例 1

输入

14

输出

2

样例 2

输入

18

输出

9

提示

【输入输出样例 1 解释】

\(2\) 个等式为 \(0+1=1\) 和 \(1+0=1\)。

【输入输出样例 2 解释】

\(9\) 个等式为

\(0+4=4\)、\(0+11=11\)、\(1+10=11\)、\(2+2=4\)、\(2+7=9\)、\(4+0=4\)、\(7+2=9\)、\(10+1=11\)、\(11+0=11\)。

思路一

首先，根据题意可知，火柴棒的个数最多为 \(24\) 根，除去“+”和“=”占用的 \(4\) 根火柴棍，那么剩下 \(20\) 根火柴棍。在 \(0\) 到 \(9\) 这 \(10\) 个数字中，可以看到数字 \(1\) 需要用到的火柴棍最少，只需要 \(2\) 根火柴棍。所以 \(20\) 根火柴棍最多能组成 \(10\) 个 \(1\)。在 \(4\) 位数里 \(1111\) 用的火柴棍最少也要 \(8\) 个，所以构造的形如 \(a+b=c\) 的火柴棍等式就转换为“\(1111+x=(1111+x)\)”，在这个等式中 \(a,b,c\) 的任意一个数都不能超过 \(1111\)，这里设 \(n=1111\)。假设已知等式的加数，该加数的范围是 \(0\) 到 \(n\)，接下来分别枚举 \(a,b\) 的值。\(c\) 可以通过 \(a+b\) 算出来，无须枚举。约束条件是：\(a\) 所使用的火柴棍的根数加上 \(b\) 所使用的火柴棍的根数，再加上 \(c\) 所使用的火柴棍的根数，如果恰好等于 \(m-4\)，则成功地找出了一组等式。

代码

#include <bits/stdc++.h>

using namespace std;

int a, b, c, m, sum;

int f(int x) // 用来计算一个数需要用火柴棍的总数
{
	int s = 0, f[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
	while (x / 10 != 0)
	{
		s += f[x % 10];
		x /= 10;
	}
	s += f[x]; // 加上最后的数字对应的根数
	return s; // 返回火柴棍的总跟数
}

int main()
{
	cin >> m;
	for (a = 0; a <= 1111; a ++ )
	{
		for (b = 0; b <= 1111; b ++ )
		{
			c = a + b;
			if (f(a) + f(b) + f(c) == m - 4)
				sum ++;
		}
	}
	cout << sum << '\n';
	return 0;
}

思路二

上述算法的时间复杂度位 \(O(n^2 \times\)数字分离的次数\()\)，由于数字最大是 \(1111\)，每个数字分离的次数最大是 \(4\)，完整算法 \(1s\) 之内可以输出答案。但是由于每个数字都要分离计算数字需要的所有火柴棍数目，这样导致很多数字重复计算，加大了时间复杂度。思考之后可以将 \(0\) 到 \(2222\) 的所有整数需要的火柴棒数目预处理保存在数组中。那么难点是如何更快速地预处理出 \(0\) 到 \(2222\) 中所有数字的火柴棒数目，可以使用递推算法。设 \(s \lbrack i \rbrack\) 数组表示数字 \(i\) 需要的火柴棒数目，那么 \(s \lbrack i \rbrack = s \lbrack i/10 \rbrack + s \lbrack i \% 10 \rbrack\)，时间复杂度是 \(O(n)\)。整个算法总时间是 \(O(n^2)+O(n)\)，更为优秀。

代码

#include <bits/stdc++.h>

using namespace std;

int f[2500] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}, a, b, c, m, sum;

int main()
{
	cin >> m;
	for (int i = 10; i <= 2222; i ++ )
		f[i] = f[i / 10] + f[i % 10];
	for (a = 0; a <= 1111; a ++ ) // 枚举 a 和 b
	{
		for (b = 0; b <= 1111; b ++ )
		{
			c = a + b;
			if (f[a] + f[b] + f[c] == m - 4)
				sum ++;
		}
	}
	cout << sum << '\n';
	return 0;
}