[HNOI2012] 矿场搭建
前置知识: #Tarjan求点双连通分量
题目大意
给你一张无向连通图,任意删去其中一个点,要求在删点后在每个连通块中有一个点被选择,问至少需要选择多少个点,以及选择的方案数。
输入输出格式
输入
多组数据以\(N=0\)结束
每组数据第一行为边的数量\(N \ (N \leq 500)\)
接下来\(N\)行,每行两个整数\(S\)和\(T\),表示一条边连接的两个点。\((1\le S,T \le 10^3)\)
输出
对于每组数据输出一行两个数,表示至少需要选择多少个点,以及选择的方案数。
样例输入
9
1 3
4 1
3 5
1 2
2 6
1 5
6 3
1 6
3 2
6
1 2
1 3
2 4
2 5
3 6
3 7
0
样例输出
Case 1: 2 4
Case 2: 4 1
思路
删除一个点会使无向图中联通块发生变化的只有割点,而不受割点影响的只有点双连通分量,所以我们可以求出所有割点和点双连通分量,再对每一个点双连通分量进行分类讨论。
分类讨论:
\(Ⅰ\)
当一个点双连通分量中没有割点时,就需要选择两个点以防其中的一个点被删除,因为不能从割点连通到另一
个点双连通分量。
对最少选择的点数\(ans1\)的贡献为\(2\),对选择的方案\(ans2\)的贡献为\(ans2 \cdot \frac{size*(size-1)}{2} \ (size为点双连通分量的大小)\)
\(Ⅱ\)
当一个点双连通分量中有一个割点时,只需要选择除割点外的任一点,因为如果删除割点,这个点双连通分量中有一个点被选择,如果删除我们选择的那个点,我们可以从割点连通另一个点双连通分量。
对最少选择的点数\(ans1\)的贡献为\(1\),对选择的方案\(ans2\)的贡献为\(ans2 \cdot size \ (size为点双连通分量的大小)\)
\(Ⅲ\)
当一个点双连通分量中有两个及以上割点时,无论删除哪一个割点,我们可以从剩下的割点连通另外的点双连通分量。
对最少选择的点数\(ans1\)的贡献为\(0\),对选择的方案\(ans2\)的贡献为\(ans2 \times 1\)
输入
9
1 3
4 1
3 5
1 2
2 6
1 5
6 3
1 6
3 2
输出
Case 1: 2 4
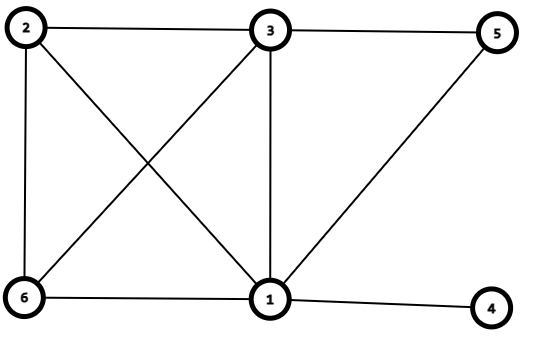
(提问时间 3-5min)
\(Code\)
#include<bits/stdc++.h>
using namespace std;
inline long long read(){
long long x=0,w=0;char c=0;
while(!isdigit(c)) {w|=c=='-';c=getchar();}
while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
return w?-x:x;
}
long long T,n,h[1050],t;
struct node{
long long to;
long long nex;
}e[1050];
inline void add(long long x,long long y){
e[++t].to=y;
e[t].nex=h[x];
h[x]=t;
}
long long dfn[1050],low[1050],cnt,num,ans1,ans2;
bool vis[1050],flag[1050];
stack<long long> st;
vector<long long> dcc[1050];
void tj(long long x){
dfn[x]=low[x]=++num;
vis[x]=1;
st.push(x);
long long son=0;
for(long long i=h[x];i;i=e[i].nex){
long long v=e[i].to;
if(!dfn[v]){
tj(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]){
son++;
if(x!=1||son>1){
flag[x]=1;
}
cnt++;
long long y;
do{
y=st.top();
st.pop();
dcc[cnt].push_back(y);
}while(y!=v);
dcc[cnt].push_back(x);
}
}
else{
low[x]=min(low[x],dfn[v]);
}
}
}//求点双连通分量和割点
int main(){
while(1){
n=read();
if(n==0){
break;
}
T++;
num=cnt=ans1=t=0;
ans2=1;
memset(h,0,sizeof(h));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(vis,0,sizeof(vis));
memset(flag,0,sizeof(flag));
for(long long i=1;i<=1010;i++){
dcc[i].clear();
}
while(st.size()){
st.pop();
}
for(long long i=1,x,y;i<=n;i++){
x=read();
y=read();
add(x,y);
add(y,x);
}
tj(1);
for(int i=1;i<=cnt;i++){
int s1=dcc[i].size(),s2=0;
for(int j=0;j<s1;j++){
s2+=flag[dcc[i][j]];
}
if(s2==1){//分类讨论Ⅱ
ans1++;
ans2*=(s1-1);
}
if(s2==0){//分类讨论Ⅰ
ans1+=2;
ans2*=(s1*(s1-1)/2);
}
}
printf("Case %lld: %lld %lld\n",T,ans1,ans2);
}
return 0;
}
\(Warning\)
因为讲完后有同学对代码的一些地方不理解,所以在这里对其正确性进行证明。
聚焦代码
void tj(long long x){
dfn[x]=low[x]=++num;
vis[x]=1;
st.push(x);
long long son=0;
for(long long i=h[x];i;i=e[i].nex){
long long v=e[i].to;
if(!dfn[v]){
tj(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]){
son++;
if(x!=1||son>1){
flag[x]=1;
}
cnt++;
long long y;
do{
y=st.top();
st.pop();
dcc[cnt].push_back(y);
}while(y!=v);
dcc[cnt].push_back(x);
}
}
else{
low[x]=min(low[x],dfn[v]);
}
}
}
因为正常的 \(tarjan\) 和 \(树\) 的遍历都会判掉\(father\)节点
void tj(long long x,long long fa){//change
dfn[x]=low[x]=++num;
vis[x]=1;
st.push(x);
long long son=0;
for(long long i=h[x];i;i=e[i].nex){
long long v=e[i].to;
if(v==fa){
continue;
}//change
if(!dfn[v]){
tj(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]){
son++;
if(x!=1||son>1){
flag[x]=1;
}
cnt++;
long long y;
do{
y=st.top();
st.pop();
dcc[cnt].push_back(y);
}while(y!=v);
dcc[cnt].push_back(x);
}
}
else{
low[x]=min(low[x],dfn[v]);
}
}
}
但不判父节点的写法其正确性是可以保证的。
\(Part \ 1\)
else{
low[x]=min(low[x],dfn[v]);
}
首先这里并不会递归到它的父亲节点,所以不会出现反复横跳的情况,时间复杂度得到了保证。
\(Part \ 2\)
if(!dfn[v]){
tj(v);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]){
..............
}
}
因为\(tarjan\)算法由递归实现,所以一个节点必然是先求出它的 \(dfn \ 和 \ low 值\) 然后再影响它的父亲进行割点判断。
那么对于 \(low[x]=min(low[x],dfn[v]);(v为x的father时)\)
有两种情况
\(Ⅰ\)
\(low[x]\) 从其它的 \(v\) 里转移来的值小于等于 \(dfn[v](v为x的father)\)
此时 \(low[x]=min(low[x],dfn[v]);(v为x的father时)\) 可以忽略
\(Ⅱ\)
\(low[x]\) 从其它的 \(v\) 里转移来的值大于 \(dfn[v](v为x的father)\)
此时 \(low[x]=min(low[x],dfn[v]);(v为x的father时)\) ,那么\(low[x]=dfn[v]\)
此时我们回溯到上一层(就是 \(x\) 的 \(father\) ),由于判断时是 \(low[v]>=dfn[x]\) 所以还是会进入\(if内部语句\)。
所以不会对答案产生影响
总结
综上所述,不判 \(father\) 节点不会出现问题。
而且,按照我们的推理,\(low[x]\) 只会小于或等于 \(dfn[fa]\) ,因为 \(low[x]\) 比 \(dfn[fa]\) 大,语句\(low[x]=min(low[x],dfn[v])\)就会起效。
所以我们将 \(if(low[v]>=dfn[x])\) 改为 \(if(low[v]==dfn[x])\) 也不会出问题。