NOI2021 轻重边
题目链接:#4812. [NOI2021] 轻重边
前置知识 : #树链剖分 #线段树
题目大意
给定\(n\)个点组成的树,\(m\)次操作。
修改操作会让路径\(a \to b\)上的所有点的所有连边对答案的贡献变为\(0\),路径\(a \to b\)的所有边的贡献变为\(1\);
查询操作则统计路径\(a \to b\)的答案贡献。(树中一开始答案贡献为\(0\))。
输入格式
第\(1\)行,输入\(T\),表示有\(T\)组数据。
每组数据
第\(1\)行,输入\(n,m\)表示有\(n\)个点和\(m\)个操作。
第\(2-n\)行,每行输入\(u,v\)表示树的一条边。
第\(n+1-n+m\)行,每行输入\(op,a,b\)表示操作信息\((op=1为修改,op=2为查询)\)
输入样例
1
7 7
1 2
1 3
3 4
3 5
3 6
6 7
1 1 7
2 1 4
2 2 7
1 1 5
2 2 7
1 2 1
2 1 7
输出样例
1
3
2
1
数据范围
对于所有测试数据:\(T≤3,1≤n,m≤10^5\)。
| 测试点编号 | \(n,m \le\) | 特殊性质 |
|---|---|---|
| \(1 \sim 2\) | \(10\) | 无 |
| \(3 \sim 6\) | \(5000\) | 无 |
| \(7 \sim 8\) | \(10^5\) | \(A,B\) |
| \(9 \sim 10\) | \(10^5\) | \(A\) |
| \(11 \sim 14\) | \(10^5\) | \(B\) |
| \(15 \sim 16\) | \(2 \times 10^4\) | 无 |
| \(17 \sim 20\) | \(10^5\) | 无 |
思考
感觉每次修改操作对答案的贡献是单独的,前面的修改操作不会影响的后面修改操作对答案的贡献 (就是不会让后面的操作与前面的操作产生额外贡献)。
比如样例
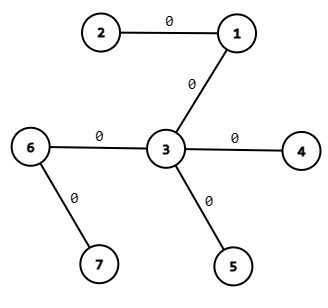
经过第一个操作后\(\Huge \downarrow\)
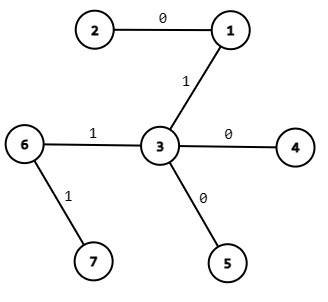
所以操作具有无后效性,如果后面的操作与前面的操作重合,那么会统计后面的操作贡献,前面的操作会无效。
所以我们只需要单独考虑每一次修改操作,使其拥有单独的统计答案的方式。
那么可以给每个修改操作路径上的点打上时间戳,若边连接两点的时间戳相同,则该边的贡献为 \(1\) ,否则为 \(0\) 。
可以简单证明一下操作的正确性,每次修改操作会让路径 \(a \to b\) 上的所有点的所有连边对答案的贡献变为 \(0\),路径 \(a \to b\) 的所有边的贡献变为 \(1\) ,就相当于把这一条链单独拎出来,将其边权修改为 \(1\) 。
而将这条链打上单独的时间戳,既可以起到方便统计答案的作用,又可以和其它修改操作进行区分。然后为了实现后面操作对前面操作的覆盖,我们只记录节点当前的时间戳。
然后统计答案的操作
两个相同的点权贡献答案,感觉和「SDOI2011」染色有点像,不同的是这道题每两个点时间戳相同就贡献一次,而染色是每两个点时间戳不同就贡献一次。
部分分1
#树 #LCA
对于前\(1\sim 6\)个测试点,\(n,m \le 5000\),完全可以接受 \(\mathcal{O}(n \cdot m)\) 的时间复杂度。
直接进行暴力修改每个节点的时间戳和遍历整棵树统计答案即可。
时间复杂度 \(\mathcal{O}(T \cdot nm)\) 期望得分\((30 \ points)\) (实际上因为常数小第\(15-16\)个点也可以过) (实际得分 \(40 \ points\))
关键代码
//倍增求lca
void dfs(int x,int fa){
f[x][0]=fa;
dep[x]=dep[fa]+1;
for(int i=1;i<20;i++){
f[x][i]=f[f[x][i-1]][i-1];
}
for(int i=h[x];i;i=e[i].nex){
int v=e[i].to;
if(v==fa){
continue;
}
dfs(v,x);
}
}
int lca(int x,int y){
if(dep[x]<dep[y]){
swap(x,y);
}
for(int i=19;i>=0;i--){
if(dep[f[x][i]]>=dep[y]){
x=f[x][i];
}
}
if(x==y){
return x;
}
for(int i=19;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
//修改操作,枚举每个点暴力修改
if(op==1){
int LCA=lca(a,b);
c++;
for(int i=a;i!=LCA;i=f[i][0]){
w[i]=c;
}
for(int i=b;i!=LCA;i=f[i][0]){
w[i]=c;
}
w[LCA]=c;
}
//查询操作,枚举每个点暴力判断
if(op==2){
int LCA=lca(a,b);
int ans=0;
for(int i=a;i!=LCA;i=f[i][0]){
if(w[i]&&w[i]==w[f[i][0]]){
ans++;
}
}
for(int i=b;i!=LCA;i=f[i][0]){
if(w[i]&&w[i]==w[f[i][0]]){
ans++;
}
}
printf("%d\n",ans);
}
部分分2
#线段树 #DFS序
对于\(7 \sim 10\)个测试点,树的形态是一条链,那么我们直接用\(DFS序\)的方式将树转为区间问题,直接用线段树维护即可。
时间复杂度 \(\mathcal{O}(T \cdot m \log_2 n)\)
我们把操作放在区间上来分析是如何合并的。
设 \(w[i]\) 代表第 \(i\) 点的时间戳,\(s[i]\) 表示线段树的点 ,我们设 \(s[i].l \ 和 \ s[i].r \ 分别为 \ s[i]\) 代表的区间左右端点,而 \(s[i]\) 的信息会从\(s[2*i] \ 和 \ s[2*i+1] \ 转移过来\) 。
我们在 [[#思考]] 中已经提到过每两个点相同就贡献一次,而两个子节点内部已经统计过,直接转移即可。
会产生变化的只有两个子节点交界的地方,所以我们需要记录区间左右端点的时间戳,进行判断。
struct tree{
int l=0;//区间左端点
int r=0;//区间右端点
int lx=0;//区间左端点颜色
int rx=0;//区间右端点颜色
int lazy=0;//懒标记
int w=0;//区间内答案贡献
tree operator +(const tree&a)const{//重载运算符,区间合并
tree res;
res.l=l;
res.lx=lx;//左儿子的左端点是区间左端点
res.r=a.r;
res.rx=a.rx;//右儿子的右端点是区间右端点
res.w=w+a.w;
if(rx==a.lx&&rx){//warning 当没有时间戳时不统计答案
res.w++;
}
return res;
}//warning 记住结构体中的每个元素都要赋值,就算不变也要在赋值一遍,因为使用时是直接s[k]=s[ls]+s[rs]的赋值操作,如果不每个元素都要赋值可能导致使用的值丢失,让程序错误。
}s[500050];
关键代码
//求DFS序
void dfs(int x,int fa){
dfn[x]=++num;
rk[num]=x;
for(int i=h[x];i;i=e[i].nex){
int v=e[i].to;
if(v==fa){
continue;
}
dfs(v,x);
}
}
//线段树维护
void build(int k,int l,int r){
s[k].l=l;
s[k].r=r;
if(l==r){
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
s[k]=s[k<<1]+s[k<<1|1];
}
//修改
void change(int k,int x,int y,int z){
if(x<=s[k].l&&s[k].r<=y){
s[k].w=s[k].r-s[k].l;
s[k].ls=s[k].rs=s[k].lazy=z;
return;
}
pushdown(k);//warning 不要忘了下放懒标记
if(x<=s[k<<1].r){
change(k<<1,x,y,z);
}
if(y>=s[k<<1|1].l){
change(k<<1|1,x,y,z);
}
s[k]=s[k<<1]+s[k<<1|1];
}
//询问
tree query(int k,int x,int y){
if(x<=s[k].l&&s[k].r<=y){
return s[k];
}
pushdown(k);//warning 不要忘了下放懒标记
if(y<=s[k<<1].r){//如果区间全在左子树,就只在左子树上查找
return query(k<<1,x,y);
}
if(s[k<<1|1].l<=x){//同理
return query(k<<1|1,x,y);
}
return query(k<<1,x,y)+query(k<<1|1,x,y);
}
\(std\)
#树链剖分 #线段树
根据部分分2,线段树可以维护一条链,那么就自然的想到了把树变成链的算法树链剖分,树剖剖成多条重链用线段树进行维护。
时间复杂度 \(\mathcal{O}(T \cdot m\log^2_2 n)\)
\(Code\)
#include<bits/stdc++.h>
#define ls k<<1
#define rs k<<1|1
using namespace std;
inline long long read(){
long long x=0,w=0;char c=0;
while(c<'0'||c>'9') {w|=c=='-';c=getchar();}
while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();
return w?-x:x;
}
int n,m,x,y,z,t,cnt;
int son[100050],siz[100050],f[100050],dep[100050],dfn,id[100050],rk[100050],top[100050];
vector<int> mp[100050];
char op;
void dfs1(int x,int fa){
dep[x]=dep[fa]+1;
siz[x]=1;
f[x]=fa;
for(int i:mp[x]){
if(i==fa){
continue;
}
dfs1(i,x);
siz[x]+=siz[i];
if(siz[son[x]]<siz[i]){
son[x]=i;
}
}
}
void dfs2(int x,int root){
id[x]=++dfn;
rk[dfn]=x;
top[x]=root;
if(son[x]){
dfs2(son[x],root);
}
for(int i:mp[x]){
if(i==f[x]||i==son[x]){
continue;
}
dfs2(i,i);
}
}
//树链剖分
struct tree{
int l=0;
int r=0;
int lx=0;
int rx=0;
int lazy=0;
int w=0;
tree operator +(const tree&a)const{
tree res;
res.l=l;
res.r=a.r;
res.lx=lx;
res.rx=a.rx;
res.w=w+a.w;
if(rx==a.lx&&rx){
res.w++;
}
return res;
}
}s[500050];
void pushup(int k){
s[k]=s[ls]+s[rs];
}
void pushdown(int k){
if(!s[k].lazy){
return;
}
s[ls].lazy=s[ls].lx=s[ls].rx=s[rs].lazy=s[rs].lx=s[rs].rx=s[k].lazy;
s[ls].w=s[ls].r-s[ls].l;
s[rs].w=s[rs].r-s[rs].l;
s[k].lazy=0;
}
void build(int k,int l,int r){
s[k].l=l;
s[k].r=r;
if(s[k].l==s[k].r){
s[k].w=s[k].lazy=s[k].lx=s[k].rx=0;
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(k);
}
void change(int k,int x,int y,int c){
if(x<=s[k].l&&s[k].r<=y){
s[k].lx=s[k].rx=s[k].lazy=c;
s[k].w=s[k].r-s[k].l;
return;
}
pushdown(k);
if(x<=s[ls].r){
change(ls,x,y,c);
}
if(s[rs].l<=y){
change(rs,x,y,c);
}
pushup(k);
}
tree query(int k,int x,int y){
if(x<=s[k].l&&s[k].r<=y){
return s[k];
}
pushdown(k);
if(y<=s[ls].r){
return query(ls,x,y);
}
if(s[rs].l<=x){
return query(rs,x,y);
}
return query(ls,x,y)+query(rs,x,y);
}
//线段树维护
void solve1(){
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]<dep[fy]){
swap(x,y);
swap(fx,fy);
}
change(1,id[fx],id[x],z);
x=f[fx];
fx=top[x];
}
if(id[x]>id[y]){
swap(x,y);
}
change(1,id[x],id[y],z);
}
//修改
void solve2(){
int fx=top[x],fy=top[y];
tree ansx=(tree){0,0,0,0,0,0},ansy=(tree){0,0,0,0,0,0};
while(fx!=fy){
if(dep[fx]>dep[fy]){
ansx=query(1,id[fx],id[x])+ansx;
x=f[fx],fx=top[x];
}
else{
ansy=query(1,id[fy],id[y])+ansy;
y=f[fy],fy=top[y];
}
}
if(id[x]>id[y]){
ansx=query(1,id[y],id[x])+ansx;
}
else{
ansy=query(1,id[x],id[y])+ansy;
}
swap(ansx.lx,ansx.rx);
ansx=ansx+ansy;
printf("%d\n",ansx.w);
}
//查询
int main(){
t=read();
while(t--){
n=read();
m=read();
memset(son,0,sizeof(son));
memset(siz,0,sizeof(siz));
memset(f,0,sizeof(f));
for(int i=1;i<=n;i++){
mp[i].clear();
}
for(int i=1;i<n;i++){
x=read();
y=read();
mp[x].push_back(y);
mp[y].push_back(x);
}
dfn=0,cnt=0;
dfs1(1,0);
dfs2(1,1);
build(1,1,dfn);
for(int i=1;i<=m;i++){
cin>>op;
x=read();
y=read();
if(op=='1'){
z=++cnt;//时间戳变化
solve1();
}
else{
solve2();
}
}
}
return 0;
}
\(Warning\)
树链剖分的查询部分有一些难以理解和容易出错 (因为要注意合并的顺序) ,特此图解。
聚焦代码
void solve2(){
int fx=top[x],fy=top[y];
tree ansx=(tree){0,0,0,0,0,0},ansy=(tree){0,0,0,0,0,0};
while(fx!=fy){
if(dep[fx]>dep[fy]){
ansx=query(1,id[fx],id[x])+ansx;//聚焦点1
x=f[fx],fx=top[x];
}
else{
ansy=query(1,id[fy],id[y])+ansy;//聚焦点1
y=f[fy],fy=top[y];
}
}
if(id[x]>id[y]){
ansx=query(1,id[y],id[x])+ansx;//聚焦点1
}
else{
ansy=query(1,id[x],id[y])+ansy;//聚焦点1
}
swap(ansx.lx,ansx.rx);//聚焦点2
ansx=ansx+ansy;
printf("%d\n",ansx.w);
}
\(ansx \ 和 \ ansy \ 中只需注意转移 \ lx,rx,w \ 的值\)
图例
箭头表示跳跃的路程
加粗的点为重链的 \(top\)
数字为节点的时间戳
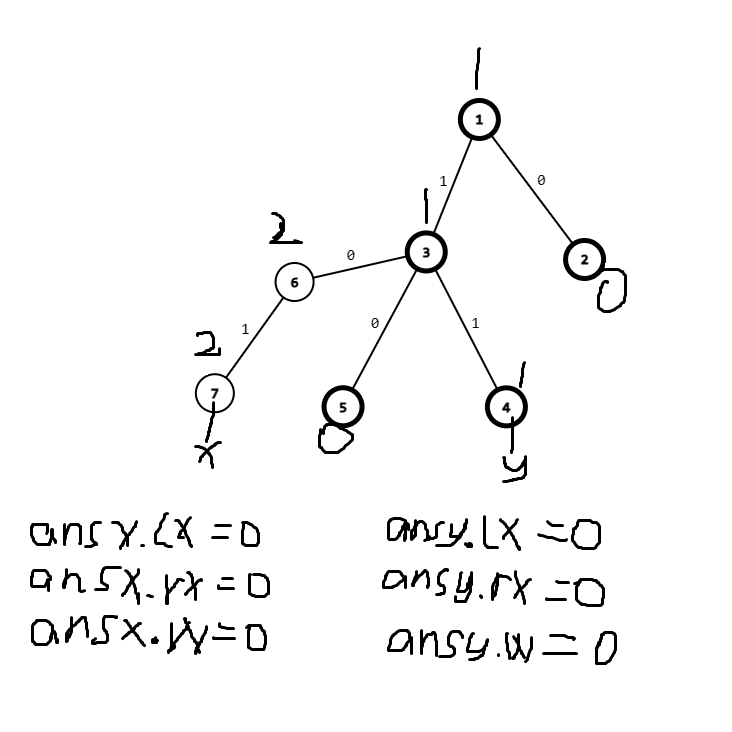
因为\(dep[fy]>dep[x]\)
所以
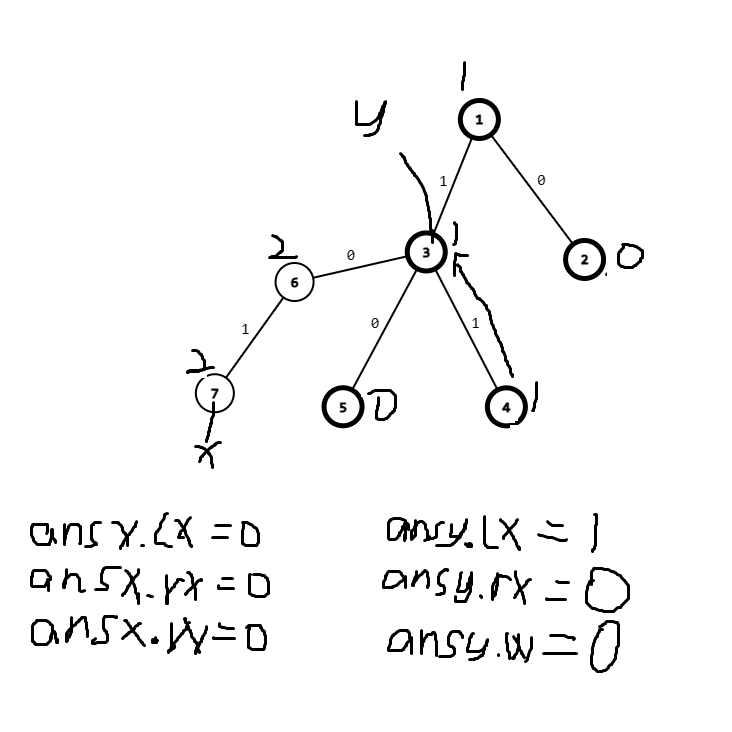
聚焦点1
因为\(id[x]>id[y]\)
所以
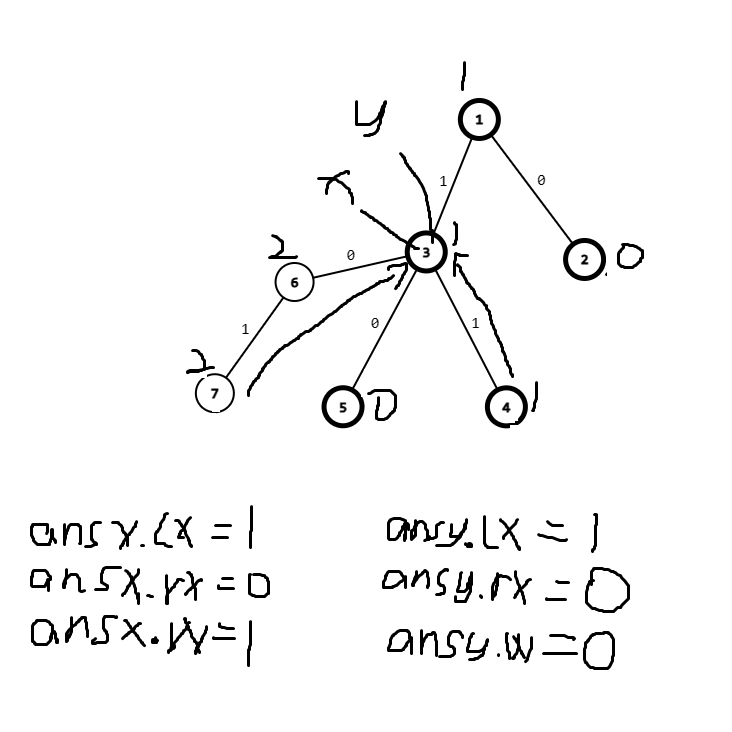
因为\(query()\)表示
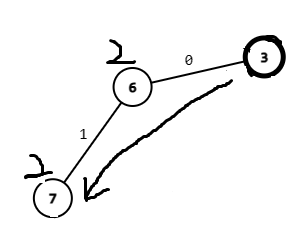
而\(x\)在\(7\)
\(ansx\)往上跳
所以为 \(ansx=query()+ansx\)
\(ansy同理\)
然后是最后的合并,\(x,y都在同一个节点上\)

聚焦点2
这时候我们发现, \(ansx.lx\) 表示的为 \(3\) 的时间戳,\(ansy.lx\)表示的为 \(4\) 的时间戳,而根据我们的合并。
tree operator +(const tree&a)const{//重载运算符,区间合并
tree res;
res.l=l;
res.lx=lx;//左儿子的左端点是区间左端点
res.r=a.r;
res.rx=a.rx;//右儿子的右端点是区间右端点
res.w=w+a.w;
if(rx==a.lx&&rx){//统计相邻点的答案 warning 当没有时间戳时不统计答案
res.w++;
}
return res;
}
应该是\(ansx.rx\)和\(ansy.lx\)表示相邻点的时间戳。
所以我们需要 \(swap(ansx.lx,ansx.rx)\)再进行 \(ansx=ansx+ansy\)