Problem Link

简要题意

题目很清楚。

分析

定理

两个人中左边的人一直向右运动，和两人向中间走所用的
步数相同

证明

假设有两组人为 \(a_l , a_r , b_l , b_r (a_l < a_r , b_l < b_r)\)。

\(\textrm{I}.\) 当 \(a_r < b_l\)（两者互不相交） 时

如图：

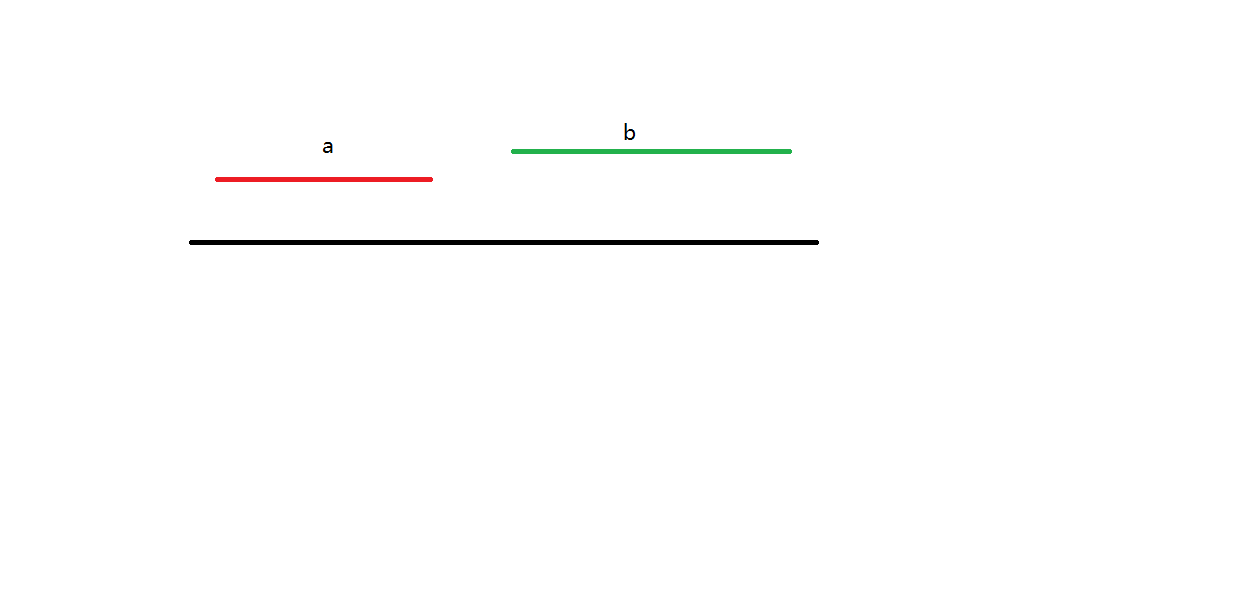
显然成立。

$ \textrm{II}.$ 当 $a_l < b_l < a_r < b_r $（两者相交） 时

如图：

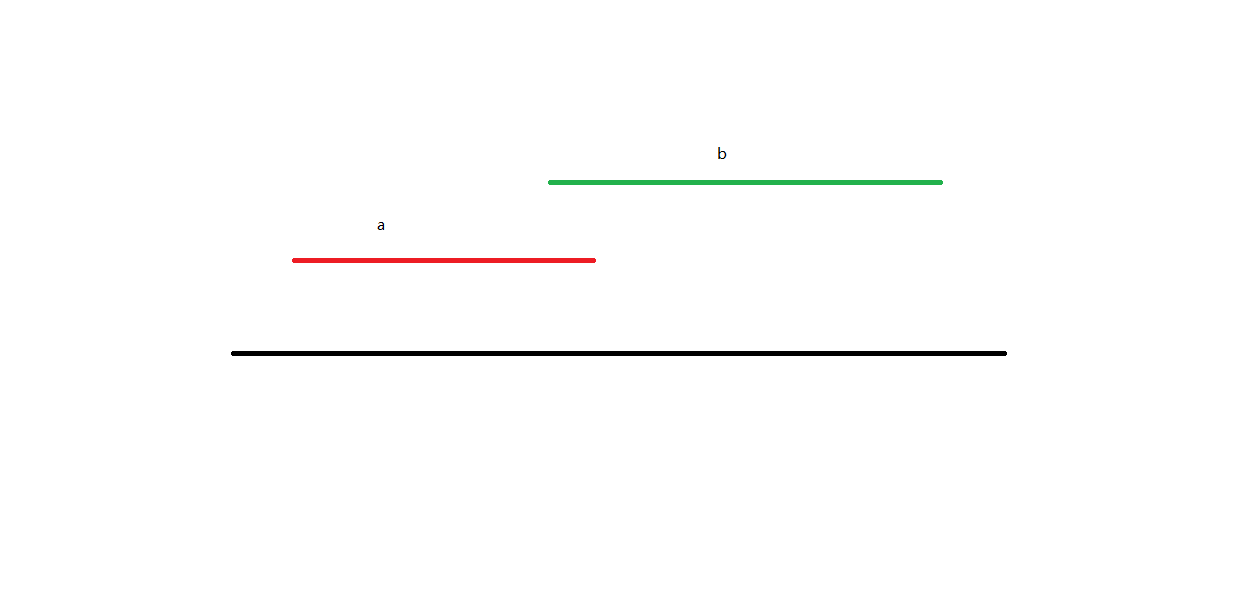
假设先走 \(a\)，此时 \(ans += a_r - a_l\)。

再走 \(b\)，此时 \(ans += b_r - b_l - 1\)（中间有一个 \(a_l\) 已经走完）。

最后 \(ans = (b_r - b_l) + (a_r - a_l) - 1\)。

再考虑将 \(a\) 两端走到 \(b\) 之间的情况（略，和上面的方法一样）。

$ \textrm{III}.$ 当 \(a_l < b_l < b_r < a_r\)（两者包含）时

略（并不难证和情况 \(2\) 证明方法一样）。

综上，证明得证。

此时题目就很简单了。

最终实现

那么就可以贪心的让区间短的先走就行了（因为先走小的，大的区间距离会减小；反之，则不行）。

那就只需要用树状数组记录其中的已消失的数，统计答案时减去区间已消失的数。

code

#include <bits/stdc++.h>

using namespace std;
using ll = long long ;

const int N = 5e5 + 5 ;

int n;

struct REN{
	int first,last;
	int len;
	bool operator<(const REN&x)const{return len<x.len;}	
}p[N];

ll ans;

struct FenwickTree{
	private:
		ll t[N<<1];
		int lowbit(int x){return x&-x;}
	public:
		void add(int x,int val){for(;x<=n*2;x+=lowbit(x))t[x]+=val;}
		ll ask(int x){ll ans=0;for(;x;x-=lowbit(x))ans+=t[x];return ans;}
}t;

int main(){
	scanf("%d",&n);
	for(int i=1,x;i<=2*n;i++){
		scanf("%d",&x);
		if(!p[x].first)p[x].first=i;
		else p[x].last=i;
		p[x].len=p[x].last-p[x].first; // 记录区间长度和头和尾
	}
	
	sort(p+1,p+n+1);//贪心
	
	for(int i=1;i<=n;i++){
		ans+=p[i].len-t.ask(p[i].last)+t.ask(p[i].first-1);//减去已经消失的
		t.add(p[i].first,1);
		t.add(p[i].last,1);// 记录这个人已经消失
	}
	printf("%lld",ans);
	return 0;
}