题意简述
给定一棵树,求断掉一条边再连上一条边所得的新树直径最小值和最大值,以及相应方案(你可以不进行任何操作,即断掉并连上同一条边)。
题目分析
假设我们枚举断掉某一条边,得到了两棵树,并且知道它们的直径分别为 \(d_0, d_1\),那么如何连接一条边让新树的直径最大 / 最小呢?
- 最大:显然,将两棵树的直径首尾相接,得到的直径是最大的,新树的直径长度是 \(d=d_0+d_1+1\)。别忘了新加的这条边的贡献 \(1\)。
- 最小:和 HXY 造公园 里的思想一样,我们将两个树的直径的中点相连(或者没有中点时取直径中心相邻的那两点任一),得到的新直径长度是 \(d = \max \lbrace d_0, d_1, \left \lceil \cfrac{d_0}{2} \right \rceil + \left \lceil \cfrac{d_1}{2} \right \rceil + 1 \rbrace\)。别忘了新加的这条边的贡献 \(1\)。
可是,我们这样只能知道答案直径的长度,以及断掉哪条边,那怎么知道断边之后连接哪两个点呢?如果在 \(\Theta(n)\) 枚举断边的同时把两棵树的直径求出来时间复杂度是 恐怖的 \(\Theta(n^2)\),显然超时。如何优化呢?事实上,我们完全不用每得到一个可能的答案就算出其具体方案,而是留到最后再处理,处理方法随便一个 \(\Theta(n)\) 求直径的方法都行。这样,总体的时间复杂度就是 \(\Theta(n)\) 的。于是,问题变成给出断开的边,如何求两颗树的直径长度。在这里提供了两种方法 \(\Theta(n)\) 地求解此题。
1. 树形 DP
钦定原树以 \(1\) 为根结点。枚举断边可以使用深搜,那么我们就需要在搜索的时候快速求得以 \(u\) 为根的子树的直径长度以及 \(fa[u]\) 这个方向上的直径长度。于是我们想到了使用树形 DP 求解。前者是树形 DP 求直径的模板,可以用一遍深搜预处理出来。考虑如何换根求得后者。在根从 \(fa[u]\) 变成 \(u\) 的时候,发现 \(fa[u]\) 这个方向上的树多出了 \(u\) 的兄弟子树,那么可能构成直径的分为以下几个部分。
- 原先 \(fa[fa[u]]\) 方向上的直径。
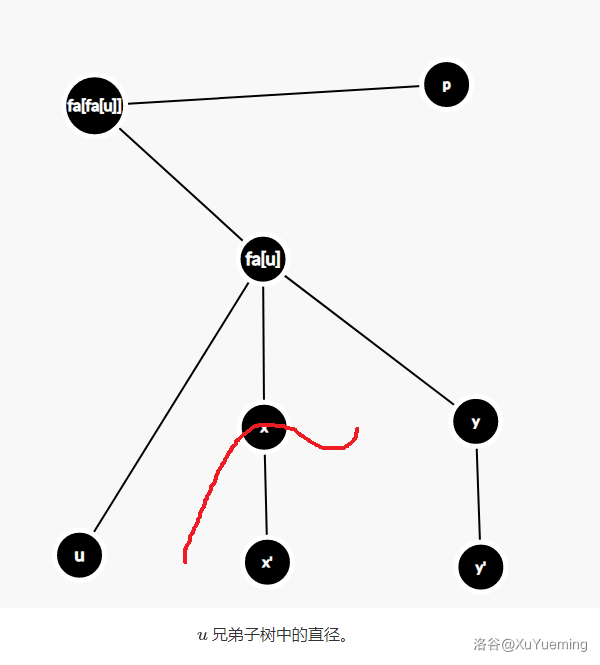
- \(u\) 兄弟子树中的直径。
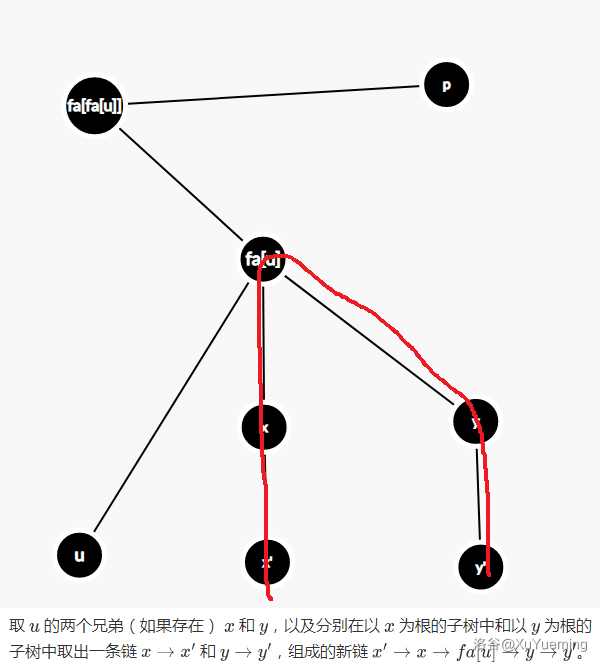
- 取 \(u\) 的两个兄弟(如果存在)\(x\) 和 \(y\),以及分别在以 \(x\) 为根的子树中和以 \(y\) 为根的子树中取出一条链 \(x \rightarrow x'\) 和 \(y \rightarrow y'\),组成的新链 \(x' \rightarrow x \rightarrow fa[u] \rightarrow y \rightarrow y'\)。
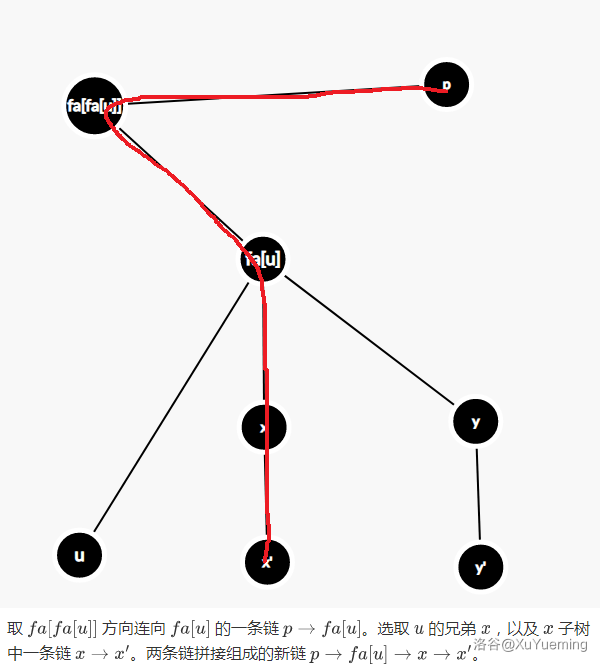
- 取 \(fa[fa[u]]\) 方向连向 \(fa[u]\) 的一条链 \(p \rightarrow fa[u]\)。选取 \(u\) 的兄弟 \(x\),以及 \(x\) 子树中一条链 \(x \rightarrow x'\)。两条链拼接组成的新链 \(p \rightarrow fa[u] \rightarrow x \rightarrow x'\)。
显然,以上分析囊括了不越过 \(fa[u]\) 和越过 \(fa[u]\) 的所有可能情况,不存在漏解。为了帮助理解,可以参考下图。

对于第二点,想到记 \(w_i\) 表示 \(i\) 所有子树中最长的直径,那么第二点直径长度就是 \(w_{fa[u]}\),但是请注意,我们要的是 \(u\) 的兄弟子树而不包括 \(u\) 这棵子树,万一 \(w_{fa[u]}\) 正好是 \(u\) 这棵子树中的直径就出现了问题。所以,套路化地,我们给 \(w\) 多加一维,变为 \(w_{i,0/1}\) 表示以 \(i\) 的所有子树中最长的直径 / 次长的直径。这样,对于上文提到的情况,就使用 \(w_{fa[u], 1}\) 来转移就没有问题。
对于第三种情况,想到记 \(d_{i, 0/1}\) 表示 \(i\) 所有子树中,根节点连出的最长链和次长链的长度。那么对于一般情况,合并后的直径长度就是 \(d_{fa[u],0}\) + \(d_{fa[u],1}\)。套路化地,发现当 \(u\) 这棵子树贡献了最长链或者次长链会产生问题,所以需要再开一维,记 \(d_{i,0/1/2}\) 表示 \(i\) 所有子树中,根节点连出的最长链、次长链和次次长链的长度。转移的时候注意不要使用到 \(u\) 这棵子树产生的信息就可以了。
对于第四种情况,我们需要知道 \(fa[u]\) 在 \(fa[fa[u]]\) 方向上最长链的长度,这个假设已经求得,为 \(chain_{fa[u]}\)。和 \(u\) 兄弟子树中根节点连出的最长链的长度,发现就是上文求的 \(d_{fa[u],0}\),当 \(u\) 这棵子树存在最长链的时候是 \(d_{fa[u],1}\)。那么合并后的直径长度就是 \(chain_{fa[u]} + d_{fa[u],0/1}\)。考虑如何使用信息更新 \(chain_u\)。首先,可能新的链是 \(chain_{fa[u]}\) 的基础上连上了 \(fa[u] \rightarrow u\) 这条边,长度是 \(chain_{fa[u]} + 1\)。其次可能是 \(u\) 兄弟子树连过来的一条边,长度是 \(d_{fa[u],0/1} + 1\),这个要根据 \(u\) 是否是最长链分类讨论。两者合并,得到 \(chain_u = \max\{chain_{fa[u]}+1,d_{fa[u],0/1}+1\}\)。
分析结束,具体使用代码实现就是两遍 DFS,第一遍预处理出 \(u\) 子树中直径长度 \(f_u\)、\(d_{u,0/1/2}\) 和 \(w_{u,0/1}\)。第二遍使用信息更新 \(fa[u]\) 方向上的直径 \(g_u\) 和 \(chain_u\),同时更新答案即可。具体实现和细节见代码。
2. 在原直径上 DP
假设在想到断掉一条边后,我们没有往树形 DP 的方向思考,而是想到了如下结论:
结论一:如果要获得直径的最小值,把原直径断开一定不劣。
证明:
设原树直径为 \(d\)。如果没有断开原直径,那么答案 \(D=\max \lbrace d,l,\left \lceil \cfrac{d}{2} \right \rceil + \left \lceil \cfrac{l}{2} \right \rceil + 1 \rbrace\) 一定有 \(D \geq d\),而我们断开连接同一条边获得的答案就是原树直径 \(d\) 显然不劣。所以为了得到更优的答案,就必须要把原树直径断开。
结论二:如果要获得直径的最大值,只可能是断开直径或者断开和直径连接的边
证明:
方案分为两种,即断开直径或者不断开直径。如果不断开直径,我们就需要和直径分离的那棵树直径最长,所以此时有删除和直径连接的这条边不劣。这是因为考虑直径上一个点 \(u\) 和与其相连的不在直径上的儿子 \(v\),如果断开的边在 \(v\) 这棵子树里,获得了一条直径,那么这条直径同样在断开连接 \(u\) 和 \(v\) 这条边后 \(v\) 的子树里,故删除和直径连接的这条边不劣
有了如上两个结论,实现方法呼之欲出。考虑先将原树直径“拉下来”,树的其他部分“挂”在这条直径上(详见下图),发现树上的问题变成了一个类似序列上的问题,简单了许多。从右向左遍历直径上相邻的点对 \((u, v)\),删除他们之间的边,快速求得 \(u\) 这边和 \(v\) 这边树的直径,然后统计答案。对于断开和直径相连的边,暴力枚举时间复杂度不超过 \(\Theta(n)\),问题就得到解决。
接下来考虑从右向左枚举断边从 \((v,y)\) 变为 \((u,v)\) 的过程,两树直径变化。首先对于左树的直径我们可以预处理出来,那么只需要考虑多出的 \(y\) 以及它的不在直径上的子树对右半部分直径产生的贡献,和前文树形 DP 讨论方法类似,分为不经过 \(y\) 和经过 \(y\) 的直径,具体如下:
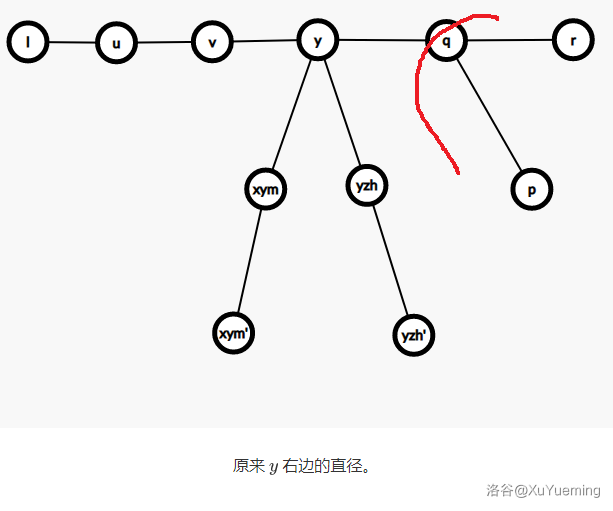
- 原来 \(y\) 右边的直径。
- 以 \(y\) 为根的不经过原树直径的直径。
- 对于 \(y\) 一个儿子 \(yzh\) 和它子树里以 \(yzh\) 为一个端点的链 \(yzh \rightarrow yzh'\),以及 \(y\) 右边延伸过来的一条链 \(p \rightarrow y\) 组成的直径 \(yzh' \rightarrow yzh \rightarrow y \rightarrow p\)。
可以借助下图进行形象地理解。
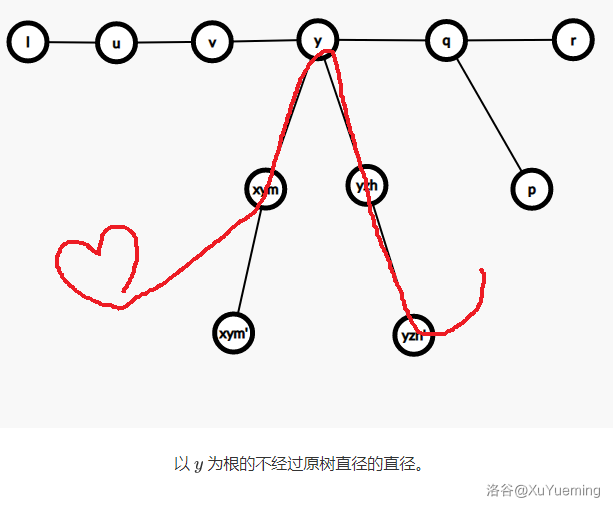

对于第二点,发现可以和求左树直径一样用同一个 DFS 预处理出来。
对于第三点,我们只用记 \(y\) 连出的不经过原直径最长链的长度 \(f_y\),和右边伸过来的链 \(R_{len}\) 和并得 \(f_y+R_{len}\)(你看看次长、次次长都不见了)。那么,我们怎么算得对于 \(v\) 的 \(R_{len}'\) 呢?发现可以是目前链再向左延伸或者是 \(y\) 中一条长链连过来,故 \(R_{len}'=\max \lbrace R_{len}+1,f_y+1 \rbrace\)。
分析结束,完成了对本题的求解。具体使用一遍深搜把原树直径“拉下来”再反着枚举断边,同时更新 \(R_len\)。随后枚举断于直径相连的边。最后分别求出答案要求的连接哪些边。具体实现和细节见代码。
代码及具体实现(已略去快读快写,码风清新,注释详尽)
1. 树形 DP 目前最优解 rank3
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in","r",stdin), freopen(#a".out","w",stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
struct node{
int to, nxt;
} edge[500010 << 1];
int eid, head[500010];
void add(int u, int v){
edge[++eid] = node({v, head[u]});
head[u] = eid;
}
int n;
int kmin = 0x3f3f3f3f, x1min, y1min, x2min, y2min;
int kmax = -0x3f3f3f3f, x1max, y1max, x2max, y2max;
// f[i] 表示以 i 为子树的直径长度
// d[i][0/1/2] 表示表示 i 向其子树连出的最长链、次长链、次次长链的长度
// w[i][0/1] 表示 i 所有子树中的最长直径(也就是不跨过 i 的最长直径)
// chain[i] 表示 fa[i] 方向连过来的最长链的长度
int f[500010], d[500010][3], w[500010][2], chain[500010];
void Dfs(int now, int fa){
for (int i = head[now]; i; i = edge[i].nxt){
int to = edge[i].to;
if (to == fa) continue;
Dfs(to, now);
f[now] = max<int, int, int>(f[now], f[to], d[now][0] + d[to][0] + 1);
// 树形 DP 求直径
if (d[to][0] + 1 > d[now][0]) d[now][2] = d[now][1], d[now][1] = d[now][0], d[now][0] = d[to][0] + 1;
else if (d[to][0] + 1 > d[now][1]) d[now][2] = d[now][1], d[now][1] = d[to][0] + 1;
else if (d[to][0] + 1 > d[now][2]) d[now][2] = d[to][0] + 1;
// d[to][0] + 1 就是 now 向 to 连出的最长链的长度,用其更新 now 的最长链、次长链、次次长链的长度
// 如果有两条相同的最长链,我们把一个看做次长链,就避免了冗长的分类讨论
if (f[to] > w[now][0]) w[now][1] = w[now][0], w[now][0] = f[to];
else if (f[to] > w[now][1]) w[now][1] = f[to];
// 更新 i 所有子树中的最长直径
}
}
int g[500010];
void redfs(int now, int fa){
if (fa != 0){
// 不是根节点就尝试断开 now 和 fa 之间的边
if (kmax < g[now] + f[now] + 1) kmax = g[now] + f[now] + 1, x1max = fa, y1max = now;
// 求最长直径
int len = max<int, int, int>(f[now], g[now], (f[now] + 1) / 2 + (g[now] + 1) / 2 + 1);
if (kmin > len) kmin = len, x1min = fa, y1min = now;
// 求最短直径
}
for (int i = head[now]; i; i = edge[i].nxt){
int to = edge[i].to;
if (to == fa) continue;
chain[to] = chain[now] + 1; // 新的链是 fa[now] -> now 的基础上连上了 now -> to
g[to] = g[now]; // 对应第一种情况
if (d[to][0] + 1 == d[now][0]){
g[to] = max<int, int, int>(g[to], chain[now] + d[now][1], d[now][1] + d[now][2]);
chain[to] = max(chain[to], d[now][1] + 1);
} else if (d[to][0] + 1 == d[now][1]){
g[to] = max<int, int, int>(g[to], chain[now] + d[now][0], d[now][0] + d[now][2]);
chain[to] = max(chain[to], d[now][0] + 1);
} else {
g[to] = max<int, int, int>(g[to], chain[now] + d[now][0], d[now][0] + d[now][1]);
chain[to] = max(chain[to], d[now][0] + 1);
}
// 判断链长是不是最长链,次长链、次次长链,可以画图辅助理解
if (f[to] == w[now][0]) g[to] = max(g[to], w[now][1]);
else g[to] = max(g[to], w[now][0]);
// 对应第二种情况
redfs(to, now);
}
}
int pre[500010], dis[500010], mxpos;
void dfs(int now, int fa, int skip = -1){
if (dis[now] > dis[mxpos]) mxpos = now;
for (int i = head[now]; i; i = edge[i].nxt){
int to = edge[i].to;
if (to != fa && to != skip){
dis[to] = dis[now] + 1, pre[to] = now;
dfs(to, now, skip);
}
}
}
int Diameter[500010], Dlen;
bool InDiameter[500010];
void GetDiameter(int u = 1, int v = -1){
int p = -1, now = -1;
mxpos = u, dis[u] = 0, pre[u] = -1, dfs(u, 0, v), p = mxpos;
mxpos = p, dis[p] = 0, pre[p] = -1, dfs(p, 0, v), now = mxpos;
for (int i = 1; i <= n; ++i) InDiameter[i] = false;
for (Dlen = 0; ~now; InDiameter[now] = true, Diameter[++Dlen] = now, now = pre[now]);
}
// 搜直径并把直径“拉下来”
int GetNodeOfDiameter(int u = 1, int v = -1){
return mxpos = u, dis[u] = 0, pre[u] = -1, dfs(u, 0, v), mxpos;
}
// 获取直径的一端
signed main(){
read(n);
for (int i = 1, u, v; i <= n - 1; ++i) read(u, v), add(u, v), add(v, u);
Dfs(1, 0), redfs(1, 0);
GetDiameter(x1min, y1min), x2min = Diameter[(Dlen + 1) / 2];
GetDiameter(y1min, x1min), y2min = Diameter[(Dlen + 1) / 2];
x2max = GetNodeOfDiameter(x1max, y1max);
y2max = GetNodeOfDiameter(y1max, x1max);
write(kmin, ' ', x1min, ' ', y1min, ' ', x2min, ' ', y2min, '\n');
write(kmax, ' ', x1max, ' ', y1max, ' ', x2max, ' ', y2max, '\n');
return 0;
}
2. 在原直径上 DP 目前最优解 rank1
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in","r",stdin), freopen(#a".out","w",stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
struct node{
int to, nxt;
} edge[500010 << 1];
int eid, head[500010];
void add(int u, int v){
edge[++eid] = node({v, head[u]});
head[u] = eid;
}
int n;
int kmin = 0x3f3f3f3f, x1min, y1min, x2min, y2min;
int kmax = -0x3f3f3f3f, x1max, y1max, x2max, y2max;
int pre[500010], dis[500010], mxpos;
void dfs(int now, int fa, int skip = -1){
if (dis[now] > dis[mxpos]) mxpos = now;
for (int i = head[now]; i; i = edge[i].nxt){
int to = edge[i].to;
if (to != fa && to != skip){
dis[to] = dis[now] + 1, pre[to] = now;
dfs(to, now, skip);
}
}
}
int Diameter[500010], Dlen;
bool InDiameter[500010];
void GetDiameter(int u = 1, int v = -1){
int p = -1, now = -1;
mxpos = u, dis[u] = 0, pre[u] = -1, dfs(u, 0, v), p = mxpos;
mxpos = p, dis[p] = 0, pre[p] = -1, dfs(p, 0, v), now = mxpos;
for (int i = 1; i <= n; ++i) InDiameter[i] = false;
for (Dlen = 0; ~now; InDiameter[now] = true, Diameter[++Dlen] = now, now = pre[now]);
}
// 搜直径并把直径“拉下来”
int GetNodeOfDiameter(int u = 1, int v = -1){
return mxpos = u, dis[u] = 0, pre[u] = -1, dfs(u, 0, v), mxpos;
}
// 获取直径的一端
// f[i] 表示 i 向非直径连出的最长链长度
// g[i] 表示 i 子树的直径
int f[500010], g[500010];
void TreeDP(int now, int fa){
for (int i = head[now]; i; i = edge[i].nxt){
int to = edge[i].to;
if (to != fa){
TreeDP(to, now);
if (InDiameter[to]) continue; // 这句话很巧妙地做到了分别以直径上的每个结点往直径外搜索
g[now] = max<int, int, int>(g[now], g[to], f[to] + 1 + f[now]);
f[now] = max(f[now], f[to] + 1);
// 说明 to 不是直径上的结点,更新最长链和直径
}
}
}
int p[500010];
signed main(){
read(n);
for (int i = 1, u, v; i <= n - 1; ++i) read(u, v), add(u, v), add(v, u);
GetDiameter(), TreeDP(Diameter[1], 0);
// 先把直径拉下来
for (int i = 1, now = 0; i <= Dlen; ++i){
// 这里 i 表示把直径拉下来后第 i 个直径结点
// 正着扫,p[i] 表示前缀直径
// 考虑新增部分的贡献,可能直径完整在 i 的的子树里,即 g[Diameter[i]]
// 也可能是之前连向 i 的最长链和 i 向子树连出的最长链
p[i] = max<int, int, int>(p[i - 1], g[Diameter[i]], now + f[Diameter[i]]);
// 这里的 now 就是维护连到 i 的最长链的长度
// 可能是之前那条链再向右延伸,或者是从 i 的子树里连过来
now = max(now + 1, f[Diameter[i]] + 1);
}
// 接下来倒着扫一遍,尝试删除直径上 i - 1 号点和第 i 号点之间的边
// 同样用 Rlen 记录右半部分的直径长度
// 用 now 记录从右边连向 i 的最长链的长度
for (int i = Dlen, Rlen = 0, now = 0; i - 1 >= 1; --i){
Rlen = max<int, int, int>(Rlen, g[Diameter[i]], now + f[Diameter[i]]);
now = max(now + 1, f[Diameter[i]] + 1);
// 同前面的维护
int len = max<int, int, int>(p[i - 1], Rlen, (Rlen + 1) / 2 + (p[i - 1] + 1) / 2 + 1);
if (len < kmin) kmin = len, x1min = Diameter[i], y1min = Diameter[i - 1];
// 维护最小直径
if (Rlen + 1 + p[i - 1] > kmax) kmax = Rlen + 1 + p[i - 1], x1max = Diameter[i], y1max = Diameter[i - 1];
// 维护最长直径
}
// 为了获得最长直径,我们还要把和直径相连的边都尝试断一遍
// 这里直接枚举直径上的点,在枚举它连出的边
for (int i = 1; i <= Dlen; ++i) for (int j = head[Diameter[i]]; j; j = edge[j].nxt){
int to = edge[j].to;
if (!InDiameter[to]){
// 更新最长直径
if (Dlen + g[to] > kmax) kmax = Dlen + g[to], x1max = Diameter[i], y1max = to;
}
}
// 最后求得具体方案
GetDiameter(x1min, y1min), x2min = Diameter[(Dlen + 1) / 2];
GetDiameter(y1min, x1min), y2min = Diameter[(Dlen + 1) / 2];
x2max = GetNodeOfDiameter(x1max, y1max);
y2max = GetNodeOfDiameter(y1max, x1max);
write(kmin, ' ', x1min, ' ', y1min, ' ', x2min, ' ', y2min, '\n');
write(kmax, ' ', x1max, ' ', y1max, ' ', x2max, ' ', y2max, '\n');
return 0;
}