图论学习总结 2
拓补排序
当给定的一张图是一张 DAG(有向无环图)时,可以对该图进行拓补排序,在 \(O(n+m)\) 的时间内转移一些信息。通常用队列进行实现。拓补排序经常与其他算法进行结合,如 DP。
例题
[POI2015] PUS (Pustynia)
当一些数之间只给定了大小关系,要求一组可行解时,可以考虑使用拓补排序求解。考虑用较小的数往较大的数连边,由于我们想让一个数在满足限制的条件下尽可能的小,所以它的值可以定为比它小的数中的最大值加 1。若存在 \(a_i < a_j < a_k < \cdots < a_i\),显然无解,而此时这些数转换到图上构成一个环,因此只要图中有环就无解。对于开始已经给定值的数,让其点权先等于给定值,若跑完拓补排序后与原值不同也无解。
如果存在值相同的情况,可以把相同的值放到一个并查集里,看作一个点,统一限制。
【HNOI2015】落忆枫音
先考虑没有环的情况情况怎么做,答案显然为 \(\prod\limits_{i=2}^{n} d_i\),其中 \(d_i\) 为节点 \(i\) 的入度,相当于给每个节点(1 除外)钦定一个父节点。
现在考虑有环的情况。由于正着不好做。所以考虑还是用原来的方式求。设加入新边之后点 \(i\) 的入度为 \(d_i'\),则当前算出的答案为 \(\prod\limits_{i=2}^{n} d_i'\)。但是由于会把环的方案算进去,所以考虑把包含环的方案减去。本来我以为添加一条边最多产生一个环,然而有很显然的反例。
不加边之前:
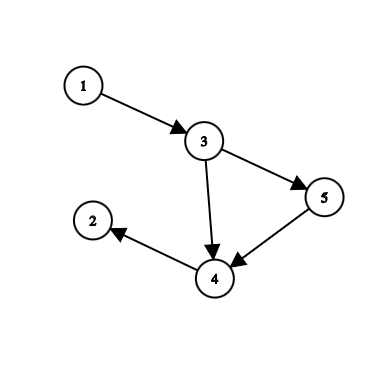
加入边 \((2,3)\) 后:
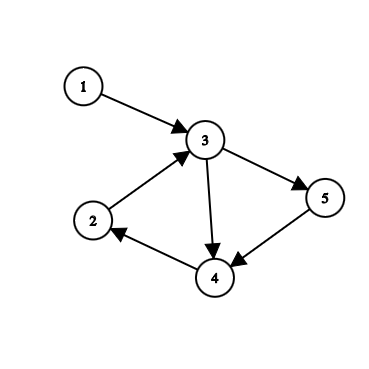
这明显已经产生了多个环,所以不能考虑将环一个个找出。由于原图是 DAG,所以不管在原图上选出哪些边都不会形成环,因此增加的环在删去 \((s,t)\) 这条边后一定是一条 \(t \to s\) 的一条路径,只需统计 \(t \to s\) 的路径方案数即可。考虑使用动态规划,设 \(f_i\) 表示在原图上从 \(t \to i\) 的路径方案数,方程即为:
\[f_v = \sum\limits_{u \to v} \frac{f_u}{d_v} \]相当于原来可能有多个父亲,但是我只钦定一个。最后把按照原来方式算出的方案数减去 \(f_s\) 即可。
[CSP-S 2020]函数调用
本来我想的是把对一个函数的调用堆积到最后一起计算,但是搞了半天也不会。由于乘法操作是一次把所有数都乘以一个系数,所以最后可以对原值直接操作。现在的棘手问题是加法操作的对象是唯一的,所以加权的系数需要分别计算。由于先前的加法操作在给其对应位置加值后,后续的乘法操作会将其加权的系数扩倍,所以可以将其先后顺序颠倒一下,方便计算。设 \(f_i\) 表示调用函数 \(i\) 会使其后继加法函数的系数,方程即为:
\[f_v = \sum\limits_{u \to v} f_u \cdot p \]这里的 \(p\) 是比 \(v\) 的优先级低的函数对乘法操作的系数贡献累乘,而对于该函数内的乘法系数贡献可以进了下一个函数再细分。对于最后的一堆函数调用,我偷了个懒,直接新建了一个超级源点,按顺序连向这些函数,并使 \(f_s = 1\),这样可以避免一些冗余的操作。
二分图
二分图的判定
染色法,将与自己相邻的点染成不同颜色,如果矛盾则不是二分图。
例题
双栈排序
看到“双”栈,而且还看到要判定无解,很容易想到用染色法判定二分图。考虑如何建模。
根据二分图染色的过程,相邻的点与自己颜色不同,所以图中的边连接了两个属于不同栈的节点。考虑 \(i,j(i<j)\) 在何时才必须不在同一栈内。显然只有这两个数是不行的,因为只看这两个数是一定有方案使它们在同一个栈的。只有当 \(\exist k>j\) 且 \(a_k < a_i < a_j\) 时,\(i\) 和 \(j\) 才必须不在同一栈内,因为由于大小关系 \(i\) 必须在 \(j\) 前出栈,而位置关系又决定了 \(k\) 在 \(i\) 之后出栈,这样就是降序排列,不符合。这就是染色法判定二分图。
在染色后就可以得到每个元素归属于哪个栈。由于要求字典序最小,所以考虑贪心,在入栈 \(1\) 时先弹栈 \(1\),在必须弹栈 \(2\) 时再弹,之后入栈。在入栈 \(2\) 时,先把栈 \(1\) 能弹的都弹了,再弹栈 \(2\),最后入栈。
欧拉路径
此知识点最难的就是:看出一道题与欧拉路径相关;有欧拉路径进行建模。
例题
POLICE
思路太妙了,实在是佩服能想出来的人。
先考虑所有书都在原书架的情况。由于要尽可能的少用操作 \(2\),就要多用操作 \(1\)。在保证一定有空位的情况下,我们可以用操作 \(1\) 完成多次挪动。可以将原书架上的书位置与现书架上的书位置做一个映射,容易发现满足了位置靠后的映射就不能再满足靠前的映射了。所以不用操作 \(2\) 的最大操作 \(1\) 次数即为映射后的 LIS 长度,需要的操作 \(2\) 次数就是书的本数减去 LIS 的长度。
接下来考虑一般情况。对于在其原来书架上的书,我们还是按上述方法,这样可以减少操作 \(2\) 的使用。对于必须与其它行的书交换的,我们把一次交换抽象成一条有向边。显然,我们至少需要使用边数次操作 \(2\) 才能使得所有书归位,但实际上我们也 仅需使用边数次操作 \(2\)。考虑选出一个入度大于出度的点连向一个出度大于入度的点,一直连边,直到所有点的入度都等于出度。可以发现,连完边的图 __存在欧拉回路,在欧拉回路上,每条边都恰好对应了一次交换,而且这些交换可以通过合理安排顺序使得所有书归位。__这样就证明了只需使用边数次操作 \(2\)。需要注意的是,如果当前联通块中如果没有空位的话,我们还需要一次额外操作,将空位交换到这个联通块中。
这道题确实很难想到与欧拉回路有关。
宝石装箱
可以发现把宝石或着价值作为点,都无法很好的处理限制,所以考虑以颜色作为点,把在相同箱子的连一条边。
先满足第一个条件,发现和等差数列很类似,直接用宝石 \(i\) 的颜色向宝石 \(4n - i + 1\) 的颜色连边,这样保证了所有的边上端点点权和为 \(4n + 1\)。之后显然可以发现,图上所有点的度都为 \(4\),所以必定存在欧拉回路。把欧拉回路跑出来后,我们只需要 间隔的选边,就可以满足第二个限制,因为每条边向两个端点都贡献了一个度。
[省选联考 2020 B 卷] 丁香之路
发现其实就是求一条 \(s \to i\) 的欧拉通路,只不过是每条边至少经过一次。
我们先把 \(m\) 条边加入答案边集中,方便处理。由于欧拉通路不太好处理,考虑转换成欧拉回路,由于 \(s\) 和 \(i\) 是端点,所以将 \(s\) 与 \(i\) 连边即可。现在考虑将边集变为欧拉回路,实质上就是将奇度数的点相互连边。考虑将相邻的奇度数点连边,这样可以保证最优,因为相邻点连边一定优于跳跃连边。但是还有一个问题就是 图不一定连通。由于联通块内已经连通,所以只需要考虑在联通块之间连边。还是套用刚刚的方法,将相邻且不在同一联通块内的点连边,依旧可以保证最优,因为跳跃连边不优。可以发现,用最小的代价将图联通就是最小生成树,所以跑一个 Kruscal 即可。注意,将图联通时,由于要保证所有点的度数为偶,所以要连两条边。
最小生成树
最小生成树常与其他知识点结合,如倍增、树剖、线段树等。
例题
跨越雷区
发现左右边界没有什么用。显然,答案具有二分性,因为大的答案都满足了,小的也能满足,所以考虑二分答案。每个点所管辖的区域都是一个以其为圆心,半径为二分值的一个圆,如果两个圆有交(圆心距离小于二倍半径),则它们中间的区域不能通过,我们可以用一个并查集维护,将这两个点所在并查集合并,再建两个虚点,分别代表上界与下界,再用相似方法连边,最后若上界和下界联通,则说明路被堵死,无法通过。但是由于数据过于毒瘤,无法通过。
考虑二分的过程,发现实际上就是逐渐尝试扩大半径,等到上下界联通后就停止。这其实就是最小生成树,将其跑出后,最小生成树上的最大边就是满足条件的最大圆心距离,将其除以 \(2\) 就是答案。
但是如果用 Kruscal 求解的话,时间复杂度还是带一个 \(\log\),依旧超时。考虑到图是一张完全图,所以可以用 Prim 算法求解,时间复杂度 \(O(k^2)\),可以通过。
水壶
考虑贪心的思想:能走建筑物就走建筑物,这样可以保证最大值最小。
先跑一遍多源最短路,并记录最短路从哪个点转移过来。如果两条最短路相遇,且两条路径起点不同,就将这两个路径起点相连,这样可以保证两个点之间的最大边权相对较小。然后再用 Kruscal 重构树,将环上不必要的大边去掉,最后答案即为 \(u\) 到 \(v\) 的路径上的最大边权。
强连通分量(SCC)
主要技术就是缩点,缩点之后是一张 DAG,可以在上面跑拓补,然后和 DP 等算法配合。
例题
狼人游戏
可以发现,在一个 SCC 中,只要问一个点,就可以知道所有点的情况。所以先把图缩点,然后发现知道了一个 SCC 的情况后,它的后继节点也可以知道了,所以只有入度为 \(0\) 的 SCC 是需要进行询问的,做一个统计。但是这样有一个问题,假设有四个人,我已经知道了 \(1,2,3\) 都不是狼人,那 \(4\) 就一定是狼人。所以要特别考虑一种情况:如果一个 SCC 中只有一个点,且它的后继节点不一定非要它才能被了解(即入度大于 \(1\)),那么就可以不用询问它。注意,如果有多个这样的点,最多只能不问其中一个。
最后的答案计算,假设总共需要问 \(k\) 次,问第 \(1\) 次存活下来的概率为 \(\frac{n-1}{n}\)。问第二次时,虽然有些点已经知道,可以不用再问,但是我们也可以去问,反正存活率 \(100 \%\),不影响,所以问第 \(2\) 次存活下来的概率为 \(\frac{n-2}{n-1}\),第三次为 \(\frac{n-3}{n-2}\),\(\cdots\),第 \(k\) 次为 \(\frac{n-k}{n-k+1}\)。最后答案即为:
\[\frac{n-1}{n} \cdot \frac{n-2}{n-1} \cdot \thinspace \cdots \thinspace \cdot \frac{n-k}{n-k+1} = \frac{n-k}{n} \]交通网络
本来以为能访问的区间不是一段连续的,那这么做就会超时。但是由于 图是一张平面图,所以有一个很重要的性质:一个左部点能到达的右部点按照 \(y\) 坐标排序后一定是一段连续区间(除开不能被任何左部点到达的右部点)。这样就可以直接先缩点(一个 SCC 中的点可以相互到达),然后通过拓补合并一个点能到达的最小左端点和最大右端点,最后求出该区间内有多少能被左部点到达的右部点即可,可以使用前缀和。
双连通分量(DCC)
双连通分量有一个很好的性质:缩点之后是一棵树。边双的缩点与强连通分量类似,这里主要介绍点双缩点:Block-Cut Tree。
Block-Cut Tree
由于一个割点可能存在于多个点双中,所以不能简单的把点双缩成一个点。但是我们可以考虑 把点双中不是割点的点缩成一个点,然后再和点双中的割点连边。
如下图,原图为:
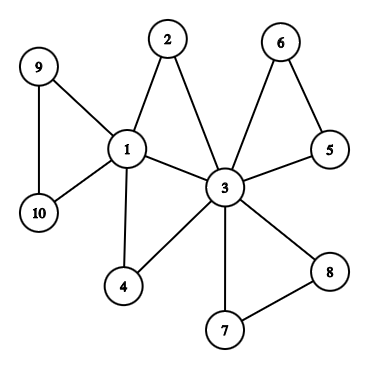
进行缩点(每个点双中,非割点的点缩点后选择一个原来的点编号作为新编号)后:
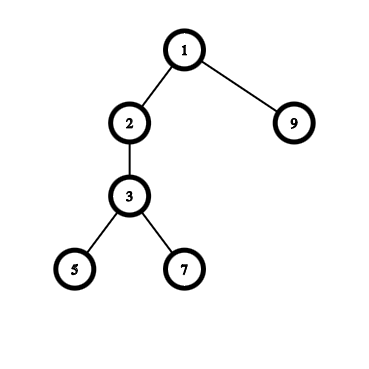
这样,图就变成了一棵树,可以进行一些方便的操作。
例题
[AHOI2005] LANE 航线规划
正着做显然不好做,考虑向并查集一样,把正删边改为倒加边。由于边双内的边和点都不会产生贡献,所以将边双缩点,之后就能得到一棵树。考虑加边,树上在加了一条边后,会且仅会产生一个环,而环上的边(即在两点路径上的边)都不会再是割边,贡献从 \(1\) 变为 \(0\)。相当于我们要进行链修改,链查询,可以考虑用树剖维护,时间复杂度为 \(O(n \log^2 n)\)。也可以考虑用树状数组加并查集维护,时间复杂度为 \(O(n \log n)\),更优秀。
「CEOI2017」One-Way Streets
一个很显然的性质:边双中的边不用定向,因为边双中两点间有至少两条边不重复的路径,所以有多条可行路径,没有必须经过的边。所以将边双缩点,得到一棵树。从树根开始对树进行遍历,实质上就已经根据点的访问顺序将树边定向。接下来,考虑将从 \(u\) 到 \(v\) 路径上经过的割边定向,先求出 \(u,v\) 分别所在的边双编号 \(u',v'\),结合跳 \(LCA\) 的过程,从 \(u'\) 到 \(LCA\) 上的树边与遍历树时的方向相反,而从 \(LCA\) 到 \(v'\) 上的树边与遍历树时的方向一致,考虑用倍增进行打标记即可。
小结
图论,实际上最难的一般不是在图上求解问题,而是 找出题目与图的关系,将元素之间的关系抽象成图,将原问题转化为图上的等价问题进行求解。所以,多数图论题难就难在建模,如欧拉路径相关题目,需要勤加练习才能总结出一些经验,同时也需要灵活的思维才能找到联系。
标签:总结,连边,图论,所以,可以,路径,冯梓轩,考虑,欧拉 From: https://www.cnblogs.com/gevenfeng/p/18005956