首页 > 其他分享 >数论1-素数

数论1-素数

时间：2024-01-29 19:57:43浏览次数：31  
标签：frac 数论 质数 int 素数 pmod equiv

Part 1 前置

记号约定

  • 整数集合 ：$ \Z ={...,-2,-1,0,1,2,…}$

  • 自然数集合：\(\N=\{0,1,2,…\}\), 下文若不特殊说明，则出现的所有字母皆代表自然数。

  • 整除：若 \(a=b\times k\), 则 \(b\) 整除 \(a\), 记作 \(b \mid a\), 否则记作 \(b \nmid a\)

  • 约数：若 \(b\mid a\) 且 \(b\ge 0\),则称 \(b\) 是 \(a\) 的约数，\(a\) 是 \(b\) 的倍数。约数有一些性质，这里按下不表。

  • 因子：\(a\) 除了 \(1\) 和 \(a\) 本身以外的所有约数称为 \(a\) 的因子。（这里为了方便，就直接这么写了）

何为数论

研究整数性质的数学分支，本质上是对质数（素数）的研究。

Part 2: 素数的一切

若不加额外说明，下文中 \(p\) 皆表示质数，\(m\) 表示非质数且 \(m>1\)。

定义

  • 素数（质数）：\(p>1\) 且没有因子的数。
  • 合数：\(m>1\) 且有因子的数。
  • 其他整数（0,1）既不是质数也不是合数。
    • 素数的分布规律：不大于 \(n\) 的素数约有 \(\frac{n}{\ln{n}}\) 个。

判断

#1

若 \(m\) 不是质数，则它一定有至少一个素因子，这些素因子一定不会大于 \(\sqrt{m}\) 。

那么只要从 \(2\) 枚举到 \(\sqrt{m}\) 判断能否整除即可。

时间复杂度单次 \(\mathcal O(\sqrt{m})\)。

Code:

bool isprime(int m){
    if(m<2)return false;
    for(int i=2;i*i<=m;i++)
        if(m%i==0)return false;
   	return true;
}

#2 \(kn+i\) 法

最近学到的一个黑科技。我们枚举时并不需要把所有数都看一遍。\(m\) 如果不是质数，那么它一定有素因子。我们枚举时只需要枚举可能为素因子的数即可。

比如当 \(k=6\) 时，我们只需要枚举 \(kn+1\) 和 \(kn+5\) 即可，其他数不可能为质数。

时间复杂度仍为单次 \(\mathcal O(\sqrt{m})\)，但是常数小了好多。

Code:(此处 \(k=30\))

bool isprime(int m){
    if(m==2||m==3||m==5)return true;
    if(m%2==0||m%3==0||m%5==0||m==1)return 0;
    int c=7,a[8]={4,2,4,2,4,6,2,6};
    while(c*c<n){
        for(auto i:a){
            if(n%c==0)return 0;
        	c+=i;
        }
    }
    return 1;
}

#3 预处理

对于多组数据，每个 \(m\) 必然有小于等于 \(\sqrt{m}\) 的素因子，只需要对 \(\sqrt{m}\) 内的素数测试即可。

我们可以预处理出 \(\sqrt{m}\) 内的素数，再让每一个 \(m\) 对这些素数进行测试。

时间复杂度近似 单次 \(\mathcal O(\frac{m}{\ln{m}})\)。

预处理详见下章，代码不贴了。

#4 Miller_Rabin

最重要。

前置知识-费马小定理

若 \(p\) 是质数，且 \(a\) 与 \(p\) 互素，则 \(a^{p-1}\equiv 1 \pmod p\) 。

证明：

  • \(p-1\) 个整数 \(a,2a,3a,...,(p-1)a\)， 其中没有一个是 \(p\) 的倍数，且没有任意两个模 \(p\) 同余。

  • 所以这些数模 \(p\) 的余数是 \(1,2,3,…,(p-1)\) 的排列。

  • 于是得 \(a\times 2a \times 3a \times … \times (p-1)a \equiv 1 \times 2 \times ... \times (p-1) \pmod{p}\)

  • 可化简为 \(a^{p-1} \times (p-1)! \equiv (p-1)! \pmod p\)

  • 于是原命题得证。

那么据此我们就可以得到它的逆否命题：若 \(a^{m-1}\not\equiv 1 \pmod{m}\) , 则 \(m\) 不是质数。

但是这个命题不一定是正确的！事实上，对于伪素数（一种特殊的合数）中的卡迈克尔数，你就算把从 \(1\) 到那个数的所有质数都算一遍仍然是有问题的。那么就引出了我们的第二个引理——

前置知识-二次探测定理

对于一个奇质数 \(p\) (只有 \(2\) 不是奇质数)，则 \(x^2\equiv 1 \pmod p\) 的解为 \(x\equiv 1 \pmod{p}\) 或 \(x\equiv p-1 \pmod{p}\)。

证明：

  • 由 \(x^2\equiv 1 \pmod p\) 得 \(x^2-1\equiv 0 \pmod p\)
  • 即 \((x+1)(x-1)\equiv 0 \pmod p\)
  • 即 \(x+1 \equiv 0 \pmod p\) 或 \(x-1\equiv 0 \pmod p\)
  • 即 \(x \equiv p-1 \pmod p\) 或 \(x \equiv 1 \pmod p\)

知道了这些之后我们就可以愉快的进行判定了！

具体步骤

我们假定要判定的数 \(m\) 是一个奇素数，令 \(s=m-1\)，那么\(s\) 一定是偶数，可以分解成 \(s=2^k\times b\) 的形式。

我们首先根据费马小定理的“逆命题”，判断 \(m^{s}\equiv 1 \pmod m\) , 如果是那么我们就假定它是素数。

如果不是，根据二次探测定理，我们有

\[m^{s}\equiv s \pmod m\\ (m^{s})^2\equiv s \pmod m\\ {(m^{s})^2}^2\equiv s \pmod m\\ ...\\ {(m^{s})^2}^{b-1}\equiv s \pmod m \]

于是只要对系数不断平方直到：

  • 如果有一个式子成立，我们就暂且认为判定为素数，返回。
  • 如果每一个都不成立，我们就认为判定为合数，返回。

但是这不是一个确定性算法，也就是意味着这可能会判定失误。

所以我们需要选择多个和 \(m\) 互素的数进行判定，一般选 \(7\) 到 \(10\) 个，如果都给出素数结果，那么这个数一般就是素数。

时间复杂度 \(\mathcal O(k \log m)\)，\(k\) 为选择数的个数。

Code:

bool Miller_Rabin(int a,int n){
    int s=n-1,r=0;
    while(!(s&1)){s>>=1;r++;}
    long long k=qpow(a,s,n);
    if(k==1)return true;
    for(int i=0;i<r;i++,k=k*k%n/*可能溢出，用龟速乘*/){
		if(k==n-1)return true;        
    }
    return false;
}
bool isprime(int n){
    int times=8;
    int prime[100]={2,3,5,7,11,13,233,331};
    for(int i=0;i<times;i++){
        if(n==prime[i])return true;
        if(Miller_Rabin(prime[i],n)==false)return false;
    }
    return true;
}

例题

POJ-2089 Prime Distance

Link

题意：求区间 \([l,r]\) 范围内距离最大、最小的两个素数。（ $0\leq l < r \le 2.1\times 10^9 $ 且 \(r-l\leq 10^6\) ）

题解：可以用 #3 的方法筛出 \(\sqrt{2.1\times 10^9}\) 内的素数，也可以用 Miller_Rabin。

Code:

#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int n;
#define int long long
#define ll long long
int a[1000010],b[10000010],p[100010];
int cnt=0,l,r; 
void prime(int n){//线性筛
	cnt=0;
	b[1]=1;
	for(int i=2;i<=n;i++){
		if(!b[i]){
			p[++cnt]=i;
			for(int j=1;p[j]*i<=n;j++){b[p[j]*i]=1;if(i%p[j]==0)break;}
		}
	}
}
signed main(){	
	prime(50505);
	while(cin>>l>>r){
		int res=0,lst=0;int maxl=0,maxr=0,minl=-114514,minr=1919810;
		memset(a,0,sizeof a);
		for(int i=1;i<=cnt;i++){
			int pr=p[i];
			for(int j=max(pr*2,(l+pr-1)/pr*pr);j<=r;j+=pr)a[j-l]=1;
		}
		for(ll i=l;i<=r;i++){
			if(!a[i-l]&&i!=1){res++;
				if(res>=2){
					if(maxr-maxl<i-lst){maxr=i,maxl=lst;}
					if(minr-minl>i-lst){minr=i,minl=lst;}
				}
				lst=i;	
			}
		}
		if(res<2){cout<<"There are no adjacent primes."<<endl;}
		else{cout<<minl<<","<<minr<<" are closest, "<<maxl<<","<<maxr<<" are most distant."<<endl;}
	}
	return 0;
}

筛法

前置—质因数分解

把一个合数分解为几个素因数的乘积。

我们有唯一分解定理：若整数 \(n\ge 2\) ,那么 \(n\) 一定可以唯一的表示为若干素数的乘积，形如

\[n=p_1^{r_1}p_2^{r_2}...p_k^{r_k}(p_i\text{为素数},r_i>0) \]

时间复杂度 \(\mathcal O(\log n)\)。

Code:

vector<int> factor(int x){
    vector<int>ret;
    for(int i=2;i*i<=x;i++){
        while(x%i==0){ret.push_back(i);x/=i;}
        if(x==1)break;
    }
    if(x>1)ret.push_back(x);//素数
    return ret;
}

埃氏筛

全名：埃拉托斯特尼筛法。

首先我们知道质数的倍数一定是合数（这里的倍数不包括它本身）。

并且一个数的因子一定小于它（狭义的因子，定义见上）。

于是我们对于每一个素数都把它所有的倍数筛掉（一定是合数），那么遍历到它时没被筛掉的就一定是质数，拿它再做筛选。

如图:

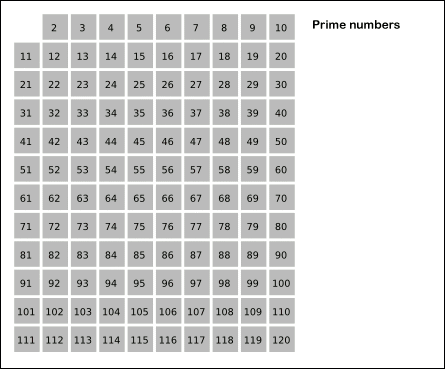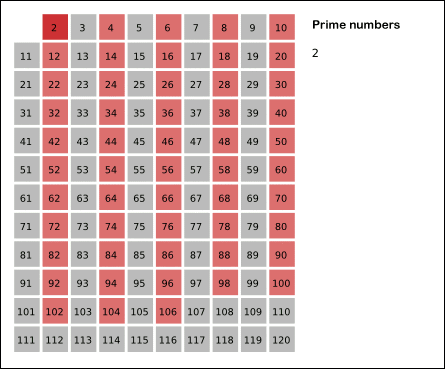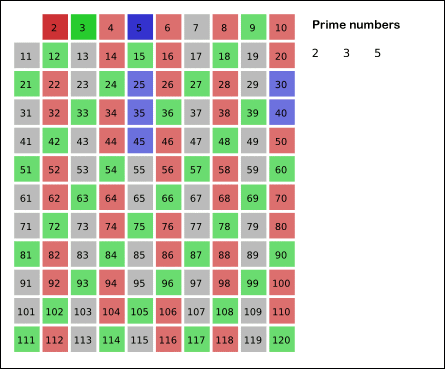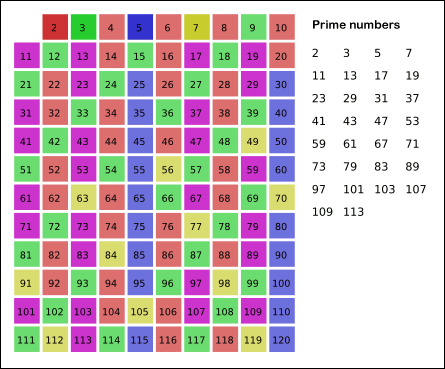
比较有意思的是它的复杂度。

我们首先看一个问题：

\(\mathcal O(\sum_{i=1}^n \frac{1}{i})\) 是多少？

答案：(link)

\[\begin{aligned} \mathcal O(\sum_{i=1}^n \frac{1}{i})&=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}...+\frac{1}{n}\\ &= \frac{1}{1}+(\frac{1}{2}+\frac{1}{3})+(\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7})+...+\frac{1}{n}\\ &\le 1+(\frac{1}{2}+\frac{1}{2})+(\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4})+...+\frac{1}{n}\\ &= 1+1+1+...+1\\ &= \log_2 n \end{aligned} \]

然而我们只需要对于每一个质数进行操作。 \([1,n]\) 范围内的质数约有 \(\log_2 n\) 个，加上遍历的复杂度，总复杂度为 \(\mathcal O(n \log \log n)\)。

Code:

bitset<1000010>b;
int prime[100010],cnt=0;
void prime(int n){
    for(int i=2;i<=n;i++)b[i]=0;
    for(int i=2;i<=n;i++){
        if(!b[i]){
            prime[++cnt]=i;
            for(int j=(long long)i*i;j<=n;j+=i)b[j]=1;
        }
    }
}
一些神秘的应用：质因数分解

我们可以在埃氏筛过程中记录每个合数的最小质因子，然后递归求解。

时间复杂度 \(\mathcal O(\log n)\)。

Code:

bitset<1000010>b;
int prime[100010],cnt=0;
int g[1000010];
void Eratos_prime(int n){
    for(int i=2;i<=n;i++)b[i]=0;
    for(int i=2;i<=n;i++){
        if(!b[i]){
            prime[++cnt]=i;g[i]=i;
            for(int j=(long long)i*i;j<=n;j+=i){
                if(!b[j]){b[j]=1;g[j]=i;}
            }
        }
    }
}
vector<int> factor(int x){
   Eratos_prime(x);vector<int>ret;
   while(x!=1){
       ret.push_back(g[x]);
       x/=g[x];
   }
   // if(x>1)ret.push_back(x);//素数
    return ret;
}

线性筛

又名：欧拉筛。

如果每个合数只被它的最小素因数筛除，那么每个数最多只筛一次。

具体步骤：

  • 枚举 \([2,n]\) 中的每一个整数 \(i\)：
  • 如果 \(i\) 是素数就保存在素数表中；
  • 利用 \(i\) 和素数表中的素数 \(p_j\) 去筛除 \(i\times p_j\) ，为了确保 \(i\times p_j\) 只被 \(p_j\) 筛过一次，要确保 \(p_j\) 是 \(i\times p_j\) 中最小的质因子，即 \(i\) 中不能有比 \(p_j\) 还小的素因子。

参考：(篇幅所限，只写了 \([2,10]\)筛 \([1,50]\) )

遍历的 \(i\) 筛除的 \(i\times p_j\)
\(2\) \(\{4\}\)
\(3\) \(\{6,9\}\)
\(4\) \(\{8,12\}\)
\(5\) \(\{10,15,25\}\)
\(6\) \(\{12,18\}\)
\(7\) \(\{14,21,35,49\}\)
\(8\) \(\{16\}\)
\(9\) \(\{18,27\}\)
\(10\) \(\{20\}\)

时间复杂度 \(\mathcal O(n)\)。

代码：

bitset<1000010>b;
int prime[100010],cnt=0;
void Prime(int n){
    for(int i=2;i<=n;i++){
        if(!b[i])prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
            b[i*prime[j]]=1;
            if(i%prime[j]==0)break;
        }
    }
}

标签：frac,数论,质数,int,素数,pmod,equiv
From： https://www.cnblogs.com/wang-yishan/p/17995206

相关文章

  • 【#C】练习题：请输出100以内的素数
    这里给出两种方法。素数就是指：除了能被1和自身整除，不能被其他数整除。这两种方法的思路，在根本上是一致的。例如对于34而言，在2~33内的如果能被34整除，就说明不是素数；如果在此范围内没有数能被34整除，就说明是素数。然后因为1不是素数，所以对2~100内的每个数进行判断。1、自定义函数法：运......
  • 数论总结
    一.定义\(\varphi(n)=\sum\limits_{i=1}^{n}[\gcd(i,n)=1]\)，即\(n\)以内与\(n\)互质的数的个数，叫做欧拉函数，念做/faɪ/。\(\mu(n)=\begin{cases}1&n=1\\0&\existsi\in[1,m],k_i>1\\(-1)^m&\foralli\in[1,m],k_i=1\end{cases}\)，记\(n=\pro......
  • 数论习题
    -P2568GCD给定\(n\)，求：\[\sum\limits_{p\in\mathbb{P}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[\gcd(i,j)=p]\]其中\(\mathbb{P}\)为质数集。推式子：\[\begin{aligned}\sum\limits_{p\in\mathbb{P}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[......
  • 数论习题
    -P2568GCD给定\(n\)，求：\[\sum\limits_{p\in\mathbb{P}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[\gcd(i,j)=p]\]其中\(\mathbb{P}\)为质数集。推式子：\[\begin{aligned}\sum\limits_{p\in\mathbb{P}}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[......
  • 基础数论大杂烩
    exgcd一，前置知识：裴蜀定理：若有\(a,b\)且\(a,b\)不全为0，则存在整数\(x,y\)，使得\(ax+by=gcd(a,b)\)。二，算法过程：作用：给定\(a,b,c\)，求解\(ax+by=c\)的整数解。我们先考虑求解\(ax+by=gcd(a,b)\)。由于\(gcd(a,b)=gcd(b,a\%b)\)，所以有：\(\begin{cases}ax_1+by_1=gcd(a,b)\\bx_......
  • 19素数
    19素数题目描述素数，也称质数，是指大于等于2且只能被1和它本身整除的正整数。输出100->200之间的素数的个数，以及所有的素数。输入格式无输出格式输出包含两行：第一行输出的素数的个数第二行输出100->200之间所有的素数，每个素数间用一个空格隔开，最后一个素数后无空格。样例输......
  • 数论题 推柿子
    自己重新推一遍柿子。/fendouP2568GCD题目传送门求\[\sum\limits_{p\inprime}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}[\gcd(i,j)=p]\]gcd的套路转换(\[\sum\limits_{p\inprime}\sum\limits_{i=1}^{\lfloor\frac{n}{p}\rfloor}\sum\limits_{j=1}^{\lfloor\f......
  • 数论分块
    数论分块算法简介能够在\(\mathcal{O(\sqrt{n})}\)的时间复杂度内计算出含有\(\sum\limits_{i=1}^{n}\left\lfloor\frac{k}{i}\right\rfloor\)等式子。令\(a_i=\left\lfloor\frac{k}{i}\right\rfloor\)，其主要思想为显然存在若干段连续区间内\(a_i\)值相同，......
  • 数论——Pollard-Rho 学习笔记
    数论——Pollard-Rho学习笔记非平凡因数：\(n\)除了\(1\)和\(n\)以外的因数。Pollard-Rho算法是一种用于快速分解非平凡因数的算法。Pollard-Rho能在期望复杂度\(\mathcalO(n^{1/4})\)的时间内找到\(n\)的最小的非平凡因数。而根据Pollard-Rho，我们可以用来加速质......
  • 数论——Fermat素性检验、Miller-Rabin素性检验
    数论——Fermat素性检验、Miller-Rabin素性检验试除法与素性测试试除法：所有的试除法，无论是\(\mathcalO(n)\)的还是\(\mathcalO(\sqrtn)\)的，其本质都相同：即找\(n\)可能存在的因子\(k\)，判断\(k\midn\)。素性测试：旨在不用分解因数的方式，判断一个数是否为质数；素性......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99