数论——Pollard-Rho 学习笔记

非平凡因数：\(n\) 除了 \(1\) 和 \(n\) 以外的因数。

Pollard-Rho 算法是一种用于快速分解非平凡因数的算法。

Pollard-Rho 能在期望复杂度 \(\mathcal O(n^{1/4})\) 的时间内找到 \(n\) 的最小的非平凡因数。

而根据 Pollard-Rho，我们可以用来加速质因数分解。

递归计算 \(n'=n/p\)，直到 \(n\) 为素数为止。

Pollard-Rho 的策略为：从 \([2,n)\) 中随机选取 \(k\) 个数 \(x_1,x_2,x_3,\dots,x_k\)，求任意两个数 \(x_i,x_j\) 的差和 \(n\)
的最大公约数，如果 \(1<d<n\)，则 \(d\) 为 \(n\) 的一个因子，直接返回 \(d\) 即可。

此时我们使用一个特殊的（并不随机的）随机函数来生成随机数：\(f(x)=(x^2+c)\bmod n\)。

这个函数生成的数是以一个环循环的，形如：

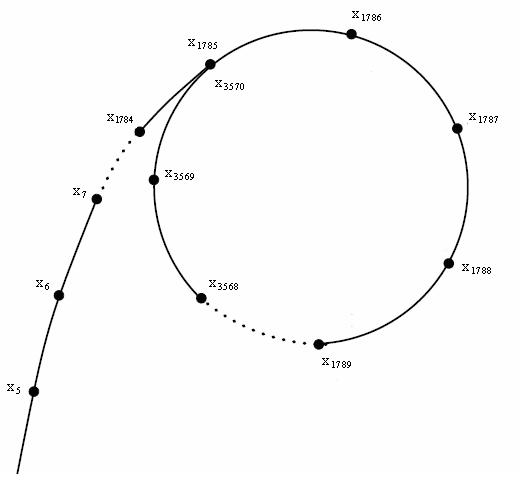
为什么用这个函数？根据生日悖论，生成的序列中不同值的数量约为 \(\mathcal O(\sqrt{n})\) 个。

设 \(m\) 为 \(n\) 的最小非平凡因子，显然有 \(m \le \sqrt n\)。

我们期望枚举 \(\mathcal O(\sqrt{m})\) 个 \(i\) 来分解出 \(n\) 的一个非平凡因子 \(\gcd(|x_i-x_j|,n)\)。

因此，Pollard-rho 算法能够在 \(\mathcal O(\sqrt{m})\) 的期望时间复杂度内分解出 \(n\) 的一个非平凡因子。

而 \(\mathcal O(\sqrt{m})\leq O(n^{1/4})\) ，那么 Pollard-rho 算法的期望时间复杂度为 \(\mathcal O(n^{1/4})\)。

代码：

mt19937 rd(time(0) * clock() + 19260817);
inline ll Abs(ll x) { return x < 0 ? -x : x; }
#define gcd(a, b) __gcd(a, b)

ll Pollard_Rho(ll x) {
    ll s = 0, t = 0, val = 1, d;
    ll c = (ll)rd() % (x - 1) + 1;
    for (int goal = 1; ; goal *= 2, s = t, val = 1) {
        for (ll step = 1; step <= goal; ++step) {
            t = ((__int128)t * t + c) % x;
            val = (__int128)val * Abs(s - t) % x;
            if (!val) return x;
            if (step % 127 == 0)
            if ((d = gcd(val, x)) > 1) return d;
        } if ((d = gcd(val, x)) > 1) return d;
    } return -1;
}

温馨提示：模板题 P4718 【模板】Pollard-Rho 并不是裸的模板。

但是也就是相当于再加上一道橙题难度的搜索就可以解决的。

Reference: https://oi-wiki.org/math/number-theory/pollard-rho/#pollard-rho-算法