一. 素数相关
0. 约定
若无特殊说明,本部分做以下记号规定。
\(p\in \mathbb{P}\),\(\mathbb P\) 为质数集。
\(\pi(n)\) 表示 \(1\) 至 \(n\) 内的素数个数。
\(P^{+}(n),P^-(n)\) 分别表示 \(n\) 的最大/最小质因子。
\(\nu_i\) 表示 \(i\) 的可重质因子个数。
1. 素数定理
\[\pi(x)\sim \frac x{\ln x} (x\rightarrow+\infty) \]\[\exists 0<a<b,\quad s.t.\frac {ax}{\ln x}<\pi (x)<\frac {bx}{\ln x} \]常用于估算素数数组大小。
2. 筛法
埃氏筛不展开。
欧拉筛保证合数只被筛一次,复杂度 \(O(n)\)。即线性筛。
同时通过欧拉筛容易实现对于欧拉函数,莫比乌斯函数的预处理。
3. 判断素数
- 暴力。
暴力的 \(O(\sqrt n)\) 是一种准确素性测试算法的复杂度。
- \(\text{Miller-Rabin}\) 算法
Miller-Rabin 使用费马小定理和二次探测定理进行素性测试。
显然根据费小和二次探测有
\[a^{p-1}\equiv 1\pmod p \]\[\forall x^2\equiv 1\pmod p, x\equiv\pm 1\pmod p \]设需要检验素性的数为 \(x\)。取 \(y<x\),那若 \(x\) 为质数则 \(y^{x-1}\equiv 1\pmod x\)。
再令 \(x-1=t\times 2^k\)。
根据二次探测定理,考虑对 \(y^{t\times 2^k}\) 不断开方,有
\[\exists 0\leq k'<k,y^{t\times 2^{k'}}\equiv-1\pmod x \]或 \(y^t\equiv 1\pmod x\)。
我们如此地对于 \(x\) 进行 \(m\) 次测试,复杂度是 \(O(m\log^3x)\)。但当然这是个概率算法。
一组常用的底数是 \(\{2,3,7,61,24251\}\)。在 \(10^{16}\) 内仅 \(46856248255981\) 发生误判。
#define int long long
int base[15]={0,2,3,7,61,24251};
inline bool Miller_Rabin(int n){
if(n<2||n==46856248255981ll)return false;
int t=n-1,k=0;
while(t%2==0){
t>>=1;
k++;
}
for(int i=1;i<=5&&base[i]<n;i++){
int x=qpow(base[i],t);
if(x==1)continue;
for(int j=1;j<k;j++)if(x!=n-1)x=(x*x)%n;
if(x!=n-1)return false;
}
return true;
}
4. \(\text{Meissel-Lehmer}\) 算法求 \(\pi (n)\)
以下令 \(p_i\) 表示第 \(i\) 个素数。\(p_1=2\)。
定义 \(\psi_i(n)=\sum\limits_{1\le x<n}[P^-(x)>p_i]\),\(\tau_i(n,k)=\sum\limits_{1\le x<n}\left([P^-(x)>p_i]\times [\nu_x=k]\right)\)。
由于容斥显然有
\[\psi_i(n)=\sum_{k\ge 0}\tau_i(n,k)[p_i^k\le n] \]其中钦定 \(\tau_i(n,0)=1\)。
考虑对于 \(n^{\frac{1}3}\le m\le n^{\frac{1}{2}}\),其中 \(m=p_{\omega}\)。
那么对于 \(k\ge 3\) 时有 \(\tau_{\omega}(n,1)=\pi(n)-\omega\),\(\tau_{\omega}(n,k)=0\)。
\[\therefore \pi(n)=\tau_{\omega}(n,1)+\omega=\psi_{\omega}(n)-\tau_{\omega}(n,2)-\tau_{\omega}(n,0)+\omega \]那么对于 \(\pi(n)\) 我们只需计算 \(\psi_{\omega}(n)\) 和 \(\tau_{\omega}(n,2)\) 即可。
- 计算 \(\tau_{\omega}(n,2)\)
考虑它的实际意义:即质数对 \((p,q)\) 满足 \(m<p\le q\) 且 \(pq\le n\) 的个数。
显然 \(p\in[m+1,\sqrt n]\),那么亦有 \(q\in[p,\frac{n}p]\),可得:
\[\tau_{\omega}(n,2)=\sum_{p\in [m+1,\sqrt n]}\left(\pi \left(\frac{n}p\right)-\pi (p-1)\right) \]此时线性筛预处理容易做到 \(O(\frac{n}{m})\)。
- 计算 \(\psi_{\omega}(n)\)
通过容斥有
\[\psi_{\omega}(n)=\psi_{\omega-1}(n)-\psi_{\omega -1}\left(\frac{n}{p_{\omega}}\right) \]边界 \(\psi_{0}(n)=[n]\)。
那么考虑 dfs 计算此式,此时复杂度难以接受。考虑对于边界加入 \(x\le m\) 的剪枝。
\[\psi_{\omega}(n)=\sum_{x\le m}\mu(x)\left[\frac{n}{x}\right]+\sum_{\frac{x}{P^{-}(x)}\le m<x}\mu(x)\psi_{\pi\left(P^{-}(x)\right)-1}\left(\frac{n}{x}\right) \]令
\[R=\sum_{x\le m}\mu(x)\left[\frac{n}{x}\right] \]\[T=\sum_{\frac{x}{P^{-}(x)}\le m<x}\mu(x)\psi_{\pi\left(P^{-}(x)\right)-1}\left(\frac{n}{x}\right) \]\[\therefore \psi_{\omega}(n)=R+T \]显然 \(R\) 容易预处理。
对于
\[T=-\sum_{p\le m}\sum_{x\le m<xp}\left[P^-(x)>p\right]\mu(x)\psi_{\pi (p)-1}\left(\frac{n}{xp}\right) \]考虑分块计算,令
\[T_1=-\sum_{n^{\frac{1}3}<p\le m}\sum_{x\le m<xp}\left[P^-(x)>p\right]\mu(x)\psi_{\pi (p)-1}\left(\frac{n}{xp}\right) \]\[T_2=-\sum_{n^{\frac{1}4}<p\le n^{\frac{1}3}}\sum_{x\le m<xp}\left[P^-(x)>p\right]\mu(x)\psi_{\pi (p)-1}\left(\frac{n}{xp}\right) \]\[T_3=-\sum_{p\le n^{\frac{1}4}}\sum_{x\le m<xp}\left[P^-(x)>p\right]\mu(x)\psi_{\pi (p)-1}\left(\frac{n}{xp}\right) \]\[\therefore T=T_1+T_2+T_3 \]首先 \(T_3\) 显然通过树状数组枚举 \(p\) 统计对 \(\psi\) 的贡献在 \(O(\frac{n}m\log n)\)
简单实现。
对于 \(T_1,T_2\) 由于 \(n^{\frac{1}4}<p<P^-(x),x\le m\le \sqrt n\),故必有 \(x\in \mathbb P\)。
\[\therefore T_1=-\sum_{n^{\frac{1}3}<p\le m}\sum_{p<q\le m}\psi_{\pi (p)-1}\left(\frac{n}{pq}\right) \]\[\therefore T_2=-\sum_{n^{\frac{1}4}<p\le n^{\frac{1}3}}\sum_{p<q\le m}\psi_{\pi (p)-1}\left(\frac{n}{pq}\right) \]考虑计算 \(T_1,T_2\)。
\(T_1\) 由于 \(\frac{n}{pq}<n^{\frac{1}3}<p\) 故 \(\psi_{\pi (p)-1}\left(\frac{n}{pq}\right)=1\),所以 \(T_1\) 容易 \(O(m)\) 计算:
\[T_1=-\sum_{n^{\frac{1}3}<p\le m}\left(\pi(m)-\pi(p)\right) \]对于 \(T_2\) 再次拆开为 \(S_1+S_2=T_2\):
\[S_1=\sum_{n^{\frac{1}{4}}<p\le n^{\frac{1}3}}\sum_{p<q\le m}\left[q\le \frac{n}{p^2}\right]\psi_{\pi(p)-1}\left(\frac{n}{pq}\right) \]\[S_2=\sum_{n^{\frac{1}{4}}<p\le n^{\frac{1}3}}\sum_{p<q\le m}\left[q>\frac{n}{p^2}\right]\psi_{\pi(p)-1}\left(\frac{n}{pq}\right) \]对于 \(S_1\) 由于有 \(p\le \frac{n}{pq}< \sqrt n< p^2\),故有 \(\psi_{\pi(p)-1}\left(\frac{n}{pq}\right)=\pi\left(\frac{n}{pq}\right)-\pi(p)+1\)
。
然后你再分为 \(S_1=Q_1+Q_2\),
\[Q_1=\sum_{n^\frac{1}{4}< p\leq n^\frac{1}{3}}(1-\pi(p))\sum_{{p< q\le m}}\left[q\leq \frac{n}{p^2}\right] \]\[Q_2=\sum_{n^\frac{1}{4}< p\leq n^\frac{1}{3}}\sum_{{p<q\leq m }}\left[q\leq \frac{n}{p^2}\right]\pi\left(\frac{n}{pq}\right) \]我们发现 \(Q_1\) 简单处理即可,对于 \(Q_2\) 进行类数论分块只有 \(\pi(\frac{n}{p^2})\) 块,所以保证 \(O\left(\frac{n^{\frac{2}3}}{\log n}\right)\)。
对于 \(S_2\),有 \(\sqrt{\frac{n}m}\le\sqrt{\frac{n}q}<p\) 且 \(\frac{n}{pq}<p\) 故 \(\psi_{\pi(p)-1}\left(\frac{n}{pq}\right)=1\)。
\[\therefore S_2=\sum_{\sqrt{\frac{n}{m}}<p\le n^{\frac{1}3}}\left(\pi(m)-\pi\left(\min\left\{p,\frac{n}{p^2}\right\}\right)\right) \]复杂度 \(O(m)\)。
考虑整个过程的时间复杂度计算。令 \(m=O(n^{\frac{1}3}\log^2n)\) 时复杂度最优为 \(O\left(\frac{n^{\frac{2}{3}}}{\log n}\right)\)。
若将 \(Q_2\) 分为五个部分计算(参见oi-wiki),可优化至 \(O\left(\frac{n^{\frac{2}{3}}}{\log^2 n}\right)\)。
常数极大的代码。比最优解慢了近40s。
inline void init(){
Getprime();
sz[0]=1;
for(int i=0;i<S;i++)phi[i][0]=i;
for(int i=1;i<=2;i++){
sz[i]=p[i]*sz[i-1];
for(int j=1;j<S;j++)phi[j][i]=phi[j][i-1]-phi[j/p[i]][i-1];
}
return;
}
inline int Phi(int x,int id){
int P=p[id],r=sz[id];
if(!id)return x;
if(id<=2)return phi[x%r][id]+(x/r)*phi[r][id];
if(x<=P*P)return pi[x]-id+1;
if(x<=P*P*P&&x<N){
int y=sqrt2(x),t=pi[y],res=pi[x]-((t-id+1)*(t+id-2)>>1);
for(int i=id+1;i<=t;i++)res+=pi[x/p[i]];
return res;
}
return Phi(x,id-1)-Phi(x/p[id],id-1);
}
inline int Pi(int x){
if(x<N)return pi[x];
int X=Pi(sqrt2(x)),Y=Pi(sqrt2(sqrt2(x))),Z=Pi(sqrt3(x)),res=Phi(x,Y)+((X+Y-2)*(X-Y+1)>>1);
for(int i=Y+1;i<=X;i++){
int t=x/p[i];res-=Pi(t);
if(i>Z)continue;
int O=Pi(sqrt2(t));
for(int j=i;j<=O;j++)res-=Pi(t/p[j])-j+1;
}
return res;
}
-
参考文献:
5. \(\text{Pollard-Rho}\) 算法计算非平凡因子
对于寻找合数 \(n\) 的一种非平凡因子的朴素做法显然可以枚举 \([1,\sqrt n]\) 来做到。当然你还可以通过预处理一点打表来达到 \(O(\frac{\sqrt n}{\ln n})\)。
生日悖论是一个著名的问题。
钦定有 \(n\) 个人,一年 \(m=365\) 天。
那么 \(n\) 个人中没有任意两人生日相同的概率为
\[P=\prod_{i=1}^{n}\frac{m-i+1}{m} \]那么反之存在二人生日相同即为 \(1-P\)。
\[\because 1+x\le e^x \]\[\therefore P\le \prod_{i=1}^{n}e^{-\frac{i-1}{m}}=e^{-\frac{n(n-1)}{2m}} \]而著名的悖论在于带入 \(n=23\) 即有 \(P\le 50\%\)。由于反直觉被认为是悖论。
事实上在 \(n=\sqrt{\frac{m}{\ln 2}}\) 左右时有 \(P=50\%\)。
考虑一个随机序列 \(X\) 由 \(f(x)=x^2+c\pmod n\) 生成。\(c\) 随机。
那么这个序列 \(X\) 在出现 \(x_i=x_j,i<j\) 时,\(X\) 就从 \(i\) 开始陷入循环。
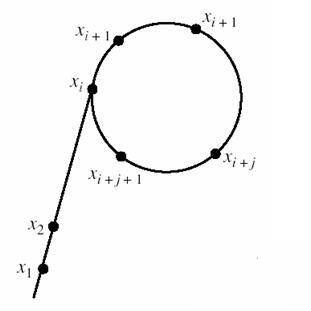
即如上图所示,因其形像 \(\rho\) 而成为 \(\text{rho}\)。
那么这样的“伪随机”序列 \(X\) 产生环的期望其上述的生日悖论。
设 \(m\) 为 \(n\) 的最小非平凡因子。显然 \(m\le \sqrt n\),再记 \(y_i=x_i\pmod m\)。
\[\begin{aligned}\therefore y_{i+1}&=x_{i+1}\pmod m \\ & = x_i^2+c\pmod m\\&=(x_i\bmod m)^2+c\pmod m\\&=y_i^2+c\pmod m\end{aligned} \]那么对于新的序列 \(Y\),若存在 \(i,j\) 使 \(x_i\neq x_j\) 且 \(y_i=y_j\),即 \(m\mid |x_i-x_j|,n\nmid |x_i-x_j|\).
那么令 \(g=\gcd(|x_i-x_j|,n)\),\(g\) 必然是 \(n\) 的一个非平凡因子。
期望枚举 \(O(\sqrt m)\) 次来获得 \(g\)。而 \(m\le \sqrt n\),故期望 \(O(n^{\frac{1}{4}})\)。
考虑优化。
- \(\text{Floyd}\) 判环
即通过双指针 \(i,j\),其中 \(i\) 的速度是 \(j\) 的两倍,以此去遍历环,那么 \(i,j\) 相遇时是环长整数倍。当然还是检查 \(g=\gcd(|x_i-x_j|,n)\)。复杂度 \(O(\sqrt[4] n\log n)\)。这里不做赘述。
- 倍增优化
多次求 \(\gcd\) 是时间复杂度的瓶颈,考虑如何优化。
每次将 \(|x_i-x_j|\) 相乘,若对于一对 \(x_I,x_J\),有 \(g\) 为 \(m\) 的非平凡因子,那么设 \(S=\prod|x_i-x_j|\),必然有 \(g'=\gcd(S,n)\) 亦为 \(n\) 的非平凡因子。
那么考虑累计到一定样本再进行 \(\gcd\)。考虑将阈值设为倍增,每次判断 \(g'<n\) 即可。
6. 反素数
素数是因子只有两个的数,反素数就是因子最多的数而不是emirp,并且因子个数相同的时候值最小。显然反素数是相对于一个集合的。
考虑对于一个反素数 \(n=\prod\limits_{i=1}^m p_i^{k_i}\),即有 \(\prod\limits_{i=1}^m(k_i+1)\) 取 \(\max\)。
考虑在给定范围内如何求反素数。
显然直接分解质因数无法接受。考虑反素数的性质。
- 反素数是从 \(2\) 开始的连续素数的幂次形式乘积。
显然。所以考虑 \(\min m\) 使 \(\prod\limits_{i=1}^{m+1}>n\),我们只需枚举前 \(m\) 个素数。
- 数值小的素数的幂次大于等于数值大的素数,即 \(k_1\ge k_2\ge \cdots \ge k_m\)。
还是显然。若有 \(k_i<k_j,i<j\) 则将 \(k_j-k_i\) 移至 \(p_i\) 幂次上更优。那么最坏枚举幂次枚举至 INT_MAX 差不多 \(64\) 即可。
整个过程就容易用搜索实现。
\(\text{CF27E}\)。模板题。
inline void dfs(int x,int k,int m,int dep){
if(dep>n||x<=0ll||x>=ans||k>16)return;
if(dep==n){
ans=x;
return;
}
x*=p[k];
for(int i=1;i<=m;i++,x*=p[k])dfs(x,k+1,i,dep*(i+1));
return;
}
二. \(\text {gcd}\) 相关
1. 求 \(\gcd\)
显然通过欧几里得/辗转相除容易在 \(O(\log n)\) 时间内递归求出 \(\gcd\)。
inline int gcd(int x,int y){
if(!y)return x;
return gcd(y,x%y);
}
考虑一个问题:求一组可行解 \((x,y)\) 满足 \(ax+by=\gcd(a,b)\)
设 \(ax_1+by_1=\gcd(a,b)\),\(bx_2+(a\bmod b)y_2=\gcd(b,a\bmod b)=\gcd(a,b)\)。
\[\therefore ax_1+by_1=bx_2+(a\bmod b)y_2=bx_2+(a-b\left\lfloor \frac{a}{b}\right\rfloor )y_2 \]故 \(x_1=y_2,y_1=x_2-\left\lfloor \frac{a}{b}\right\rfloor y_2\)
那么剩余的按照普通的欧几里得递归做就行。
inline int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1,y=0;
return a;
}
int res=exgcd(b,a%b,x,y),X=x;
x=y,y=X-(a/b)*y;
return res;
}
2. 裴蜀定理
\(\forall a,b\in \mathbb Z(a\ or\ b\neq 0),\exists x,y\in\mathbb Z,ax+by=\gcd(a,b)\)。
证明:
设 \(g=\gcd(a,b),s=\min(ax+by)\in \mathbb N_+,t=\left\lfloor\frac{a}{s}\right\rfloor\),显然 \(\forall x,y\in \mathbb Z\) 有 \(g|ax+by\)。
\[\therefore a\bmod s=a-t(ax+by)=a(1-xt)+b(-yt) \]那么 \(a\bmod s\) 是 \(a,b\) 的线性组合。同时有 \(0\le a\bmod s<s\)。再由 \(s\) 定义易知 \(a\bmod s=0\)。同理亦有 \(s|b\)。故 \(s\) 为 \(a,b\) 公约数。故 \(g\ge s\)。
又因为 \(g|a,g|b\) 且 \(s\) 为 \(a,b\) 线性组合。显然 \(g|s\)。那么即得 \(g=s\)。
裴蜀定理的一个推论:\(a,b\) 互质的充要条件是存在 \(x,y\in \mathbb Z\) 使 \(ax+by=1\)。此不做赘述。
那么这可看做是上述 exgcd 的一个补充。
3. 类欧几里得
虽然我并不知道这放在这个专题是否合适