数论分块

数论分块

算法简介

能够在 \(\mathcal{O(\sqrt{n})}\) 的时间复杂度内计算出含有 \(\sum\limits_{i = 1}^{n} \left \lfloor \frac{k}{i} \right \rfloor\) 等式子。

令 \(a_i = \left \lfloor \frac{k}{i} \right \rfloor\)，其主要思想为显然存在若干段连续区间内 \(a_i\) 值相同，那么我们就可以将一个块内的 \(a_i\) 一起计算，可以做到 \(\mathcal{O(\sqrt{n})}\) 的时间复杂度。

举例说明：

当 \(k = 10\) 时，我们可以作出以下表格：

当然，也可以作出以下 \(y = \frac{10}{x}\) 的反比例函数图像。

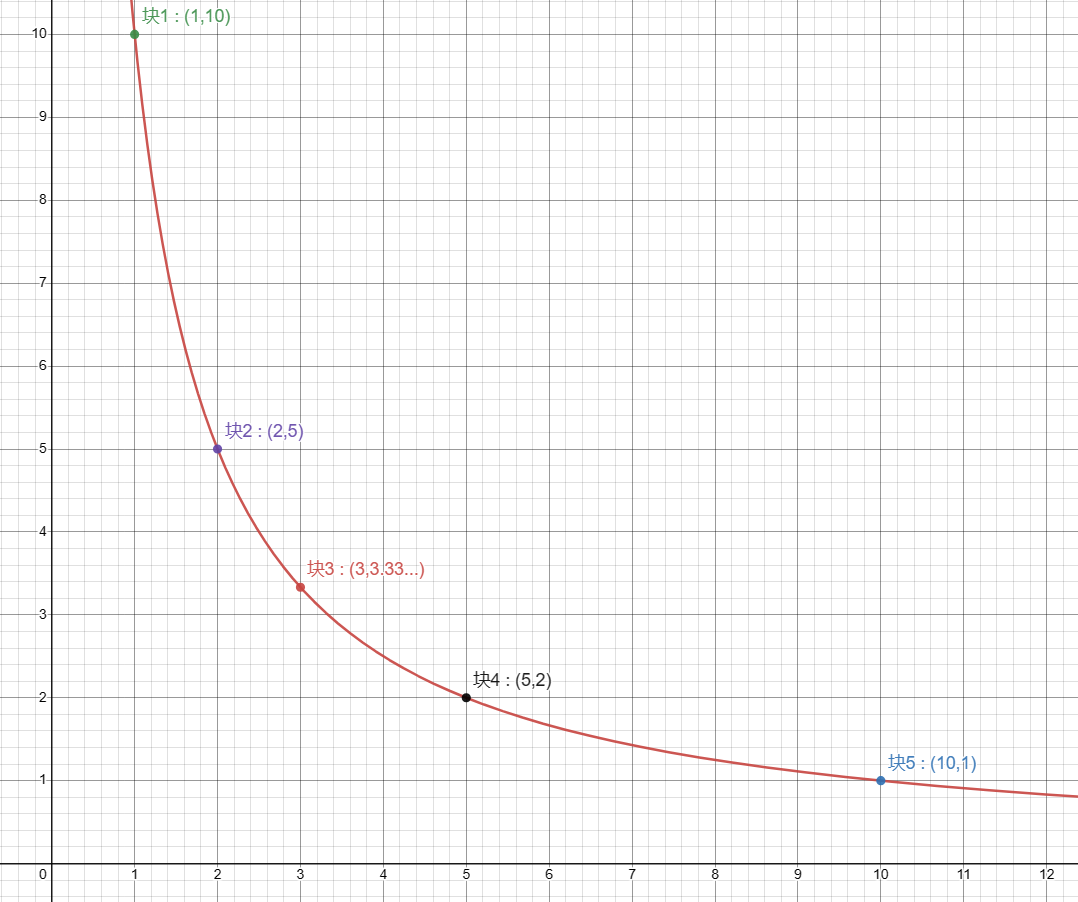
可以看到，\(4 \sim 5\) 以及 \(6 \sim 10\) 这两个连续段内 \(a_i\) 的值均相同。

算法过程

我们考虑如何去求每个块内的值。

可以发现对于每个块，我们可以通过递推计算得到其块内的值 \(val\)，以及整个块的左右端点 \(l,r\)。

显然，其中 \(val = \left \lfloor \frac{k}{i} \right \rfloor,r = \left \lfloor \frac{k}{\left \lfloor \frac{k}{i} \right \rfloor} \right \rfloor\)，\(l\) 的值可以根据上一次的 \(r' + 1\) 得来。

对于 \(r = \left \lfloor \frac{k}{\left \lfloor \frac{k}{i} \right \rfloor} \right \rfloor\)，有证明：

显然 \(val = \left \lfloor \frac{k}{i} \right \rfloor\)，\(val \leq \frac{k}{i}\)，那么 \(i = \left \lfloor \frac{i}{\frac{k}{i}} \right \rfloor\)，\(i \leq \left \lfloor \frac{k}{val} \right \rfloor\)，所以 \(i\) 最大值即为 \(\left \lfloor \frac{k}{val} \right \rfloor = \left \lfloor \frac{k}{\left \lfloor \frac{k}{i} \right \rfloor} \right \rfloor\)。

P2261 [CQOI2007] 余数求和

对于这道题，我们就能写出如下代码：

int res = k * n;
for (int l = 1,r; l <= n; l = r + 1 ) {
	if (k / l) r = min(n,k / (k / l));
	else r = n;
	res -= (l + r) * (r - l + 1) / 2 * (k / l);
}
printf("%lld\n",res);