tarjan学习笔记

0.前置知识

• 强连通图

  在一个有向图中，若从任意一点可以到达其他所有点，则称之为强连通图

• 强连通分量（SCC）

  一个图中的极大强连通性质子图（强连通图的强连通分量是它本身）

  \(\small {极大强连通子图指一个不能加入另外的点的强连通子图（一个强连通子图可能包含一个或多个小的强连通子图）}\)

• dfn（时间戳）

  在对图的遍历中，各个顶点被遍历的顺序（ \(dfn[i]\) 表示节点 \(i\) 第几次被遍历到）

• low（追溯值）

  可以理解为，在一个节点存在的路径中，最小的 \(dfn\) 值（ \(low[i]\) 表示在节点 \(i\) 存在的路径中，最小的 \(dfn\) 值）

• 搜索树

  在一张连通图中，所有的节点以及发生递归的边共同构成一棵搜索树。如果这张图不连通，则构成搜索森林。
  

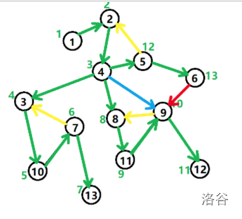
  如图 从lrb博客上扣下来的

  • 搜索树上的边，称为 树边（绿色）。
  • 从祖先指向后代的非树边，称为 前向边（蓝色）。
  • 从后代指向祖先的非树边，称为 返祖边（黄色）。
  • 从子树中的节点指向另一子树节点的边，称为 横叉边（红色）。

1. tarjan求有向图强连通分量

• 强连通分量判定法则

  其实是求一个节点属于哪个强连通分量

  • \(low\) 的更新方式

    设 当前访问的节点为 \(x\), \(x\) 能到达的点为 \(y\)

    • 初始化 dfn[x]=low[x]=++tot

    • 若 \(y\) 未被遍历到，则该边为树边，递归访问 \(y\) , 因为 \(low\) 的性质，令low[x]=min(low[x],low[y])

    • 若 \(y\) 被遍历过且在栈中，则该边为返祖边或横叉边（存疑），因为 \(low\) 的性质,可以回到 \(x\)，令low[x]=min(low[x],low[y])

  • 主要判断方式

    dfn[x]==low[x] 可以理解为 节点 \(x\) 能返回到最早的节点就是 \(x\) 本身,则节点 \(x\) 到 \(s.top()\) 内的所有节点为一个强连通分量。

  • 常用变量

    cnt：强连通图数量

    dfn[]：节点 \(i\) 第几次被遍历到

    low[]：在节点 \(i\) 存在的路径中，最小的 \(dfn\) 值

    belong[]：节点 \(i\) 属于第几个强连通图

    inStack[]：节点 \(i\) 是否在栈中

    tot：当前已有几个节点被访问

  • 代码实现

  inline void tarjan(int x){
      dfn[x]=low[x]=++tot;
      s.push(x);
      inStack[x]=1;
      for(int i = Head[x];i;i=Next[i]){
          int y=Ver[i];
          if(!dfn[y]){
              dfs(y);
              low[x]=min(low[x],low[y]);
          }
          else 
              if(inStack[y])low[x]=min(low[x],low[y]);
      }
      if(dfn[x]==low[x]){
          cnt++;
          while(s.top()!=x){
              belong[s.top()]=cnt;
              inStack[s.top()]=0;
              s.pop();
          }
          inStack[x]=0;
          belong[x]=cnt;
          s.pop();
          
      }
  }
  

• 缩点

  因为一个节点只属于一个强连通分量，所以对于一些问题，我们可以将一个强连通分量看做一个点。

  即若存在有向边 x->y，若 belong[x]!=belong[y] 则建立一条边 belong[x] -> belong[y]。

  • 代码实现

  for(int i = 1;i <= n;i++){
      for(int j=A.Head[i];j;j=A.Next[j]){
          int y=A.Ver[j];
          if(belong[i]!=belong[y]){
              A_.add(belong[i],belong[y]);
              outp[belong[i]]++;
          }
      }
  }
  

  \(\small{ps：A,A\_ 为封装的链式前向星。}\)