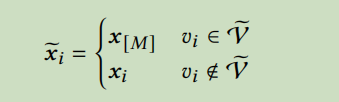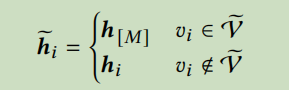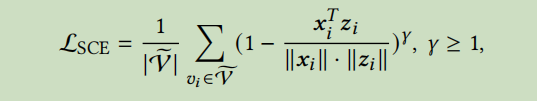GraphMAE阅读
引言
在摘要里,本论文提出了自监督学习有着巨大的潜力
自监督学习又分为对比学习和生成学习
目前比较成功的是对比学习,因为在对比学习中,有高质量的数据增强以及可以通过额外的策略来稳定训练过程
而对于生成式的自监督学习,它们旨在重建数据本身的特征和信息,对图来说,图自动编码器(Graph Autoencoder, GAE)可以重建图的结构信息或者节点特征,但是目前基于图自动编码器的发展远远落后于对比学习
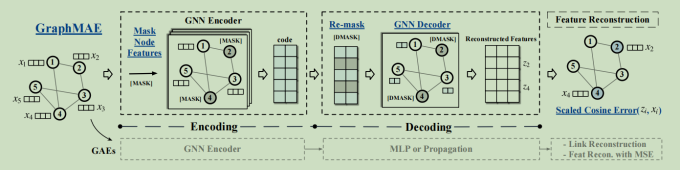
所以,本文提出了GraphMAE,GraphMAE发现仅仅重建节点特征便能够使得模型学到充分的信息,从而有助于下游分类等任务。
GraphMAE的主要改进包括:
- 带掩码的节点特征重建
- 使用放缩余弦误差
- 带重掩码的解码过程
GraphMAE的结构
1.带有MASK的节点特征重建
对于一个图\(G=(V,\varepsilon,X)\)
从图中采样部分节点\(\tilde{V}\subset V\),用一个掩码标识[MASK]来替换它们的输入节点特征,记经过mask之后的节点特征矩阵为\(\tilde{X}\),那么
2.带重掩码的解码过程
传统的decoder的表现力较差,导致encoder得到的节点表示H与输入特征几乎相同,所以GraphMAE采用了单层图神经网络作为decoder,GNN decoder可以根据一个节点周围的节点分布恢复其自身的输入特征,可以帮助解码器学习高层次的信息
GraphMAE采用一种新的重掩码的方式,用另一个掩码标识[DMASK],再次替换最初采样到的节点的表示。即
这样就可以迫使从邻近的未遮盖的节点中重构它的输入特征
3.使用放缩余弦误差
之前的图自动编码器大多数采用均方误差作为损失函数,但是均方误差在训练中最小化到接近零或者很难优化,不足以进行有意义的特征重建。所以GraphMAE采用了余弦误差,同时引入了放缩因子来进一步改进余弦误差。当放缩因子大于1时误差能够更快的衰减到0,从而能够调整难度不同样本的权重,放缩余弦误差的定义为:
放缩因子也是一个在不同数据集上可调整的超参数
标签:误差,GraphMAE,特征,笔记,放缩,阅读,掩码,节点 From: https://www.cnblogs.com/anewpro-techshare/p/17728234.html