前言

OI 中，多项式有着十分广泛的应用。其基础是多项式的基本运算，几乎所有多项式运算都是由多项式加法和乘法拼接成的。我们有显然的 \(O(n)\) 的办法计算多项式加法，而朴素的多项式乘法是很多情况下难以接受的 \(O(n^2)\) 的复杂度。快速傅里叶变换（FFT）可以高效（\(O(n\log n)\)）计算多项式乘法，因此成为了多项式科技中几乎最重要的基础。

这篇总结是对 FFT 核心原理的一个不严谨的描述。

FFT

Part 1. 多项式的表示

对于一个多项式，\(f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n\)，我们称它的次数为 \(n\)，项数为 \(n+1\)，任意大于等于 \(n\) 的正整数都叫 \(f(x)\) 的次数界。

由多项式的定义，我们可以用长度为 \(n+1\) 的向量 \(\begin{bmatrix}a_0,a_1,a_2,\dots,a_n \end{bmatrix}\) 来表示这个多项式。我们称这种表示方式为多项式的系数表示。

考虑把多项式 \(f(x)\) 视作平面直角坐标系上的函数，如果我们知道 \(n+1\) 个横坐标不同的点 \((x_0,y_0),(x_1,y_1)\dots,(x_n,y_n)\) 在其图象上，可以列出线性方程组：

\(\begin{cases}a_0+x_0a_1+x_0^2a_2+\dots+x_0^na_n=y_0\\a_0+x_1a_1+x_1^2a_2+\dots+x_1^na_n=y_1\\ \qquad \dots \qquad \dots \\ a_0+x_na_1+x_n^2a_2+\dots+x_n^na_n=y_n \end{cases}\)

由线性代数知识（链接） 可知，该方程组有唯一解 \((a_0,a_1,a_2,\dots,a_n )\)。

这表明，我们可以通过 \(n+1\) 个横坐标互不相同的点表示一个 \(n\) 次多项式。事实上，给定这 \(n+1\) 个点的横纵坐标，我们可以通过高斯消元（\(O(n^3)\)）或拉格朗日插值（\(O(n^2)\)）计算出多项式的系数。

点值表示的多项式有个好处是：如果我们知道两个 \(n\) 次多项式 \(A,B\) 的点值表示，取了 \(2n+1\) 个点，并且取的 \(2n+1\) 个点的横坐标对应相同，我们可以 \(O(n)\) 的计算出多项式 \(A\times B\) 在这 \(2n+1\) 个点的值，进而可以算出 \(A\times B\) 的系数表示。

这样我们找到了一种新的计算多项式乘法的方式，先想办法求出 \(A,B\) 各自在某 \(2n+1\) 个点的取值，再 \(O(n)\) 计算每个位置点值乘积，再想办法把这些点值变成系数表示。也就是下面这张经典的关系图：

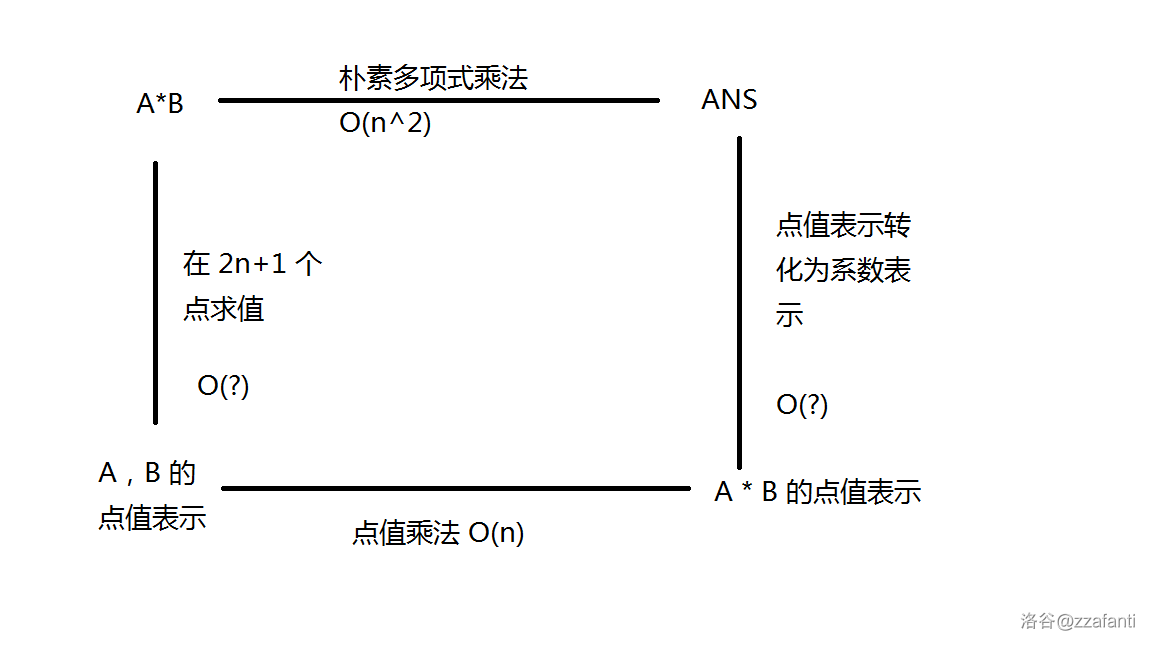
Part 2. 离散傅里叶变换（DFT）

假设我们要计算 \(m_1\) 次多项式 \(A\) 和 \(m_2\) 次多项式 \(B\) 的乘积，设 \(n\) 是大于 \(m_1+m_2\) 的最小的 2 的整次幂。

我们希望在 \(O(n\log n)\) 的时间内计算 \(n\) 个点在 \(A\) 的取值。随意选点至少要 \(O(n^2)\) 的时间计算点值。所以我们要在选的点上做文章。

我们引入复数单位根。设 \(n\) 是 2 的整次幂，则 \(w_n=\cos(\frac{2\pi}{n})+i\sin(\frac{2\pi}{n})\)。其几何意义是复平面上直线 \((0,0)\) - \((1,0)\)，逆时针旋转 \(\frac{2\pi}{n}\) 弧度，与单位圆的交点。

记 \(w_n^u=\cos(\frac{2\pi u}{n})+i\sin(\frac{2\pi u}{n})\)

不难验证复数单位根有以下性质：

• \(w_n^0=1\)

• \(w_n^a \times w_n^b = w_n^{a+b}\) （可通过三角恒等式验证）

• \(w_n^a=w_n^{a\bmod n}\)

• \(w_{dn}^{dk}=w_n^k\)，也称作消去引理

• \(w_{n}^{d}=-w_{n}^{d+\frac{n}{2}}\)

我们要去求出 \(A(w_n^0),A(w_n^1),\dots,A(w_n^{n-1})\)。

设多项式 \(A_0=a_0+a_2x+a_4x^2+\dots+a_{n-2}x^{\frac{n-2}{2}}\)，\(A_1=a_1+a_3x+a_5x^2+\dots+a_{n-1}x^{\frac{n-2}{2}}\)。那么

\(\begin{aligned} &A=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1} \\ &=A_0(x^2)+xA_1(x^2)\end{aligned}\)

根据消去引理，\((w_n^k)^2=w_{\frac{n}{2}}^k\)。又因为 \(w_{\frac{n}{2}}^k=w_{\frac{n}{2}}^{k\bmod \frac{n}{2}}\) 所以实际用到的 \(A_0\) 和 \(A_1\) 的点值各自只有 \(\dfrac{n}{2}\) 个。递归计算 \(A_0\) 和 \(A_1\) 在这些点处的取值，可以做到 \(O(n)\) 合并出 \(A\) 的点值。

时间复杂度 \(T(n)=2T(\dfrac{n}{2})+O(n)=O(n\log n)\)

至此，我们完成了在 \(n\) 次复单位单位根处多项式 \(A\) 的点值的计算。

Part 3. 逆离散傅里叶变换（IDFT）

我们求出了 \(A\) 和 \(B\) 在 \(n\) 个复单位根处的取值，将对应点点值相乘，得到答案多项式 \(C\) 在这些点的取值， \(\{(w_n^0,C(w_n^0)),(w_n^1,C(w_n^{1})),\dots,(w_n^{n-1},C(w_n^{n-1}))\}\)。

设多项式 \(F(x)=C(w_n^0)+C(w_n^1)x+C(w_n^2)x^2+\dots+C(w_n^{n-1})x^{n-1}\)。设 \(C\) 的 \(i\) 次项的系数为 \(c_i\)，将 \(w_n^{-k}\) 带入 \(F(x)\) 得：

\(\begin{aligned} & F(w_n^{-k})\\ &=\sum\limits_{i=0}^{n-1}C(w_n^i)w_n^{-ik} \\& =\sum\limits_{i=0}^{n-1} w_n^{-ik} \sum\limits_{j=0}^{n-1} c_j w_n^{ij} \\ & =\sum\limits_{j=0}^{n-1} c_j \sum\limits_{i=0}^{n-1} w_n^{i(j-k)} \end{aligned}\)

设 \(T=\sum\limits_{i=0}^{n-1} w_n^{i(j-k)}\)。

我们有 \(w_n^{j-k}T=\sum\limits_{i=1}^{n} w_n^{i(j-k)}\)

进而，\((w_n^{j-k}-1)T=w_n^{n(j-k)}-w_n^{0}=0\)

如果 \(j=k\) 那么显然 \(T=n\)

否则 \(w_n^{j-k}-1\neq 0\)，\(T=0\)。

所以 \(F(w_n^{-k})=nc_k\)。

类似 DFT，把 \(w_n^0,w_n^{-1},\dots,w_n^{1-n}\) 带入 \(F\) 求值，我们只需要再 \(O(n)\) 计算 \(c_k=\dfrac{F(w_n^{-k})}{n}\) 就可以得到目标多项式。

时间复杂度 \(T(n)=O(n\log n)\)。

Part 4. 总结

综上，我们通过 DFT 和 IDFT 完成了 \(O(n\log n)\) 计算多项式乘法。