林学长讲课笔记
极限
\(\lim_{x \to x_0} f(x)\)
考虑运算法则:
- 一般来说,函数的和差商积的极限等于函数的极限的和差商积。
但是例外:
\[\lim_{x \to 3} \frac {x - 3}{x^2 - 9} \]考虑极限约去 \(x - 3\) 得到:
\[\lim_{x \to 3} \frac 1 {x + 3} = \frac 16 \]如果约不掉?但是……
\[\lim_{x \to 1} \frac {2x - 3} {x^2 - 1} \]考虑 \(2x - 3\) 不为 \(0\),所以 \(= \infty\)
总结到一般的高次多项式?
\[\lim_{x \to \infty} \frac {a_0 x^m + \cdots}{b_0 x^n + \cdots} \]-
若 \(m > n\) 则 \(= \infty\)
-
若 \(m = n\) 则 \(= \frac {a_0}{b_0}\)
-
若 \(m < n\) 则 \(= 0\)
发散?收敛?看是否存在可数的上下界
\[\lim_{x \to \infty} \frac {\sin x} x \]考虑 \(\lim \frac 1x = 0\),而 \(\sin x\) 是有界函数,故 \(\lim \frac {\sin x} x = 0\)(\(0\) 乘上一个有界函数)
重要的极限:
\[\lim_{x \to 0} \frac {\sin x} x = 1 \tag{1} \]\[\lim_{x \to \infty}(1 + \frac 1 x)^x = e \tag{2} \]可以利用夹逼定理证明 \((1)\)。考虑:
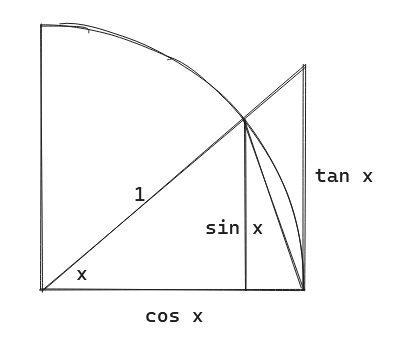
发现三个面积有:
\[\frac 12 \sin x \le \frac 12 x \le \frac 12 \tan x \]整理一下:
\[1 \le \frac x {\sin x} \le \frac 1 {\cos x} \]根据夹逼定理,有 \(\lim \frac x {\sin x} = 1\)。
导数
对于 \(f(x)\),\(f'(x)\) 表示函数在 \(x\) 时的斜率。
\[f'(x) = \lim_{\Delta x \to 0} \frac {f(x + \Delta x) - f(x)}{\Delta x} = \frac {dy} {dx} \]常见的导数:
| \(f(x)\) | \(f'(x)\) |
|---|---|
| \(C\) | \(0\) |
| \(x^\mu\) | \(\mu x ^{\mu - 1}\) |
| \(\sin x\) | \(\cos x\) |
| \(\cos x\) | \(-\sin x\) |
| \(a^x\) | \(a^x \ln a\) |
| \(\log_ax\) | \(\frac 1{x \ln a}\) |
运算法则:
-
\([u(x) \pm v(x)]' = u'(x) \pm v'(x)\)
-
\([u(x)v(x)]' = u(x)v'(x) + u'(x)v(x)\)
-
\([\frac {u(x)}{v(x)}]' = \frac {u'(x)v(x) - u(x)v'(x)}{v^2(x)}\) 这是子导母不导减去母导子不导。
考虑一下常用导数:
\[f(x) = \tan x = \frac {\sin x}{\cos x} = \frac {\cos^2 x + \sin^2 x}{\cos^2 x} = \frac 1 {\cos^2 x} \]对于反函数:
\[f(x) = y \iff f^{-1}(y) = x \]有:
\[[f^{-1}(x)]' = \frac 1 {f'(f(x))} \]于是对于 \(f(x) = \arctan x\),有:
\[\begin{aligned} (\arctan x)' &= \frac 1 {\tan'(\arctan x)} \\ &= \cos^2 (\arctan x) \\ &= \frac 1 {1 + \tan^2 (\arctan x)} \\ &= \frac 1 {1 + x^2} \end{aligned} \]对于复合函数 \(y = f(g(x))\) 求导。
令 \(u = g(x)\),于是 \(\to y = \frac {du}{dy}, u' = g'(x) = \frac {dx}{du}\)。
也就是 \(y' = f'(x) \cdot g'(x)\)。
例如 \(e^{x^3}\) 的导数相当于 \(f(x) = e^x, g(x) = x^3\) 函数复合求导。
于是 \((e^{x^3})' = f'(x)\cdot g'(x) = e^x \cdot 3x^2\)。
柯西中值定理 描述的是:
若在 \([a, b]\) 上 \(f(x), F(x)\) 连续,在 \((a, b)\) 上 \(f(x), F(x)\) 可导且 \(\forall x \in (a, b) F'(x) \ne 0\) 那么一定至少存在一个点 \(\xi\) 使得:
\[\frac {f(a) - f(b)}{F(a) - F(b)} = \frac {f(\xi)}{F(\xi)} \]那么对于洛必达法则:
-
当 \(x \to a\) 时,\(f(x), F(x)\) 都趋近于 \(0\)。
-
\(\lim_{x \to a} \frac {f'(x)}{F'(x)}\) 存在(或为无穷大)
那么:
\[\lim_{x \to a}\frac {f(x)}{F(x)} = \lim_{x \to a} \frac {f'(x)}{F'(x)} \]考虑转化为:
\[\lim_{x \to a}\frac {f(x) - 0}{F(x) - 0} \]如果满足了第一个条件,那么可以依据柯西中值定理构造出:
\[\frac {f(x) - f(a)}{F(x) - F(a)} = \frac {f'(\xi)}{F'(\xi)} \]\(\xi\) 在 \(a, x\) 之间。那么原式成立。
既然洛必达法则存在,那么考虑泰勒展开逼近:
\[f(x) = \sum_{n = 0}^\infty \frac {f^{(n)}}{n!} x^n \]考虑展开 \(\ln(1 + x)\) 有:
\[f^{(n)}(0) = (-1)^{n - 1}(n - 1)! \]于是
\[\begin{aligned} \ln(1 + x) &= x - \frac {x^2} 2 + \frac {x^3} 3 - \frac {x ^ 4} 4 + \cdots \\ &= \sum_{n = 1}^{\infty} \frac {(-1)^{n - 1}}n x^n \end{aligned} \]勾股数组定理
对于每一个本原勾股数组 \((a, b, c)\),都可以从如下公式推出:
\[a = st, b = \frac {s^2 - t^2} 2, c = \frac {s^2 + t^2} 2 \]本原勾股数组:满足 \(\gcd(a, b, c) = 1\) 且 \(a^2 +b^2 = c^2\) 的数组。
特别的,如果取 \(t = 1\),那么可以得到三元组:
\[(s, \frac {s^2 - 1}2, \frac {s^2 + 1} 2) \]欧拉函数
对于 \(\varphi(x)\):
-
基于概率的证明
-
基于积性函数的证明
考虑 \(\Z_p\) 的完全剩余系的大小,即是 \(\varphi(p)\)。
Fib 数列周期性
对于 \(f: \Z_n\),记其循环长度为 \(N(n)\)。
可以有:
\[\gcd(x, y) = 1 \implies N(x y) = \mathit{lcm}(N(x)N(y)) \]也可以有:
\[N(p^k) = p^{k - 1}N(p) \]那么现在的问题是 \(N(p)\),观察可知:
\[N(p) = \begin{cases} p - 1, p \equiv 1 \pmod {10} \\ \end{cases} \]-
\(p \equiv \pm 1 \pmod {10} \implies N(p) | p - 1\)
-
\(p \not\equiv \pm 1 \pmod {10} ~and~ p \not\equiv 5 \pmod {10} \implies N(p) | 2p + 2\)
-
\(\cdots\)
但是考虑有点小小的刻意,所以考虑 \(\bmod 5\)。
\[N(p) | \begin{cases} p - 1, p \equiv \pm 1 \pmod 5 \\ 2p + 2, p \equiv \pm 2 \pmod 5 \\ \end{cases} \]特殊的 \(N(5) = 20\)。
特殊的等式:
- \(f_{n-1}^2 + f^{2}_{n+1} = f_{2n}\)
佩尔方程
\[x^2 - Dy^2 = 1 \]可以如下解:
\[\begin{aligned} (x + \sqrt D y) (x - \sqrt D y) = 1 \\ (x^2 + Dy^2 + 2\sqrt D x y)(x^2 + Dy^2 - 2\sqrt D x y) = 1 \\ (x^2 + Dy^2) - 4D x^2y^2 = 1 \\ (x^2 + Dy^2) - D (2xy)^2 = 1 \end{aligned} \]于是如果可以解出一组 \((x, y)\),那么可以构造 \((x^2 + Dy^2, 2xy)\) 作为新的解。
丢番图逼近
\[x^2 - Dy^2 = k \]连分数
\[\frac {p_n}{q_n} = a_0 + \cfrac {1} {a_1+ \cfrac {1} {a_2 + \cfrac {1} {\ddots + \cfrac 1 {a_n}}}} \]可以简单记为一个序列 \([a_0, a_1, a_2, \cdots ]\)。
连分数递推公式,用于求解 \(p_n, q_n\)。
\[p_0 = a_0, p_1 = a_0 a_1 + 1 \\ q_0 = 1, q_1 = a_1 \]有:
\[\begin{aligned} p_n = a_n p_{n - 1} + p_{n - 2} \\ q_n = a_n q_{n - 1} + q_{n - 2} \end{aligned} \]考虑归纳证明即可。
标签:cos,frac,数论,lim,学长,数学,aligned,sin,equiv From: https://www.cnblogs.com/jeefy/p/17643794.html