会议/期刊: ICML
年份: 2022
1. Vanilla Transformer Block(MHSA+FFN)
原本的Transformer的Block遵循如下的设计范式:MHSA(多头自注意力)+ 一层或者两层的FFN(全连接层),如下图所示。我们只考虑FFN的话,其数学表达式如下:T表示句子长度,d表示词向量维度(也表示模型隐藏层维度),e表示expanded intermediate 特征大小。
\[{\cal O}=\phi(X W_{u})W_{o}\mathrm{~Where~}\,\, X\in\mathbb{R}^{T\times d}, W _{u}\in\mathbb{R}^{d\times e},W_{o}\in\mathbb{R}^{e\times d} \]
2. 改进Transformer Block (MHSA+GLU)
后面有工作对FFN做了改进,提出了GLU(Gated Linear Unit)结构,并且发现能有效提升模型性能。GLU结构大致如下图。简单理解就是有两个支路,两条支路都是全连接层加激活函数。两条支路的激活函数可以不同。最后两路的结果会做element-wise相乘,得到的结果会再经过一个全连接层进行处理。
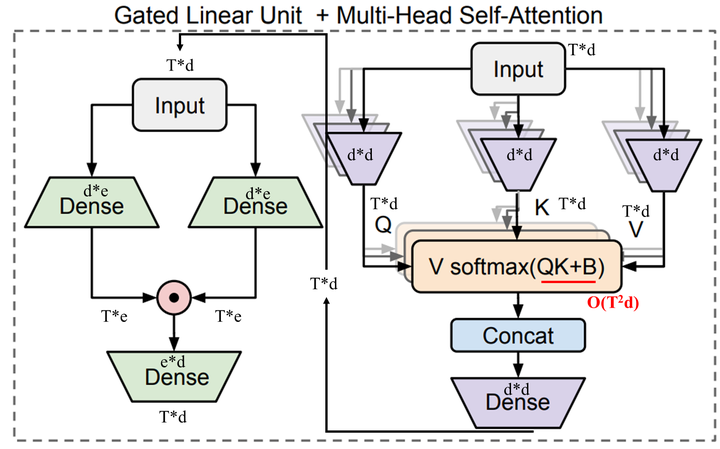
上图左边的GLU结构的数学表达式如下:
\[\begin{array}{l l}{{U=\phi_{u}(X W_{u}),}}&{{V=\phi_{v}(X W_{v})}}\\ {{{O}=\left(U \odot V\right)W_{o}}}\tag{1}\end{array} \]其中\(U,V\in\mathbb{R}^{T\times e},O\in\mathbb{R}^{T\times d}\)
3. GAU(Gated Attention Unit)
上面的GLU和注意力模块是独立开的,GAU做了一个很巧的构思把二者融合到了一个模块,其结构和伪代码如下图所示
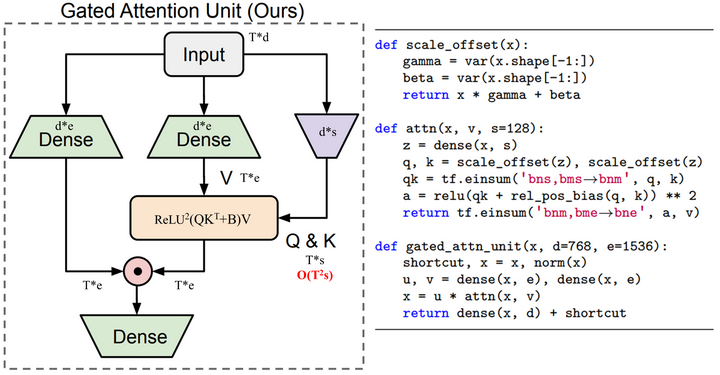
GAU的数学表达式如下:
\[{O}=(U\odot\hat{V})W_{o}\quad\mathrm{where}\quad\hat{V}=A V \tag{2} \]其中
\[\begin{array}{l l}{{Z=\phi_{z}(X W_{z})}}&{{\qquad\in\mathbb{R}^{T\times s} }}\\ {{A=\operatorname{relu}^{2}\left(\mathcal{Q}(Z)\mathcal{K}(Z)^{\top}+b\right)}}&{{\qquad\in\mathbb{R}^{T\times T} }}\tag{3}\end{array} \]可以看到在计算注意力矩阵A用到的Q和K是基于共享的矩阵Z计算得到的,\(\mathcal{Q}(Z), \mathcal{K}(Z)\)都是对矩阵Z做per-dim的归一化,类似于LayerNorm。得到注意力A后,还要经过ReLU激活函数,然后取二次方,即\(relu^2\),这个是在《Primer: Searching for Efficient Transformers for Language Modeling》论文中用NAS搜索出来的。
3.1 参数量比较
下面我们比较一下 MHSA +MLP/GLU与 GAU 结构的参数量:
- MHSA+MLP/GLU
- MHSA: Q, K, V对应的映射模块权重均为hdd/h=dd,最后MHSA的Dense层的权重参数量也是dd,所以MHSA的参数量为4dd
- MLP: 通常是两个全连接层,每个的权重参数量为de,一般e=4d,所以MLP模块的权重参数量为 2 * (de)=2* (d4d)=8d*d
- GLU: 如果采用GLU结构,那么权重参数量则为3de=12dd
- 总结:如果采用MHSA+MLP,则参数量是12dd;如果采用MHSA+GLU,则参数量是16dd
- GAU参数量为3de+ds。通常s会远远小于d,所以参数量近似为3de。改论文中,作者设置e=2d,那么GAU模块的参数量则为6d*d。换言之两个GAU级联后的参数量等价于MHSA+MLP。
3.2 计算复杂度比较
对比GLU+MHSA和GAU,我们可以看到GAU只有一个head,而且去掉了Softmax,而且实验结果显示GAU的表现和原来的MHSA+MLP也不分伯仲,甚至更好

但是,仔细分析一下,我们会发现GAU的计算复杂度和原本的自注意力机制一样,仍旧是句子长度的二次方,即\(O(T^2)\)。
下面我们分析一下二次复杂度的来源,GAU和原始的自注意力机制的计算都可以用如下的数学公式表示:
\[A=\phi(QK^T)V \]在原始的自注意力机制中,激活函数\(\phi\)是softmax,而在GAU中是\(ReLU^2\)。矩阵\(Q, K\in\mathbb{R}^{T\times d}\),二者矩阵乘法的复杂度为\(O(T\times d \times T)\),如果只考虑句子长度,我们可以将d忽视,所以复杂度为\(O(T^2)\).
后续的一些尝试将复杂度降低至线性复杂度的方法的思路是这样的,
\[\phi(QK^T)V\rightarrow(\phi_q(Q)\phi_k(K)^T)V=\phi_q(Q)(\phi_k(K)^TV) \]简而言之就是尝试将矩阵\(K^T\)和\(V\)先做矩阵乘法,这样一来它们的复杂度则为\(O(d\times T \times d)\),得到大小为\(\mathbb{R}^{d\times d}\)的矩阵,该矩阵再和\(Q\)相乘,计算复杂度同样是\(O(d\times T \times d)\)。
3.3 推理阶段的复杂度
我们接下来考虑推理时GAU的复杂度。
我们知道GAU会先算\(M=K^TV\),然后再计算\(QM\),所以我们先着重分析一下矩阵\(M\)的计算。
由于推理阶段采用的是自回归的解码方式,也就是说K和V的长度(即词数量)是从1逐渐增加到T的。考虑t时刻的情况,要得到矩阵\(M_t\), 我们需要\(O(d*t*d)\)的计算复杂度,随着t逐渐从1增加到T,计算复杂度是不断增加的,换言之计算复杂度是\(O(Td^2)\)。
这里其实有一个计算上的技巧,即我们需要先存储上一次的结果\(M_{t-1}\)。当到t时刻的时候,我们计算出新词的\(K_t,V_t\in\mathbb{R}^{1\times d}\)向量,然后计算\(K_t^TV_t\in\mathbb{R}^{d\times d}\),最后将这个值和\(M_{t-1}\)累加即可得到\(M_t\),即
\[M_t=M_{t-1}+K_t^TV_t \tag{4} \]简而言之,每个时刻(即有新的词输入的时候),只需要计算新词的\(K_t^TV_t\)即可,因此空间复杂度是\(O(d^2)\),计算复杂度始终保持为\(O(d^2)\),相比于原来的\(O(Td^2)\)计算复杂度有了明显改进。
上述这种计算技巧在推理阶段非常有效,可以很巧妙地降低计算复杂度。但是,在训练阶段就会有问题了,因为这个技巧是基于自回归的特点设计的,也就是说推理阶段就像RNN一样,每次只新增一个单词,无需考虑并行性。训练阶段输入的数据一般是大小为\(b\times T\times d\)的张量,如果想采用上面的计算技巧,那么训练阶段的输入就需要像推理阶段一样,显然这会得不偿失,因为这样无法并行计算了。
4. Mixed Chunk Attention
为了解决上面提到的推理计算技巧无法应用到训练阶段,本文作者提出了Mixed Chunk Attention方法,该方法将Partial Attention(简单理解就是只计算更重要部分的注意力,但是实际上这类方法的计算效率不高,因为计算是不规则和碎片化的)和Linear Attention的优点进行了结合。
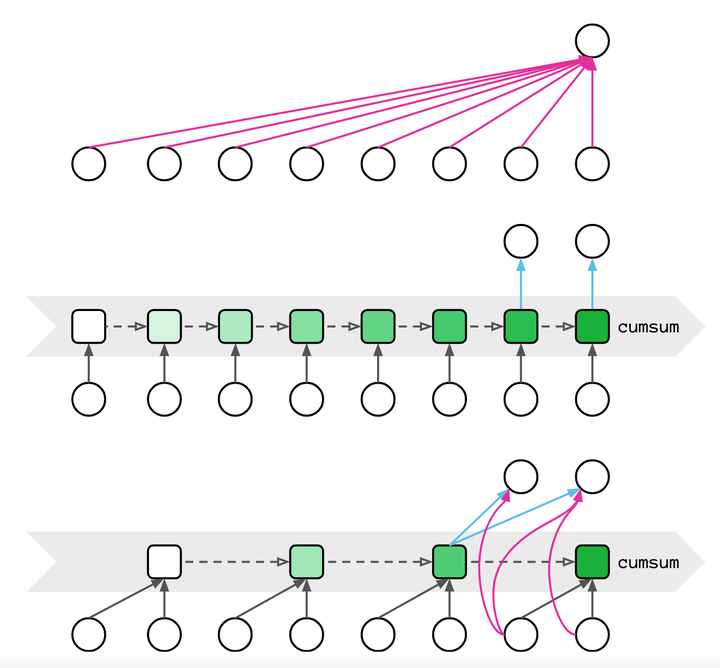
上面图中每个圆圈代表一个单词的词向量,中间的正方形表示\(M_t=M_{t-1}+K_t^TV_t\)。
图(top)表示原始的注意力机制计算方法,每次计算注意力矩阵的复杂度是\(O(T^2d)\)。
图(middle)即表示通过公式(4)可以复用前一时刻的结果,将计算复杂度降低至\(O(d^2)\),但是在这种类似RNN的计算方式缺乏并行性,很难在训练阶段使用
图(bottom)则做了这种,所以称作mixed chunk attention (MCA)。假设输入序列维度是\(b\times T\times d\),后面为避免符号太多,我们省略batch size,即\(b\)。由图(bottom)可以看到,MCA其实就是将原来的一个句子划分成\(G\)个chunk,每个chunk包含\(C\)个单词(该论文取\(C=256\)),也就是说原来的句子长度\(T=G\times C\)。所以原本的输入序列\(T\times d\rightarrow G\times C\times d\)。原本的GAU模块转变成了如下图:
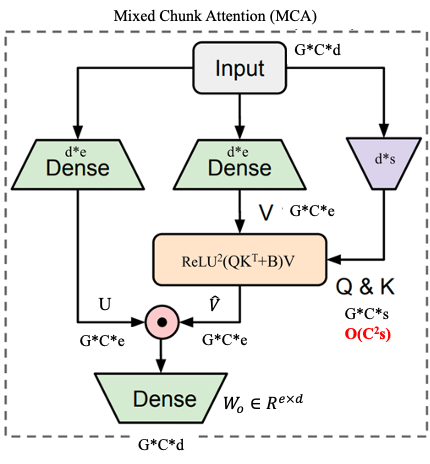
为方便理解,我们只考虑单个chunk,那么对于第\(g\)个chunk,则中间结果\(U_g\in\mathbb{R}^{C\times e},V_g\in\mathbb{R}^{C\times e},Z_g\in\mathbb{R}^{C\times s},\)其中Q,K矩阵是基于共享的\(Z_g\)采用不同的放射变化得到的,具体而言会有两套Q,K矩阵:
- 一套用于计算local Attention的复杂度为二次方的\(Q_g^{quad},K_g^{quad}\in\mathbb{R}^{C\times s}\)。如图5(bottom)最下面那一行圆圈所示,每两个圆圈之间会计算彼此之间的注意力矩阵,这其实可以理解成一种稀疏的注意力,其计算公式如下
单个chunk的local Attention的计算中的\(Q_g^{quad}K_g^{quad}\)计算复杂度为\(O(C^2s)\),计算得到的结果与矩阵\(V_g\)相乘的计算复杂度为\(O(C^2e)\),因为\(s<<d\),另外\(e\)正比于\(d\)(例如\(e=2d\)),所以复杂度是\(O(C^2s+C^2e)=O(C^2s+2C^2d)=O(C^2d)\)。另外由于总共有G个chunk,所以总的复杂度为\(O(GC^2d)=O(TCd)\)
- 另一套是用于计算global Attention的复杂度为线性的\(Q_g^{lin},K_g^{lin}\in\mathbb{R}^{C\times s}\)。我们其实可以将图5(bottom)最下面每两个圆圈视为一个圆圈,就像图5(middle)一样。此时计算global Attention可以分成两种情况:训练和推理,或者也可以称作Non-Causal和Causal。Causal表示因果,即下一个单词的预测依赖前面的输入,这就对应推理。两种情况的具体计算公式如下:
- Non-Causal (训练):
训练阶段其实可以不用像公式(6)那样分chunk的去计算,我们其实可以直接用完整的矩阵\(Q^{lin},K^{lin}\in\mathbb{R}^{T\times s}\)直接计算得到公式(6)右边的累加项。
我们再看看计算复杂度,\({K_h^{lin}}^TV_h\)的计算复杂度为\(O(Cse)\),累加G个chunk,那么复杂度就是\(O(GCse)=O(Tse)=O(Tsd)\)。矩阵Q与KV计算的到矩阵相乘的复杂度为\(O(Cse)=O(Csd)\)。所以公式(6)的计算复杂度近似为\(O(Tsd)\)。
- Causal (推理):
根据两套Q,K矩阵,我们可以分别求得\(\hat{V}_g^{quad},\hat{V}_g^{lin}\),最后我们将二者相加得到混合注意力,最终第\(g\)个chunk的输出计算公式如下
\[O_g=[U_g\odot(\hat{V}_g^{quad}+\hat{V}_g^{lin})]W_o \tag{8} \]Mixed Chunk Attention伪代码如下:

5. 论文中的一些讨论
5.1 Chunk是否需要overlap
前面提到将输入序列划分成多干个chunk,这些chunk彼此之间是没有overlap的。比如说这句话“今天我吃了好多好吃的,有龙虾、鲍鱼、海参和饺子。”,以non-overlap的划分方式将这个句子(总共24个字符)划分成三个chunk,则得到
- [今天我吃了好多好]
- [吃的,有龙虾、鲍]
- [鱼、海参和饺子。]
那么,一个很自然的问题是如果overlap会怎么样呢?结果是否会更好?作者对这个做了测试,实验结果表明overlap的划分chunk的方式的确能够提升模型性能,但是引入了额外的计算成本。与其使用overlap 的chunk划分方式,还不如直接多加几层non-overlapping GAU模块。
5.2 局部和全局注意力的Ablation Study
原论文还做了消融实验,显示相对来说局部注意力比全局注意力更重要,而混合式的效果最好。下面实验中的MC-TFM++是指将Mixed Chunk Attention运用到Transformer++。MC-TFM++和FLASH一样都是线性复杂度,但是用的FFN。可以看到使用GAU的FLASH要明显优于MC-TFM++。
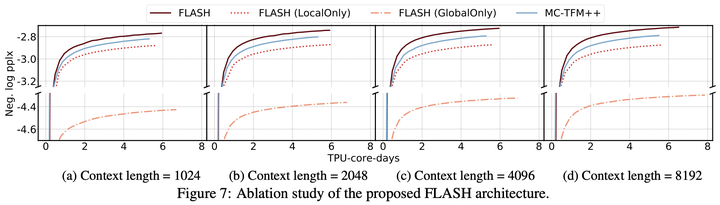
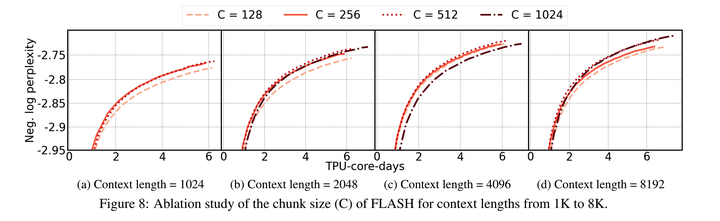
5.3 Chunk大小该如何选择
- 当C和句子长度一样时,此时等价于FLASH-Quad,即计算复杂度为二次方
- 当C=1时,则等价于Linear Attention,但是在做auto-regressive training的时候不够高效,缺少并行性
- 下图给出了在不同句子长度下,C取不同值「128, 256, 512, 1024」的效果,彼此差距不是很大,最终作者选取了256