题目
先放板子:
求 \(\sum\limits_{x=1}^{L}{A^xB^{\lfloor \frac{Px+R}{Q} \rfloor}}\),其中 \(L,P,Q,R \leq 10^{18}\)
现在看来这个问题比较棘手,不过我们可以先从一些简单的东西入手。
思想
考虑这样一条直线 \(y=\frac{Px+R}{Q}(0 \leq R < Q)\),将它在平面直角坐标系中画出来,可以看见它会穿过若干个格子:
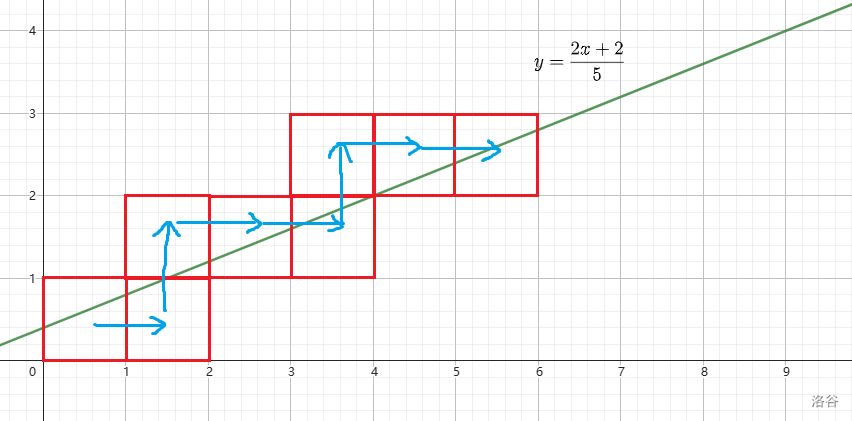
如上图就是 \(y=\frac{2x+2}{5}\) 的例子。我们将格子向右延伸称作 \(R\),向上延伸称作 \(U\),若直线碰到格点,则视作先向上再向右,则在这条直线上的格子延伸情况即为 \(\text{RURRURRRUR}\dots\)
不难发现,这个字符序列满足在第 \(x\) 个 \(\text{R}\) 前,有恰好 \(\lfloor \frac{2x+2}{5} \rfloor\) 个 \(\text{U}\) 在它前面,根据定义不难证明。
推广到一般函数,我们可以得到这个序列的又一个定义,即:满足第 \(x\) 个 \(\text{R}\) 前恰好有 \(\lfloor \frac{Px+R}{Q} \rfloor\) 个 \(\text{U}\) 的序列。这个定义能够帮助我们更理性地对待以后的问题,而不是在坐标系上随便画画感性理解。
现在的问题就是,如何求 \(x \leq L\) 时的序列?
换句话说,假设 \(\text{U}\) 和 \(\text{R}\) 都是一个支持合并的信息(有结合律但不一定有交换律),我们想要求出这个序列最终的值,其中这个序列满足上面的定义,有恰好 \(L\) 个 \(\text{R}\),且最后一个操作就是 \(\text{R}\)。
以下分两种情况讨论:
- \(P \geq Q\)
不妨设 \(P=kQ+P'(0 \leq P' < Q)\),根据定义,可以得到第 \(x\) 个和 第 \(x-1\) 个 \(\text{R}\) 之间 \(\text{U}\) 的个数为:
\[\lfloor \frac{Px+R}{Q} \rfloor-\lfloor \frac{P(x-1)+R}{Q} \rfloor \]\[=\lfloor \frac{P'x+R}{Q} \rfloor+kx-\lfloor \frac{P'(x-1)+R}{Q} \rfloor-k(x-1) \]\[=\lfloor \frac{P'x+R}{Q} \rfloor-\lfloor \frac{P'(x-1)+R}{Q} \rfloor+k \]这就相当于在 \(y=\frac{P'x+R}{Q}\) 的基础上,每一段 \(\text{U}\) 后面都额外补上 \(k\) 个 \(\text{U}\)。直接令 \(P \leftarrow P',\text{R} \leftarrow \text{U}^k\text{R}\) 即可。
- \(P<Q\)
这部分比较繁琐,我们希望交换 \(P\) 和 \(Q\) 的地位来继续递归下去。根据第 \(x\) 个 \(\text{R}\) 前有 \(\lfloor \frac{Px+R}{Q} \rfloor\) 个 \(\text{U}\),我们可以知道第 \(x\) 个 \(\text{U}\) 前有多少个 \(\text{R}\)。具体地,可以列出式子:
\[\lfloor \frac{Pi+R}{Q} \rfloor < x \]\[\frac{Pi+R}{Q} < x \]\[i < \frac{Qx-R}{P} \]\[i < \lceil \frac{Qx-R}{P} \rceil \]\[i \leq \lceil \frac{Qx-R-P}{P} \rceil \]\[i \leq \lfloor \frac{Qx-R-1}{P} \rfloor \]但是,这还不满足我们前面提到的序列定义的要求。
第一点,\(-R-1 \notin [0,P)\),根据定义理解,就是第 \(0\) 个 \(\text{U}\) 前理应有 \(0\) 个 \(\text{R}\),但这里有 \(\lfloor \frac{-R-1}{P} \rfloor\) 个,竟然是个负数!所以我们可以把第一个 \(\text{U}\) 前面的部分截掉单独处理,后面就能满足要求了。第一个 \(\text{U}\) 前面有 \(\lfloor \frac{Q-R-1}{P} \rfloor\) 个 \(\text{R}\),所以前面先乘上 \(\text{R}^{\lfloor \frac{Q-R-1}{P} \rfloor}\text{U}\)。至于后面,第 \(i+1\) 个 \(\text{U}\) 变成了第 \(i\) 个 \(\text{U}\),所以现在的函数变成了 \(y=\frac{Qx+Q-R-1}{P}\),又因为前面 \(\lfloor \frac{Q-R-1}{P} \rfloor\) 个 \(\text{R}\) 被截掉了,所以所有 \(\text{U}\) 前面 \(\text{R}\) 的个数都应该减掉 \(\lfloor \frac{Q-R-1}{P} \rfloor\),原函数就变成了 \(y=\frac{Qx+Q-R-1}{P}-\lfloor \frac{Q-R-1}{P} \rfloor=\frac{Qx+(Q-R-1)\%P}{P}\)。
第二点,\(L\) 的限制怎么办,我们希望转换后最后一个操作是 \(\text{U}\),才能继续递归下去。我们知道总共有 \(m=\lfloor \frac{PL+R}{Q} \rfloor\) 个 \(\text{U}\),所以可以将第 \(m\) 个 \(\text{U}\) 后面的 \(L-\lfloor \frac{Qm-R-1}{P} \rfloor\) 个 \(\text{R}\) 单独处理,即最后再乘上 \(\text{R}^{L-\lfloor \frac{Qm-R-1}{P} \rfloor}\)。注意 \(m=0\) 要特判。
经过掐头去尾的操作后,我们成功将 \(P,Q\) 和 \(\text{U},\text{R}\) 交换地位了,继续递归下去即可。边界即为 \(L=0\)。
核心代码
node solve(ll P,ll Q,ll R,ll L,node A,node B){
if(!L) return I;
if(P>=Q) return solve(P%Q,Q,R,L,A,mpow(A,P/Q)*B);
ll m=((__int128)P*L+R)/Q;
if(!m) return mpow(B,L);
return mpow(B,(Q-R-1)/P)*A*solve(Q,P,(Q-R-1)%P,m-1,B,A)*mpow(B,L-((__int128)Q*m-R-1)/P);
}
其中的 \(A\) 就是 \(\text{U}\),\(B\) 就是 \(\text{R}\),\(I\) 是单位元。
那会这玩意要怎么过上面的模板题呢?容易发现题目的 \(A\) 就很像我们的 \(\text{R}\),\(B\) 就很像我们的 \(\text{U}\)。
于是设三元组 \((cntA,cntB,ans)\) 表示目前这个序列有多少个 \(\text{R}\),多少个 \(\text{U}\),以及答案是什么。
合并就是 \((cntA_1,cntB_1,ans_1)\times (cntA_2,cntB_2,ans_2) = (cntA_1+cntA_2,cntB_1+cntB_2,ans_1+A^{cntA_1}ans_2B^{cntB_1})\)。
显然记 \(cntA,cntB\) 不如记 \(A^{cntA},B^{cntB}\),于是复杂度为 \(\mathcal O(n^3\log\max(P,Q))\),\(n^3\) 为矩阵乘法的复杂度。
由上述过程可以看出,我们只需要将 \(\text{U}\) 和 \(\text{R}\) 根据题目赋上符合要求的信息,之后无脑套板子就行了,这就是它相比类欧的优势之处。