斜率优化dp
引入
首先,我们考虑一种更简单的dp优化——单调队列优化。
比如,一个dp式形如:
\[dp_{i} = \min_{k \leq j \leq i} (dp_j+f_j+g_i) \]我们发现,这个式子可以通过拆分(wgj:分离变量),变形成如下式子:
\[dp_{i} = \min_{k \leq j \leq i} (dp_j+f_j)+g_i \]怎么样?我们发现,取最小值的这一项只与 \(j\) 有关,其余项只与 \(i\) 有关,那么我们可以想办法搞出 \(dp_j+f_j\) 的最小值,然后直接转移即可。我们发现,\(j\) 是在一个区间内的,那取最小值就转化为一个滑动窗口问题,使用单调队列即可。
总结一下,如果dp式中的元素可以分类,即一部分只与 \(i\) 有关,另一部分只与 \(j\) 有关,并且 \(j\) 有区间范围,区间单调右移,这样的dp就可以采用单调队列优化掉一层枚举。
但是,有时候,dp式子中的某一项既与 \(i\) 有关,又与 \(j\) 有关,例如以下dp式:
\[dp_i = \min_{0 \leq j < i}(dp_j+a_j+b_ic_j) \]这时候你就完蛋了你就会痛苦的发现,单调队列不太行xwx。因为对于这个函数,我们很难直接找出最优决策点。
这时候,我们引入斜率优化。
斜率优化
Part 1:推式子
我们就题来谈 [APIO2010] 特别行动队
首先,这个题的dp式子很显然。我们设 \(s\) 为 \(x\) 的前缀和数组,\(dp_i\) 表示到第 \(i\) 个人,分组后的最大和,那么有:
\[dp_i = \max(dp_j+a(s_i-s_j)^2+b(s_i-s_j)+c) \]然后,我们对它进行化简:
\[dp_i = \max (dp_j+as_j^2-bs_j-2as_is_j)+as_i^2+bs_i+c \]关于 \(i\) 的部分,我们可以当作常量提出去,令这部分为 \(g_i\);剩下的部分中,一部分只与 \(j\) 有关,我们令这部分为 \(f_j\),这样,式子变为:
\[dp_i = \max(f_j-2as_is_j)+g_i \]这时候,我们来看一下 \(\max\) 内部的部分。我们不妨设 \(f_1-2as_is_1 \leq f_2 -2as_is_2\),那么经过移项,有:
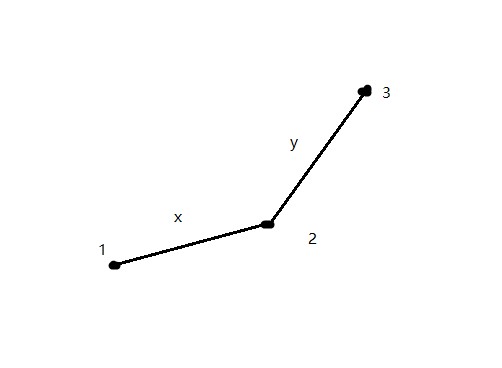
\[\frac{f_2-f_1}{s_2-s_1} \geq 2as_i \]这样子,我们会发现一些内幕。如果平面直角坐标系中有两个点 \(A(s_1, f_1)\),\(B(s_2, f_2)\),那么上述式子等价于过 \(A\) 和 \(B\) 两点的直线的斜率。
Part 2:合法点集斜率单调性
我们总结一下上一个部分的结论:如果两个点连线的斜率不小于 \(2as_i\),那么前面这个点对应的 \(j\) 就不是最优决策点;反之,后者对应的 \(j\) 不是最优决策点。
我们考虑三个点的简化情况,假设 \(1\) 号点到 \(2\) 号点的斜率为 \(x\),\(2\) 号到 \(3\) 号点斜率为 \(y\),令 \(x<y\),\(k = 2as_i\):
我们发现,\(2\) 号点一定不是最优决策点。因为它为最优点的充要条件是 \(y < k\) 并且 \(x \geq k\),而 \(x < y\)。
那么,我们就可以宣:\(2\) 号点你废了!抹(ma)走!
扩展一下:如果我们现在有很多个点,而这个点集中,如果存在三个横坐标递增的点,使得前两个点的斜率小于等于后两个点的斜率,那么可以删掉中间的点。
所以,如果我们处理出一个不可删点集的斜率数组(也就是最终要挑选出最优决策点的点集),那这个数组必然是单调递减的。
Part 3 找最优决策点
那这样,我们就可以二分来查找最优决策点。
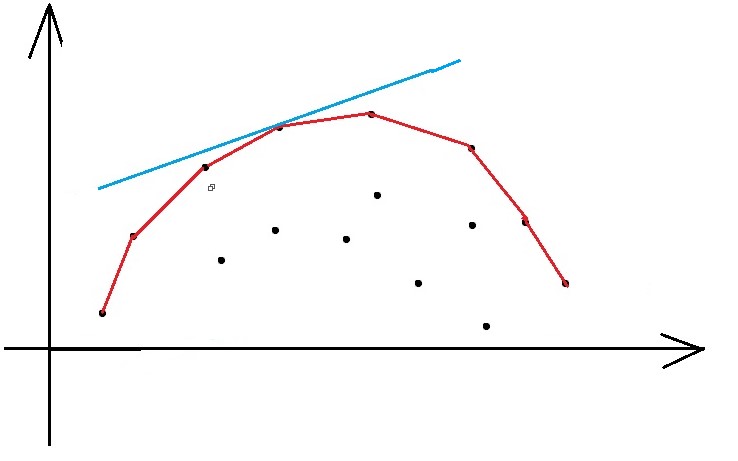
其实,如果我们画图来看,会发现上述过程中,我们维护了一个凸壳;
而找最优决策点,实际上就是令一条斜率为 \(k\) 的直线去切这个凸壳,切点即为最优决策点。
Part 4 代码实现
在这道题中,可以省略二分这一步。为什么呢?因为这道题的 \(k\) 是单调递减的,所以我们每次只需要把队头斜率斜率比 \(2as_i\) 大的弹走,留下的队头就是最优决策点。
至于在队尾加入元素,我们维护上凸包,每次比较队尾的两个元素的斜率和队尾与 \(i\) 点的斜率,如果后者大于前者,就弹队尾。
注意有些细节:求斜率必须要有两个点,所以要初始化队列头尾指针为 \(0\),这样当队列为空时,能保证队列中仍存在一个点。
#include<bits/stdc++.h>
#define LD long double
#define ll long long
using namespace std;
const int N = 1e6+100;
inline ll read(){
ll x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9'){
if(ch == '-') f = -1;
ch = getchar();
}
while(ch>='0'&& ch<='9'){
x = x*10+ch-48;
ch = getchar();
}
return x * f;
}
int n, L;
ll s[N];
ll a, b, c;
ll dp[N];
LD q[N];
int lq , rq;
LD getx(int x){
return s[x];
}
LD gety(int x){
return a*s[x]*s[x]-b*s[x]+dp[x];
}
LD getk(int x, int y){
return (gety(y)-gety(x))/(getx(y)-getx(x));
}
int main(){
scanf("%d", &n);
scanf("%lld%lld%lld", &a, &b, &c);
for(int i = 1; i<=n; ++i){
s[i] = read();
s[i]+=s[i-1];
}
for(int i = 1; i<=n; ++i){
while(lq<rq&&2*s[i]*a<=getk(q[lq], q[lq+1])) lq++;
int j = q[lq];
dp[i] = dp[j]+a*(s[i]-s[j])*(s[i]-s[j])+b*(s[i]-s[j])+c;
while(lq<rq&&getk(q[rq-1], q[rq])<=getk(q[rq], i)) rq--;
q[++rq] = i;
}
printf("%lld\n", dp[n]);
return 0;
}