知识剖析
空间向量的概念
在空间,我们把具有大小和方向的量叫做空间向量,用字母\(\vec{a}, \vec{b}, \vec{c} \ldots \ldots\)表示,空间向量的大小叫做空间向量的长度或模.
解释
\((1)\)空间中点的位移、物体运动的速度、物体受到的力等都可以用空间向量表示;
\((2)\)向量\(\vec{a}\)的起点是\(A\),终点是\(B\),则向量\(\vec{a}\)也可以记作\(\overrightarrow{A B}\),其模记为\(|\vec{a}|\)或\(|\overrightarrow{A B}|\);
\((3)\)向量一般用有向线段表示 同向等长的有向线段表示同一或相等的向量;
\((4)\)向量具有平移不变性.
\((5)\)在空间,零向量、单位向量、相等向量、反向量与在平面的对应向量一样.
运算
(1) 定义
与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图).

\(\overrightarrow{O A}=\overrightarrow{O B}+\overrightarrow{O C}=\vec{a}+\vec{b}\),\(\overrightarrow{C B}=\overrightarrow{O B}-\overrightarrow{O C}=\vec{a}-\vec{b}\),\(\overrightarrow{O P}=\lambda \vec{a}(\lambda \in R)\)
(2) 运算律
① 加法交换律:\(\vec{a}+\vec{b}=\vec{b}+\vec{a}\);
② 加法结合律:\((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\);
③ 数乘分配律:\(\lambda(\vec{a}+\vec{b})=\lambda \vec{a}+\lambda \vec{b}\);
运算法则:三角形法则、平行四边形法则、平行六面体法则.
解释 平行六面体法则:在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(\overrightarrow{A C_{1}}=\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\).

共线向量
(1) 概念
如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共线向量或平行向量,\(\vec{a}\)平行于\(\vec{b}\) ,记作\(\vec{a} / / \vec{b}\).
(2) 共线向量定理
空间任意两个向量\(\vec{a}\) ,\(\vec{b}\)\((\vec{b} \neq \overrightarrow{0})\) ,\(\vec{a} / / \vec{b} \Rightarrow\) 存在实数\(λ\),使\(\vec{a}=\lambda \vec{b}\).
(3) 三点共线
\(A\)、\(B\)、\(C\)三点共线\(\Rightarrow \overrightarrow{A B}=\lambda \overrightarrow{A C} \Rightarrow \overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B}\)(其中 \(x+y=1\))
(4) 与\(\vec{a}\)共线的单位向量为\(\pm \dfrac{\vec{a}}{|\vec{a}|}\) .
共面向量
(1) 定义
一般地,能平移到同一平面内的向量叫做共面向量.说明:空间任意的两向量都是共面的.
(2) 共面向量定理
如果两个向量\(\vec{a}\) ,\(\vec{b}\) 不共线,\(\vec{p}\)与向量\(\vec{a}\) ,\(\vec{b}\) 共面的条件是存在实数\(x\) ,\(y\),使\(\vec{p}=x \vec{a}+y \vec{b}\).
(3) 四点共面
若\(A\)、\(B\)、\(C\)、\(P\)四点共面
\(\Rightarrow \overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A C} \Rightarrow \overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\) (其中\(x+y+z=1\))
方法1 若要证明\(A\)、\(B\)、\(C\)、\(P\)四点共面,只需要证明 \(\overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A C}\)
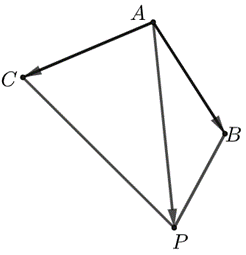
方法2 若要证明\(A\)、\(B\)、\(C\)、\(P\)四点共面,只需要证明\(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}\) (其中\(x+y+z=1\))
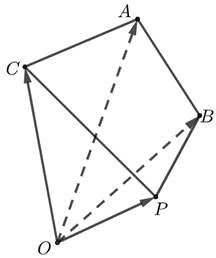
证明 若\(x+y+z=1\),
则 \(\overrightarrow{O P}=x \overrightarrow{O A}+y \overrightarrow{O B}+z \overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B}+(1-x-y) \overrightarrow{O C}\)
\(=\overrightarrow{O C}+x(\overrightarrow{O A}-\overrightarrow{O C})+y(\overrightarrow{O B}-\overrightarrow{O C})=\overrightarrow{O C}+x \overrightarrow{C A}+y \overrightarrow{C B}\),
\(\therefore \overrightarrow{O P}-\overrightarrow{O C}=x \overrightarrow{C A}+y \overrightarrow{C B}\), \(\therefore \overrightarrow{C P}=x \overrightarrow{C A}+y \overrightarrow{C B}\),
即 \(\overrightarrow{C P}\), \(\overrightarrow{C A}\), \(\overrightarrow{C B}\)共面,即\(A\)、\(B\)、\(C\)、\(P\)四点共面.
经典例题
【题型一】空间向量的线性运算
【典题1】 如图所示,在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)为\(A_1 C_1\)与\(B_1 D_1\)的交点,若\(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{A D}=\vec{b}\),\(\overrightarrow{A A_{1}}=\vec{c}\),则\(\overrightarrow{C M}=\)( )

A.\(\dfrac{1}{2} \vec{a}+\dfrac{1}{2} \vec{b}+\vec{c}\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}+\vec{c}\)
C.\(-\dfrac{1}{2} \vec{a}+\dfrac{1}{2} \vec{b}+\vec{c}\) \(\qquad \qquad \qquad \qquad\) D.\(-\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}+\vec{c}\)
【解析】 (与平面向量的方法类似,用“首尾相接法”把\(\overrightarrow{C M}\)向\(\vec{a}, \vec{b}, \vec{c}\)靠拢)
\(\overrightarrow{C M}=\overrightarrow{C B}+\overrightarrow{B M}\)
\(=-\vec{b}+\overrightarrow{B A}+\overrightarrow{A M}\)
\(=-\vec{b}-\vec{a}+\overrightarrow{A A_{1}}+\overrightarrow{A_{1} M}\)
\(=-\vec{b}-\vec{a}+\vec{c}+\dfrac{1}{2} \overrightarrow{A C}\)
\(=-\vec{b}-\vec{a}+\vec{c}+\dfrac{1}{2}(\vec{b}+\vec{a})\)
\(=-\dfrac{1}{2} \vec{a}-\dfrac{1}{2} \vec{b}+\vec{c}\);
故选:\(D\).
【点拨】
① 空间向量运算符合三角形法则、平行四边形法则,类似平面向量;
② 本题解法很多,比较灵活,而本题解题思路是“首尾相接法”:以\(\vec{a}, \vec{b}, \vec{c}\)为基底,在对\(\overrightarrow{C M}\)“首尾相接”的时候,尽量向三个基底靠拢(利用\(\vec{a}, \vec{b}, \vec{c}\)或其共线向量表示),做到最后的式子只含三个基底向量;
③ 类似题目需要大胆下笔推算,也可利用一些常见结论:
(1) 在三角形\(∆ABC\)中,点\(D\)是\(BC\)的中点,则\(\overrightarrow{A D}=\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}\).
(2) 平行六面体法则:在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(\overrightarrow{A C_{1}}=\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\).
【典题2】 已知在空间四边形\(ABCD\)中,\(G\)是\(△BCD\)的重心,\(E\),\(F\),\(H\)分别为边\(CD\),\(AD\)和\(BC\)的中点,化简下列各表达式,并标出化简结果的向量.
(1)\(\overrightarrow{A G}+\dfrac{1}{3} \overrightarrow{B E}+\dfrac{1}{2} \overrightarrow{C A}\);\(\qquad \qquad\) (2) \(\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{A C}-\overrightarrow{A D})\);\(\qquad \qquad\) (3) \(\dfrac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})\)

【解析】 (1) \(\overrightarrow{A G}+\dfrac{1}{3} \overrightarrow{B E}+\dfrac{1}{2} \overrightarrow{C A}=\overrightarrow{A B}+\overrightarrow{B G}+\dfrac{1}{3} \overrightarrow{B E}+\dfrac{1}{2} \overrightarrow{C A}\)
\(=\overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{B E}+\dfrac{1}{3} \overrightarrow{B E}+\dfrac{1}{2} \overrightarrow{C A}=\overrightarrow{A B}+\overrightarrow{B E}+\dfrac{1}{2} \overrightarrow{C A}=\overrightarrow{A E}+\dfrac{1}{2} \overrightarrow{C A}\)
\(=\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{2} \overrightarrow{A D}+\dfrac{1}{2} \overrightarrow{C A}=\dfrac{1}{2} \overrightarrow{A D}=\overrightarrow{A F}\),
(2)\(\dfrac{1}{2}(\overrightarrow{A B}+\overrightarrow{A C}-\overrightarrow{A D})=\overrightarrow{A H}-\dfrac{1}{2} \overrightarrow{A D}=\overrightarrow{A H}-\overrightarrow{A F}=\overrightarrow{F H}\);
(3) \(\dfrac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})=\dfrac{1}{3} \times 2 \overrightarrow{A H}+\dfrac{1}{3} \overrightarrow{A D}=\dfrac{2}{3}\left(\overrightarrow{A H}+\dfrac{1}{2} \overrightarrow{A D}\right)\),
在三角形\(ADH\)中, \(\overrightarrow{D G}=2 \overrightarrow{G H}\),
则 \(\overrightarrow{A G}-\overrightarrow{A D}=2(\overrightarrow{A H}-\overrightarrow{A G})\),
即有 \(\overrightarrow{A G}=\dfrac{1}{3}(2 \overrightarrow{A H}+\overrightarrow{A D})\),则有 \(\dfrac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})=\overrightarrow{A G}\).
巩固练习
1(★) 在四面体\(ABCD\)中,点\(F\)在\(AD\)上,且\(AF=2FD\),\(E\)为\(BC\)中点,则\(\overrightarrow{E F}\)等于\(\underline{\quad \quad}\) (用\(\overrightarrow{A B}\),\(\overrightarrow{A C}\),\(\overrightarrow{A D}\)表示)

2(★) 在空间四边形\(ABCD\)中,连结\(AC\),\(BD\).若\(△BCD\)是正三角形,且\(E\)为其中心,则\(\overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{BC}-\dfrac{3}{2} \overrightarrow{DE}-\overrightarrow{A D}\)的化简结果为\(\underline{\quad \quad}\) .
3(★★) 如图所示,在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{A D}=\vec{b}\),\(\overrightarrow{A A_{1}}=\vec{c}\),\(M\)是\(D_1 D\)的中点,点\(N\)是\(AC_1\)上的点,且\(\overrightarrow{A N}=\dfrac{1}{3} \overrightarrow{A C_{1}}\),用\(\vec{a}, \vec{b}, \vec{c}\)表示向量\(\overrightarrow{M N}\)的结果是 \(\underline{\quad \quad}\) .

4(★★★) 在三棱锥\(A-BCD\)中,\(P\)为\(△BCD\)内一点,若 \(S_{\triangle P B C}=1\), \(S_{\triangle P C D}=2\),\(S_{\triangle P B D}=3\),则\(\overrightarrow{AP}=\)\(\underline{\quad \quad}\) . (用\(\overrightarrow{A B}\),\(\overrightarrow{A C}\),\(\overrightarrow{A D}\)表示)
参考答案
-
【答案】 \(-\dfrac{1}{2} \overrightarrow{A C}-\dfrac{1}{2} \overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{A D}\)
【解析】 在四面体\(ABCD\)中,点\(F\)在\(AD\)上,且\(AF=2FD\),\(E\)为\(BC\)中点,
所以\(\overrightarrow{E F}=\overrightarrow{A F}-\overrightarrow{A E}=\dfrac{2}{3} \overrightarrow{A D}-\left(\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}\right)\)\(=-\dfrac{1}{2} \overrightarrow{A C}-\dfrac{1}{2} \overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{A D}\). -
【答案】 \(\overrightarrow{0}\)
【解析】 如图,延长\(DE\)交\(BC\)于点\(F\),根据题意知\(F\)为\(BC\)的中点.

又因为\(E\)为正三角形\(BCD\)的中心,
所以\(\overrightarrow{DE}=\dfrac{2}{3}\overrightarrow{DF}\),即\(\overrightarrow{DF}=\dfrac{3}{2} \overrightarrow{DE}\),
所以\(\overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{BC}-\dfrac{3}{2} \overrightarrow{DE}-\overrightarrow{A D}=(\overrightarrow{A B}-\overrightarrow{A D})+\overrightarrow{BF}-\dfrac{3}{2} \overrightarrow{DE}\)\(=\overrightarrow{DB}+\overrightarrow{BF}-\overrightarrow{DF}=\overrightarrow{DF}-\overrightarrow{DF}=\overrightarrow{0}\). -
【答案】 \(\dfrac{1}{3} \vec{a}-\dfrac{2}{3} \vec{b}-\dfrac{1}{6} \vec{c}\)
【解析】 \(∵M\)是\(D_1 D\)的中点,\(\overrightarrow{A N}=\dfrac{1}{3} \overrightarrow{A C_{1}}\),
\(\therefore \overrightarrow{M N}=\overrightarrow{M D}+\overrightarrow{D A}+\overrightarrow{A N}=-\dfrac{1}{2} \overrightarrow{D D} \vec{D}_{1}-\overrightarrow{A D}+\dfrac{1}{3} \overrightarrow{A C}_{1}\).
\(=-\dfrac{1}{2} \overrightarrow{A A}_{1}-\overrightarrow{A D}+\dfrac{1}{3}\left(\overrightarrow{A A_{1}}+\overrightarrow{A D}+\overrightarrow{A B}\right)\)
\(=\dfrac{1}{3} \overrightarrow{A B}-\dfrac{2}{3} \overrightarrow{A D}-\dfrac{1}{6} \overrightarrow{A A_{1}}=\dfrac{1}{3} \vec{a}-\dfrac{2}{3} \vec{b}-\dfrac{1}{6} \vec{c}\). -
【答案】 \(\dfrac{1}{3}\overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{6} \overrightarrow{A D}\)
【解析】 三棱锥\(A-BCD\)中,\(P\)为\(△BCD\)内一点,如图所示:
延长\(PB\)至\(B_1\),使得\(PB_1=2PB\),延长\(PC\)至\(C_1\),
使得\(PC_1=3PC\),连接\(DB_1\),\(B_1 C_1\),\(C_1 D\),
因为\(S_{\triangle P B C}=1\), \(S_{\triangle P C D}=2\),\(S_{\triangle P B D}=3\),
所以 \(S_{\triangle P B_1 C_1}=S_{\triangle P C_1 D}=S_{\triangle P B_1 D}\),
所以\(P\)为\(△B_1 C_1 D\)的重心,所以 \(\overrightarrow{P D}+\overrightarrow{P B_1}+\overrightarrow{P C_1}=\overrightarrow{0}\),
即 \(\overrightarrow{P D}+2 \overrightarrow{P B}+3 \overrightarrow{P C}=\overrightarrow{0}\),
所以\((\overrightarrow{A D}-\overrightarrow{AP})+2(\overrightarrow{A B}-\overrightarrow{AP})+3(\overrightarrow{A C}-\overrightarrow{AP})=\overrightarrow{0}\),
所以\(\overrightarrow{AP}=\dfrac{1}{3}\overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{6} \overrightarrow{A D}\).

【题型二】空间向量共线共面问题
【典题1】 如图,在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(E\)在\(A_1 D_1\)上,且\(\overrightarrow{A_1 E}=2 \overrightarrow{E D_1}\),\(F\)在对角线\(A_1 C\)上,且\(\overrightarrow{A_1 F}=\dfrac{2}{3} \overrightarrow{F C}\),求证:\(E\),\(F\),\(B\)三点共线.

【解析】 设\(\overrightarrow{A B}=\overrightarrow{a}\),\(\overrightarrow{A D}=\overrightarrow{b}\),\(\overrightarrow{A A_1}=\vec{c}\)
\(\therefore \overrightarrow{E B}=\overrightarrow{E A_1}+\overrightarrow{A_1 A}+\overrightarrow{A B}=\dfrac{2}{3} \overrightarrow{D A}-\overrightarrow{A A_1}+\overrightarrow{A B}\)\(=\vec{a}-\vec{c}-\dfrac{2}{3} \vec{b}\),
\(\because \overrightarrow{A_1 E}=2 \overrightarrow{E D_1}\), \(\overrightarrow{A_1 F}=\dfrac{2}{3} \overrightarrow{F C}\), \(\therefore \overrightarrow{A_1 E}=\dfrac{2}{3} \overrightarrow{A_1 D_1}\),\(\overrightarrow{A_1 F}=\dfrac{2}{5} \overrightarrow{A_1 C}\)
\(\therefore \overrightarrow{A_1 E}=\dfrac{2}{3} \overrightarrow{A D}=\dfrac{2}{3} \vec{b}\),
\(\overrightarrow{A_1 F}=\dfrac{2}{5}\left(\overrightarrow{A C}-\overrightarrow{A A_1}\right)=\dfrac{2}{5}\left(\overrightarrow{A B}+\overrightarrow{A D}-\overrightarrow{A A_1}\right)\)\(=\dfrac{2}{5} \vec{a}+\dfrac{2}{5} \vec{b}-\dfrac{2}{5} \vec{c}\),
\(\therefore \overrightarrow{E F}=\overrightarrow{A_1 F}-\overrightarrow{A_1 E}=\dfrac{2}{5} \vec{a}-\dfrac{4}{15} \vec{b}-\dfrac{2}{5} \vec{c}=\dfrac{2}{5}\left(\vec{a}-\dfrac{2}{3} \vec{b}-\vec{c}\right)\),
又\(∵\)由(1)知 \(\overrightarrow{E B}=\vec{a}-\dfrac{2}{3} \vec{b}-\vec{c}\),
\(\therefore \overrightarrow{E F}=\dfrac{2}{5} \overrightarrow{E B}\),且有公共点\(E\),
所以\(E\),\(F\),\(B\)三点共线.
【典题2】 已知\(A\),\(B\),\(M\)三点不共线,对于平面\(ABM\)外的任意一点\(O\),判断在下列各条件下的点\(P\)与点\(A\),\(B\),\(M\)是否共面.
(1)\(\overrightarrow{OB}+\overrightarrow{OM}=3\overrightarrow{OP}-\overrightarrow{OA}\); \(\qquad \qquad\) (2)\(\overrightarrow{OP}=4\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OM}\).
【解析】 (1)\(∵A\),\(B\),\(M\)三点不共线,故\(A\),\(B\),\(M\)三点共面,
又\(∵\)对于平面\(ABM\)外的任意一点\(O\),
若\(\overrightarrow{OB}+\overrightarrow{OM}=3\overrightarrow{OP}-\overrightarrow{OA}\),
则 \(\overrightarrow{O P}=\dfrac{1}{3} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{3} \overrightarrow{O M}\),
\(\because \dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}=1\),故点\(P\)与\(A\),\(B\),\(M\)共面,
(2)\(∵A\),\(B\),\(M\)三点不共线,故\(A\),\(B\),\(M\)三点共面,
又\(∵\) 对于平面\(ABM\)外任意一点 ,
若\(\overrightarrow{OP}=4\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OM}\),则\(4-1-1=2≠1\),
故点\(P\)与\(A\),\(B\),\(M\)不共面.
【典题3】 如图所示,已知四边形\(ABCD\)是平行四边形,\(P\)点是四边形\(ABCD\)所在平面外一点,连接\(PA\)、\(PB\)、\(PC\)、\(PD\),设点\(E\),\(F\),\(G\),\(H\)分别为\(△PAB\)、\(△PBC\)、\(△PCD\)、\(△PDA\)的重心.试用向量法证明\(E\),\(F\),\(G\),\(H\)四点共面.

【解析】 分别延长\(PE\),\(PF\),\(PG\)、\(PH\),交对边于\(M\),\(N,\)\(Q\),\(R\)点,
因为\(E\),\(F\),\(G\),\(H\)分别是所在三角形的重心,
所以\(M\),\(N,\)\(Q\),\(R\)为所在边的中点,
顺次连接\(M\),\(N,\)\(Q\),\(R\)得到的四边形为平行四边形,
且有\(\overrightarrow{PE}=\dfrac{2}{3}\overrightarrow{PM}\),\(\overrightarrow{PF}=\dfrac{2}{3}\overrightarrow{PN}\), \(\overrightarrow{P G}=\dfrac{2}{3} \overrightarrow{P Q}\),\(\overrightarrow{PH}=\dfrac{2}{3}\overrightarrow{PR}\);如图所示,

\(∴\overrightarrow{MQ}=\overrightarrow{MN}+\overrightarrow{MR}=(\overrightarrow{PN}-\overrightarrow{PM} )+(\overrightarrow{PR}-\overrightarrow{PM} )\)
\(=\dfrac{3}{2}(\overrightarrow{PF}-\overrightarrow{PE})+\dfrac{3}{2}(\overrightarrow{PH}-\overrightarrow{PE})=\dfrac{3}{2}(\overrightarrow{EF}+\overrightarrow{EH})\);
又 \(Q \because \overrightarrow{M Q}=\overrightarrow{P Q}-\overrightarrow{P M}=\dfrac{3}{2} \overrightarrow{P G}-\dfrac{3}{2} \overrightarrow{P E}=\dfrac{3}{2} \overrightarrow{E G}\),
\(∴\dfrac{3}{2} \overrightarrow{EG}=\dfrac{3}{2}(\overrightarrow{EF}+\overrightarrow{EH})\),\(∴\overrightarrow{EG}=\overrightarrow{EF}+\overrightarrow{EH}\)
由共面向量定理知:\(E\),\(F\),\(G\),\(H\)四点共面.
巩固练习
1 (★) 已知向量\(\overrightarrow{a}\),\(\overrightarrow{b}\)且\(\overrightarrow{A B}=\overrightarrow{a}+2\overrightarrow{b}\),\(\overrightarrow{BC}=-5\overrightarrow{a}+6\overrightarrow{b}\),\(\overrightarrow{CD}=7\overrightarrow{a}-2\overrightarrow{b}\),则一定共线的三点为( )
A.\(A\),\(B\),\(D\) \(\qquad \qquad \qquad\) B.\(A\),\(B\),\(C\) \(\qquad \qquad \qquad\) C.\(B\),\(C\),\(D\) \(\qquad \qquad \qquad\) D.\(A\),\(C\),\(D\)
2(★) 在下列条件中,使\(M\)与\(A\),\(B\),\(C\)一定共面的是( )
A.\(\overrightarrow{O M}=\overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}\)
B.\(\overrightarrow{O M}=\dfrac{1}{5} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\)
C.\(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}\)
D.\(\overrightarrow{O M}+\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{0}\)
3(★) (多选题)在以下命题中,不正确的命题有( )
A.若\(\overrightarrow{a}\)与\(\overrightarrow{b}\)共线,\(\overrightarrow{b}\)与\(\overrightarrow{c}\)共线,则\(\overrightarrow{a}\)与\(\overrightarrow{c}\)共线
B.若\(\overrightarrow{a}//\overrightarrow{b}\),则存在唯一的实数\(λ\),使\(\overrightarrow{a}=λ\overrightarrow{b}\)
C.对空间任意一点\(O\)和不共线的三点\(A\),\(B\),\(C\),若\(\overrightarrow{OP}=2\overrightarrow{OA}+2\overrightarrow{OB}-3\overrightarrow{OC}\),则\(P\),\(A\),\(B\),\(C\)四点共面
D.若两个非零空间向量\(\overrightarrow{A B}\),\(\overrightarrow{CD}\)满足\(\overrightarrow{A B}+\overrightarrow{CD}=\overrightarrow{0}\),则\(\overrightarrow{A B}//\overrightarrow{CD}\)
4 (★★) 已知在正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(P\),\(M\)为空间任意两点,如果有 \(\overrightarrow{P M}=\overrightarrow{P B_1}+7 \overrightarrow{B A}+6 \overrightarrow{A A_1}-4 \overrightarrow{A_1 D_1}\),那么点\(M\)必在平面\(\underline{\quad \quad}\)内.
5 (★★) 在棱长为\(1\)的正方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(E\),\(F\),\(G\)分别在棱\(BB_1\),\(BC\),\(BA\)上,且满足 \(\overrightarrow{B E}=\dfrac{3}{4} \overrightarrow{B B_1}\), \(\overrightarrow{B F}=\dfrac{1}{2} \overrightarrow{B C}\), \(\overrightarrow{B G}=\dfrac{1}{2} \overrightarrow{B A}\),\(O\)是平面\(B_1 GF\),平面\(ACE\)与平面\(B_1 BDD_1\)的一个公共点,设 \(\overrightarrow{B O}=x \overrightarrow{B G}+y \overrightarrow{B F}+z \overrightarrow{B E}\),则\(x+y+z=\) \(\underline{\quad \quad}\) .
6 (★) 如图,在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\),\(N\)分别是\(C_1 D_1\),\(AB\)的中点,\(E\)在\(AA_1\)上且\(AE=2EA_1\),\(F\)在\(CC_1\)上且\(CF=\dfrac{1}{2} FC_1\),判断\(\overrightarrow{ME}\)与\(\overrightarrow{NF}\)是否共线?

7(★★) 已知\(\overrightarrow{e_1}\),\(\overrightarrow{e_2}\)为两个不共线的非零向量,且 \(\overrightarrow{A B}=\overrightarrow{e_1}+\overrightarrow{e_2}\),\(\overrightarrow{A C}=2\overrightarrow{e_1}+8\overrightarrow{e_2}\),\(\overrightarrow{A D}=3\overrightarrow{e_1}-3\overrightarrow{e_2}\),求证:\(A\),\(B\),\(C\),\(D\)四点共面.
8 (★★) 如图所示,在长方体\(ABCD-A_1 B_1 C_1 D_1\)中,\(M\)为\(DD_1\)的中点,\(N∈AC\),且\(AN:NC=2\),求证:\(A_1\),\(B\),\(N\),\(M\)四点共面.

9 (★★) 已知\(\overrightarrow{e_1}\),\(\overrightarrow{e_2}\),\(\overrightarrow{e_3}\)是不共面的向量,且\(\overrightarrow{OP}=2\overrightarrow{e_1}-\overrightarrow{e_2}+3\overrightarrow{e_3}\),\(\overrightarrow{OA}=\overrightarrow{e_1}+2\overrightarrow{e_2}-\overrightarrow{e_3}\),\(\overrightarrow{OB}=-3\overrightarrow{e_1}+\overrightarrow{e_2}+2\overrightarrow{e_3}\),\(\overrightarrow{OC}=\overrightarrow{e_1}+\overrightarrow{e_2}-\overrightarrow{e_3}\).
(1)判断\(P\),\(A\),\(B\),\(C\)四点是否共面;\(\qquad \qquad\) (2)能否\(\overrightarrow{OA}\),\(\overrightarrow{OB}\),\(\overrightarrow{OC}\)用表示\(\overrightarrow{OP}\)?并说明理由.
10(★★★) 已知\(O,A,B,C,D,F,F,G,H\)为空间\(9\)个点(如图),并且 \(\overrightarrow{O E}=k \overrightarrow{O A}\),\(\overrightarrow{O F}=k \overrightarrow{O B}\), \(\overrightarrow{O H}=k \overrightarrow{O D}\), \(\overrightarrow{A C}=\overrightarrow{A D}+m \overrightarrow{A B}\),\(\overrightarrow{E G}=\overrightarrow{E H}+m \overrightarrow{E F}\) .
求证:(1)\(A\),\(B\),\(C\),\(D\)四点共面;\(\qquad \qquad\) (2)\(\overrightarrow{A C}//\overrightarrow{EG}\);\(\qquad \qquad\)(3) \(\overrightarrow{O G}=k \overrightarrow{O C}\).

参考答案
-
【答案】 \(A\)
【解析】 因为\(\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}=-5\overrightarrow{a}+6\overrightarrow{b}+7\overrightarrow{a}-2\overrightarrow{b}=2\overrightarrow{a}+4\overrightarrow{b}=2\overrightarrow{A B}\),
所以\(\overrightarrow{A B}\)与\(\overrightarrow{BD}\)共线,即\(A\),\(B\),\(D\) 三点共线. -
【答案】 \(C\)
【解析】 在\(C\)中,由\(\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}\),得\(\overrightarrow{M A}=-\overrightarrow{M B}-\overrightarrow{M C}\),
则\(\overrightarrow{M A}, \overrightarrow{M B}, \overrightarrow{M C}\)为共面向量,即\(M、A、B、C\)四点共面;
对于\(A\),由\(\overrightarrow{O M}=\overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}\),得\(1-1-1=-1≠1\),不能得出\(M、A、B、C\)四点共面;
对于\(B\),由\(\overrightarrow{O M}=\dfrac{1}{5} \overrightarrow{O A}+\dfrac{1}{3} \overrightarrow{O B}+\dfrac{1}{2} \overrightarrow{O C}\),得\(\dfrac{1}{5}+\dfrac{1}{3}+\dfrac{1}{2} \neq 1\),所以\(M、A、B、C\)四点不共面;
对于\(D\),由\(\overrightarrow{O M}+\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{0}\),得\(\overrightarrow{O M}=-(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C})\),其系数和不为\(1\),
所以\(M、A、B、C\)四点不共面.
故选:\(C\). -
【答案】 \(AB\)
【解析】 当\(\overrightarrow{b}=\overrightarrow{0}\),满足\(\overrightarrow{a}\)与\(\overrightarrow{b}\)共线,\(\overrightarrow{b}\)与\(\overrightarrow{c}\)共线,
而\(\overrightarrow{a}\)与\(\overrightarrow{c}\)不一定共线,故\(A\)错误;
当\(\overrightarrow{a}\)与\(\overrightarrow{b}\)均为零向量时,能够保证\(\overrightarrow{a}//\overrightarrow{b}\),则存在无数多的实数\(λ\),
使得\(\overrightarrow{a}=λ\overrightarrow{b}\),故\(B\) 错误;
\(∵\overrightarrow{OP}=2\overrightarrow{OA}+2\overrightarrow{OB}-3\overrightarrow{OC}\),
即\(\overrightarrow{OP}-\overrightarrow{OA}=(\overrightarrow{OA}-\overrightarrow{OC})+2(\overrightarrow{OB}-\overrightarrow{OC})\),
\(∴\overrightarrow{AP}=\overrightarrow{CA}+2\overrightarrow{CB}\),
由平面向量基本定理可得\(P\),\(A\),\(B\),\(C\)四点共面,故\(C\)正确;
\(∵\)非零空间向量\(\overrightarrow{A B}\),\(\overrightarrow{CD}\)满足\(\overrightarrow{A B}+\overrightarrow{CD}=\overrightarrow{0}\),
\(∴\overrightarrow{A B}=-\overrightarrow{CD}\),\(∴\overrightarrow{A B}//\overrightarrow{CD}\),故\(D\)正确.
故选:\(AB\). -
【答案】 \(BA_1 D_1\)
【解析】 因为 \(\overrightarrow{P M}=\overrightarrow{P B_1}+7 \overrightarrow{B A}+6 \overrightarrow{A A_1}-4 \overrightarrow{A_1 D_1}=\overrightarrow{P B_1}+\overrightarrow{B A}+6 \overrightarrow{B A_1}-4 \overrightarrow{A_1 D_1}\)
\(=\overrightarrow{P B_1}+\overrightarrow{B_1 A_1}+6 \overrightarrow{B A_1}-4 \overrightarrow{A_1 D_1}=\overrightarrow{P A_1}+6\left(\overrightarrow{P A_1}-\overrightarrow{P B}\right)-4\left(\overrightarrow{P D_1}-\overrightarrow{P A_1}\right)\)
\(=11 \overrightarrow{P A_1}-6 \overrightarrow{P B}-4 \overrightarrow{P D_1}\),
所以\(M\),\(B\),\(A_1\),\(D_1\)四点共面,即点\(M\)必在平面\(BA_1 D_1\)内. -
【答案】 \(\dfrac{6}{5}\)
【解析】 如图所示,
正方体\(ABCD-A_1 B_1 C_1 D_1\)中, \(\overrightarrow{B E}=\dfrac{3}{4} \overrightarrow{B B_1}\), \(\overrightarrow{B F}=\dfrac{1}{2} \overrightarrow{B C}\), \(\overrightarrow{B G}=\dfrac{1}{2} \overrightarrow{B A}\),
\(\overrightarrow{B O}=x \overrightarrow{B G}+y \overrightarrow{B F}+z \overrightarrow{B E}=\dfrac{1}{2} x \overrightarrow{B A}+\dfrac{1}{2} y \overrightarrow{B C}+z \overrightarrow{B E}\)\(=x \overrightarrow{B G}+y \overrightarrow{B F}+\dfrac{3}{4} z \overrightarrow{B B_1}\),
\(∵O\),\(A\),\(C\),\(E\)四点共面,\(O\),\(D\),\(E\),\(B_1\)四点共面,
\(\therefore\left\{\begin{array}{l} \dfrac{1}{2} x+\dfrac{1}{2} y+z=1 \\ x+y+\dfrac{3}{4} z=1 \end{array}\right.\),解得\(x+y=\dfrac{2}{5}\),\(z=\dfrac{4}{5}\);
\(∴x+y+z=\dfrac{6}{5}\). -
【答案】 共线
【解析】 由已知可得: \(\overrightarrow{M E}=\overrightarrow{M D_1}+\overrightarrow{D_1 A_1}+\overrightarrow{A_1 E}\)
\(=\dfrac{1}{2} \overrightarrow{B A}+\overrightarrow{C B}+\dfrac{1}{3} \overrightarrow{A_1 A}=-\overrightarrow{N B}+\overrightarrow{C B}+\dfrac{1}{3} \overrightarrow{C_1 C}\)\(=\overrightarrow{C N}+\overrightarrow{F C}=\overrightarrow{F N}=-\overrightarrow{N F}\).
所以\(\overrightarrow{ME}=-\overrightarrow{NF}\),故\(\overrightarrow{ME}\)与\(\overrightarrow{NF}\)共线. -
【证明】 设\(\overrightarrow{A C}=x\overrightarrow{A B}+y\overrightarrow{A D}\),则\(2\overrightarrow{e_1}+8\overrightarrow{e_2}=x(\overrightarrow{e_1}+\overrightarrow{e_2} )+y(3\overrightarrow{e_1}-3\overrightarrow{e_2} )\),
\(∴(2-x-3y)\overrightarrow{e_1}+(8-x+3y)\overrightarrow{e_2}=\overrightarrow{0}\),
又\(\overrightarrow{e_1}\),\(\overrightarrow{e_2}\)为两个不共线的非零向量,
\(\therefore\left\{\begin{array}{l} 2-x-3 y=0 \\ 8-x+3 y=0 \end{array}\right.\), \(\therefore\left\{\begin{array}{l} x=5 \\ y=-1 \end{array}\right.\),
\(∴\overrightarrow{A C}=5\overrightarrow{A B}-\overrightarrow{A D}\),
\(∴A\),\(B\),\(C\),\(D\)四点共面,
故原命题得证. -
【证明】 设 \(\overrightarrow{A A_1}=\overrightarrow{a}\),\(\overrightarrow{A B}=\overrightarrow{b}\),\(\overrightarrow{A D}=\overrightarrow{c}\),则\((A_1 B) ⃗=\overrightarrow{b}-\overrightarrow{a}\),
\(∵M\)为\(DD_1\)的中点,\(∴\overrightarrow{A_1 M} =\overrightarrow{c}-\dfrac{1}{2} \overrightarrow{a}\),
又\(∵AN:NC=2\),\(\therefore \overrightarrow{A N}=\dfrac{2}{3} \overrightarrow{A C}=\dfrac{2}{3}(\vec{b}+\vec{c})\),
\(\therefore \overrightarrow{A_1 N}=\overrightarrow{A N}-\overrightarrow{A A_1}=\dfrac{2}{3}(\vec{b}+\vec{c})-\vec{a}\)\(=\dfrac{2}{3}(\vec{b}-\vec{a})+\dfrac{2}{3}\left(\vec{c}-\dfrac{1}{2} \vec{a}\right)=\dfrac{2}{3} \overrightarrow{A_1 B}+\dfrac{2}{3} \overrightarrow{A_1 M}\),
\(\therefore \overrightarrow{A_1 N}\), \(\overrightarrow{A_1 B}\), \(\overrightarrow{A_1 M}\)为共面向量,
又三向量有相同的起点\(A_1\),\(∴A_1\),\(B\),\(N\),\(M\)四点共面. -
【答案】 (1) 不共面 (2) \(\overrightarrow{OP}=17\overrightarrow{OA}-5\overrightarrow{OB}-30\overrightarrow{OC}\)
【解析】 (1)假设\(P\),\(A\),\(B\),\(C\)四点共面,
则存在实数\(x\),\(y\),\(z\),使得\(\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}\),且\(x+y+z=1\),
即 \(2 \vec{e}_1-\vec{e}_2+3 \vec{e}_3=x\left(\overrightarrow{e_1}+2 \vec{e}_2-\vec{e}_3\right)+y\left(-3 \vec{e}_1+\overrightarrow{e_2}+2 \vec{e}_3\right)+z\left(\overrightarrow{e_1}+\overrightarrow{e_2}-\overrightarrow{e_3}\right)\)
比较对应的系数,得到 \(\left\{\begin{array}{l} x-3 y+z=2 \\ 2 x+y+z=-1 \\ -x+2 y-z=3 \end{array}\right.\),解得 \(\left\{\begin{array}{l} x=17 \\ y=-5 \\ z=-30 \end{array}\right.\),
这与\(x+y+z=1\)矛盾,
故\(P\),\(A\),\(B\),\(C\)四点不共面;
(2)若\(\overrightarrow{OA}\),\(\overrightarrow{OB}\),\(\overrightarrow{OC}\)共面,则存在\(m\),\(n\),使得\(\overrightarrow{OA}=m\overrightarrow{OB}+n\overrightarrow{OC}\),
同(1)可证,\(\overrightarrow{OA}\),\(\overrightarrow{OB}\),\(\overrightarrow{OC}\)不共面,即\(\overrightarrow{OP}\)是向量\(\overrightarrow{OA}\),\(\overrightarrow{OB}\)与\(\overrightarrow{OC}\)的线性组合,
令\(\overrightarrow{OA}=\overrightarrow{a}\),\(\overrightarrow{OB}=\overrightarrow{b}\),\(\overrightarrow{OC}=\overrightarrow{c}\),
由 \(\left\{\begin{array}{l} \overrightarrow{e_1}+2 \overrightarrow{e_2}-\overrightarrow{e_3}=\vec{a} \\ -3 \overrightarrow{e_1}+\overrightarrow{e_2}+2 \overrightarrow{e_3}=\vec{b} \\ \overrightarrow{e_1}+\overrightarrow{e_2}-\overrightarrow{e_3}=\vec{c} \end{array}\right.\),得 \(\left\{\begin{array}{l} \overrightarrow{e_1}=3 \vec{a}-\vec{b}-5 \vec{c} \\ \overrightarrow{e_2}=\vec{a}-\vec{c} \\ \overrightarrow{e_3}=4 \vec{a}-\vec{b}-7 \vec{c} \end{array}\right.\),
所以 \(\overrightarrow{O P}=2 \vec{e}_1-\vec{e}_2+3 \vec{e}_3=2(3 \vec{a}-\vec{b}-5 \vec{c})-(\vec{a}-\vec{c})+3(4 \vec{a}-\vec{b}-7 \vec{c})\)
\(=17 \vec{a}-5 \vec{b}-30 \vec{c}=17 \overrightarrow{O A}-5 \overrightarrow{O B}-30 \overrightarrow{O C}\). -
【证明】 (1)\(∵\overrightarrow{A C}=\overrightarrow{A D}+m\overrightarrow{A B}\),
\(∴\)由共面向量基本定理得\(\overrightarrow{A C}\),\(\overrightarrow{A D}\),\(\overrightarrow{A B}\)是共面向量,
\(∵\overrightarrow{A C}\),\(\overrightarrow{A D}\),\(\overrightarrow{A B}\)有公共点\(A\),
\(∴A\),\(B\),\(C\),\(D\)四点共面.
(2) \(\because \overrightarrow{E G}=\overrightarrow{E H}+m \overrightarrow{E F}=\overrightarrow{O H}-\overrightarrow{O E}+m(\overrightarrow{O F}-\overrightarrow{O E})\) \(=k(\overrightarrow{A D}-\overrightarrow{O A})+k m(\overrightarrow{O B}-\overrightarrow{O A})\)
\(=k \overrightarrow{A D}+k m \overrightarrow{A B}=k(\overrightarrow{A D}+m \overrightarrow{A B})=k \overrightarrow{A C}\),
\(∴\overrightarrow{A C}//\overrightarrow{EG}\).
(3)由(1)知 \(\overrightarrow{O G}=\overrightarrow{E G}-\overrightarrow{E O}=k \overrightarrow{A C}-k \overrightarrow{A O}=k(\overrightarrow{A C}-\overrightarrow{A O})=k \overrightarrow{O C}\),
\(\therefore \overrightarrow{O G}=k \overrightarrow{O C}\).