§ 1 卡尔曼滤波KF
概述
自己总结:基础的卡尔曼滤波完成了这样的一件事:在一系列线性的前提条件下,在状态转移模型具有正态分布、测量模型具有正态分布的情况下,给出了一个满足正态分布的估计。
前提条件
满足以下条件,则卡尔曼滤波给出的后验状态估计满足正态分布:
-
下次状态是上状态的线性变换再加上一个满足正态分布的随机误差,这也称为运动模型。下式中的\(\varepsilon_t\)是满足均值为0的正态分布的噪声。
\[x_t=A_tx_{t-1}+B_tu_t+\varepsilon_t\\ \Leftrightarrow p(x_t\mid u_t,x_{t-1})=\det(2\pi R_t)^{-\frac{1}{2}}\\ \exp\left[-\frac{1}{2}(x_t-A_tx_{t-1}-B_tu_t)^TR_t^{-1}(x_t-A_tx_{t-1}-B_tu_t) \right] \] -
测量结果是状态的线性变换加上一个满足正态分布的随机误差。同上,\(\delta_t\)也是一个满足均值为0的正态分布的噪声。
\[z_t=C_tx_t+\delta_t\\ \Leftrightarrow p(z_t\mid x_{t})=\det(2\pi Q_t)^{-\frac{1}{2}}\exp\left[-\frac{1}{2}(z_t-C_tx_{t})^TQ_t^{-1}(z_t-C_tx_{t}) \right] \] -
初始的估计满足正态分布。
\[bel(x_0)=\det(2\pi \Sigma_0)^{-\frac{1}{2}}\exp\left[-\frac{1}{2}(x_0-\mu_0)^T\Sigma_0^{-1}(x_0-\mu_0) \right] \]
算法内容
满足以上条件时,卡尔曼滤波按照以下步骤给出满足正态分布的新估计的均值与方差。
输入:\(\mu_{t-1},\Sigma_{t-1},u_t,z_t\)
输出:\(\mu_t,\Sigma_t\)
-
根据控制量与上一次的状态做出估计
\[\begin{aligned} &\bar{\mu}_t=A_t \mu_{t-1}+B_t u_t \\ &\bar{\Sigma}_t=A_t \Sigma_{t-1} A_t^T+R_t \\ \end{aligned} \] -
使用测量结果更新估计
\[\begin{aligned} &K_t=\bar{\Sigma}_t C_t^T\left(C_t \bar{\Sigma}_t C_t^T+Q_t\right)^{-1} \\ &\mu_t=\bar{\mu}_t+K_t\left(z_t-C_t \bar{\mu}_t\right) \\ &\Sigma_t=\left(I-K_t C_t\right) \bar{\Sigma}_t \end{aligned} \]
推导过程一览
-
首先明确一下要推导的是什么:采用下列估计方法
\[\begin{aligned} &bel(\bar x)=\int_{-\infty}^{\infty}p(x_t\mid x_{t-1},u_t)p(x_{t-1})\mathrm dx_{t-1}\\ &bel(x_t)=\eta p(z_t\mid x_t)bel(\bar x) \end{aligned} \]则可以满足\(bel(\bar x_t)=\mathcal N(\bar\mu_t,\bar\Sigma_t),bel(x_t)=\mathcal N(\mu_t,\Sigma_t)\)。
这里的等号右边一个像全概率定理,一个像贝叶斯准则,但仔细一看又并不是这俩公式。
从这里便可以感受到估计\(bel\)(belief)与概率\(p\)(probability)的不同。个人感觉估计是带有一定主观因素的,而概率则是建立在概率论的数学基础上的。
-
证明过程也即是将等号右端的各项带入并化简为标准正态分布的形式,最终得到算法内容中描述的\(\mu_t,\Sigma_t\)的解析表达式。过程中涉及不少关于矩阵微分、求逆的操作。
b站DR_CAN的视频中介绍了另一种得到卡尔曼增益\(K_t\)的推导思路。该思路从另一个角度切入,寻求使用不太准的模型预测结果\(\bar\mu_t\)与测量结果反推的\(C_t^{-1}z_t\)线性组合来得到更准确的估计,于是就有了下式:
\[\begin{aligned} \mu_t&=\alpha C_t^{-1}z_t+(1-\alpha)\bar\mu\\ &=\bar\mu+\alpha(C_t^{-1}z_t-\bar\mu)\\ &=\bar\mu+\alpha C_t^{-1}(z_t-C_t\bar\mu) \end{aligned} \]一个准确的估计的方差应该尽可能小,选择合适的\(\alpha\)使得\(\mu_t\)的方差达到最小,恰好就可以发现\(\alpha C_t^{-1=K_t\)。
§ 2 扩展卡尔曼滤波EKF
概述
在卡尔曼滤波基础之上,扩展卡尔曼滤波尝试放宽前提条件中的1和2,也它在即尝试处理状态转移模型和测量模型不是线性的情况。扩展卡尔曼滤波面对非线性时所采取的的方法是比较简单的:在上一次估计的均值处进行一阶近似,然后用所得的线性模型代替非线性模型,剩余内容就和卡尔曼滤波相同了。
算法内容
假设现在的运动模型和测量模型为
\[x_t=g(x_{t-1},u_t)+\varepsilon_t\\ z_t=h(x_t)+\delta_t \]定义\(G\)和\(H\)为
\[G_t=\frac{\partial g(x_{t-1},u_t)}{\partial x_{t-1}}\\ H_t=\frac{\partial h(x_{t})}{\partial x_{t-1}} \]则扩展卡尔曼滤波表示为
-
根据控制量与上一次的状态做出估计
\[\begin{aligned} &\bar{\mu}_t=g(x_{t-1},u_t)\\ &\bar{\Sigma}_t=G_t \Sigma_{t-1} G_t^T+R_t \\ \end{aligned} \] -
使用测量结果更新估计
\[\begin{aligned} &K_t=\bar{\Sigma}_t H_t^T\left(H_t \bar{\Sigma}_t H_t^T+Q_t\right)^{-1} \\ &\mu_t=\bar{\mu}_t+K_t\left[z_t-h(\bar\mu_t)\right] \\ &\Sigma_t=\left(I-K_t H_t\right) \bar{\Sigma}_t \end{aligned} \]
影响近似好坏的因素
-
上一次估计的不确定性,不确定性越小,近似越准。
-
模型在上一次估计均值附近的线性程度,越接近线性,近似越准。
下边这两张图就分别说明了不确定性和线性程度对估计精度的影响,其中每一个子图的左上角的图中,虚线是扩展卡尔曼滤波的结果,未涂成灰色的实线是蒙特卡罗法的结果。
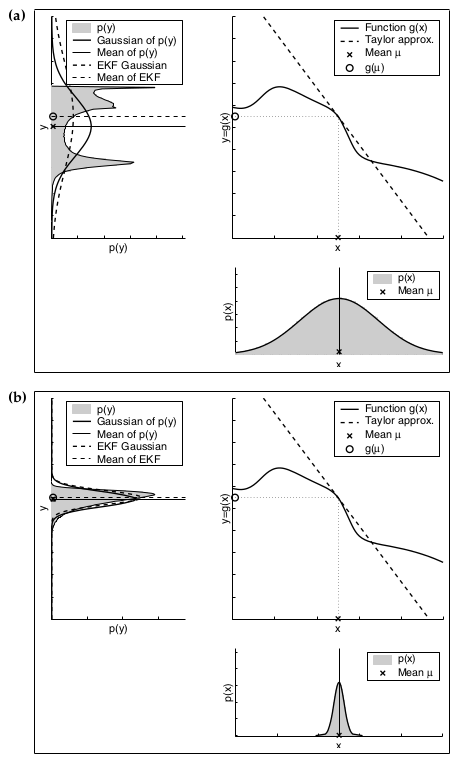
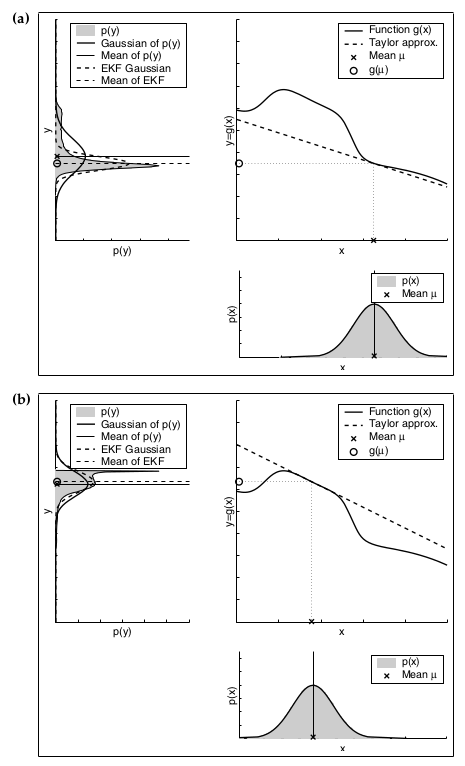
§ 3 无迹卡尔曼滤波UKF
前边两个卡尔曼中的先验估计的方差\(\bar\Sigma_t\)和测量模型的方差\(C_t\bar\Sigma_tC_t^T\)(KF)/\(H_t\bar\Sigma_tH_t^T\)(EKF)都是基于上一次的估计与状态转移模型计算的,而无迹卡尔曼滤波的方差则使用上一次的估计结合若干转移后的采样点直接计算。
书上给出了一种固定的取点方式,但对其合理性并未做太多说明。另外书中还有提到在不少的应用场景中UKF和EKF表现差不多,不过UKF在计算雅可比矩阵困难时会更有优势。
§ 4 信息滤波IF
各种KF中均使用均值和方差来描述正态分布,信息滤波则相当于是换了一组描述正态分布的参数的KF,其使用的信息矩阵\(\Omega\)与信息向量\(\xi\)定义如下:
\[\Omega=\Sigma^{-1}\\ \xi=\Sigma^{-1}\mu \]书上有提到\(IF\)相对\(KF\)的一些优缺点,暂时太理解。
标签:概率,bar,卡尔曼滤波,机器人,mu,第三章,aligned,Sigma,正态分布 From: https://www.cnblogs.com/harold-lu/p/16704440.html