概率论与数理统计公式自测
1.概率论基本概念
基本运算:
\[P(A - B) = \qquad \qquad \qquad \]\[P(A \cup B) = \qquad \qquad \qquad \]容斥原理二维、三维情况:
\[P(A \cup B) = \qquad \qquad \qquad \]\[P(A \cup B \cup C) = \qquad \qquad \qquad \]条件概率:
\[P(A | B) = \qquad \qquad \qquad \]乘法公式:
\[P(AB) = \qquad \qquad \qquad \]\[P(ABC) = \qquad \qquad \qquad \]全概率公式:
\[P(A) = \sum _{j = 1} ^ {n} P(AB_j) = \qquad \qquad \qquad \ \qquad \]贝叶斯公式:
\[P(B_i | A) = \frac {P(AB_i)} {P(A)} = \qquad \qquad \qquad \qquad \]2.一维随机变量及其分布
泊松分布 \(X \sim P( \lambda)\):
\[P(X = k) = \qquad \qquad \qquad \]均匀分布 \(X \sim U(a, b)\):
\[f(x) = \left\{\begin{align*}& \\& &\qquad \qquad \qquad \end{align*}\right. \]\[F(x) = \left\{\begin{align*}& \\ \\ \\ & & \qquad \qquad \qquad\end{align*}\right. \]指数分布 \(X \sim E( \lambda)\):
\[f(x) = \left\{\begin{align*}& \\& & \qquad \qquad \qquad\end{align*}\right. \]\[F(x) = \left\{\begin{align*}& \\ \\& & \qquad \qquad \qquad\end{align*}\right. \]正态分布 \(X\sim N(\mu,\sigma^2)\):
\[f(x) = \qquad \qquad \qquad \]\[\int_{-\infty}^{\infty} e^{-x^2} dx = \qquad \qquad \qquad \]3.二维随机变量及其分布
连续型的边缘概率密度:
\[f_X(x) = \qquad \qquad \qquad \]\[f_Y(y) = \qquad \qquad \qquad \]连续型的条件概率密度:
已知\(f(x,y)\),若 \(\forall y, f_Y(y) > 0\),则:
\[f_{X | Y}(x | y) = \qquad \qquad \]\(Z = X + Y\) 的分布:
\[f_Z(z) = \qquad \qquad \qquad \]\(Z = X \cdot Y\) 的分布:
\[f_Z(z) = \qquad \qquad \qquad \]\(Z = \frac {Y}{X}\)的分布:
\[f_Z(z) = \qquad \qquad \qquad \]极值分布:
\[F_{max}(z) = \qquad \qquad \qquad \]\[F_{min}(z) = \qquad \qquad \qquad \]4.随机变量的数字特征
期望:
\[E(C) = \qquad \qquad \qquad \]\[E(aX + bY) = \qquad \qquad \qquad \qquad \]若\(X,Y\)相互独立:
\[E(XY) = \qquad \qquad \qquad \]方差:
\[D(X) = \qquad \qquad \qquad\\ = \qquad \quad \]\[D(C) = \qquad \qquad \qquad \]\[D(aX + b) = \qquad \qquad \qquad \qquad \]\[D(X \pm Y) = \qquad \qquad \qquad \qquad \]协方差:
\[Cov(X, Y) = \qquad \qquad \qquad\\ = \quad \]\[Cov(X, X) = \qquad \qquad \qquad \]\[Cov(aX + b, cX + d) = \qquad \qquad \qquad \qquad \]\[Cov(X_1 \pm X_2, Y) = \qquad \qquad \qquad \qquad \]\[Cov(aX + bY, Z) = \qquad \qquad \qquad \qquad \]相关系数:
\[\rho_{XY} = \qquad \qquad\qquad \qquad \]难背的分布及其期望和方差:
\[\begin{array}{|c|l|l|l|l|} \hline {分布名称}&{参数}&{期望}&{方差}\\ \hline {泊松分布}&{}&{}&{}\\ \hline {几何分布}&{}&{}&{}\\ \hline {指数分布}&{}&{}&{}\\ \hline \end{array} \]5.大数定律和中心极限定理
切比雪夫不等式:
\[P\{|X-E(X)|\geq\varepsilon\}\leq \qquad \qquad \qquad \qquad \]6.数理统计
样本均值:
样本方差:
样本标准差:
样本 \(k\) 阶原点矩:
样本 \(k\) 阶中心矩:
八大分布:
单正态总体:
(1)提示:和正态有关的两个
\[{} \](2)提示:和卡方有关的第一个
\[{} \](3)提示:和卡方有关的第二个
\[{} \](4)提示:和t有关的
\[{} \]双正态总体:
(5)提示:和正态有关的
\[{} \](6)提示:和t有关的
\[{} \](7)提示:和F有关的第一个
\[{} \](8)提示:和F有关的第二个
\[{} \]7.参数估计
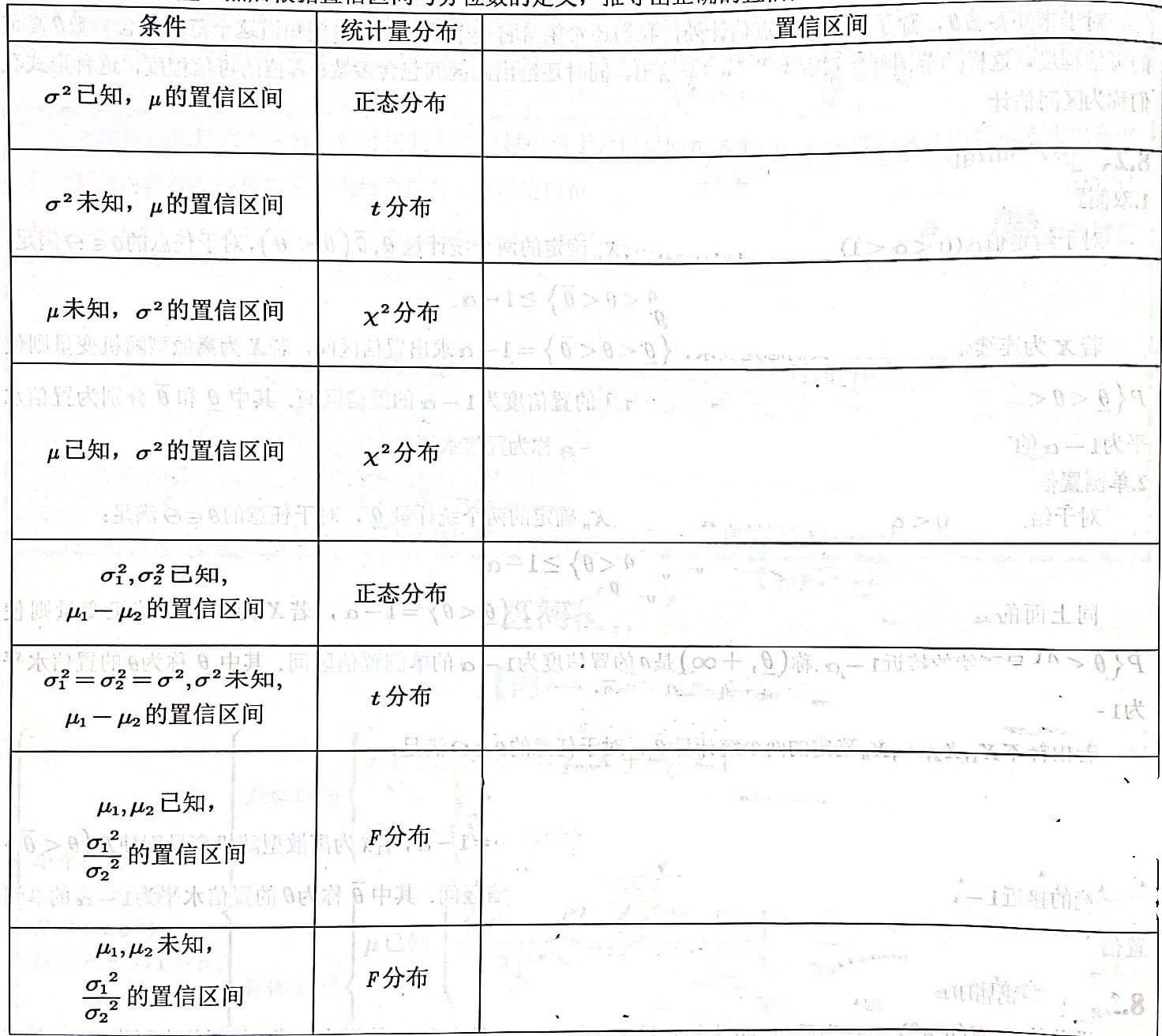
置信区间:
8.假设检验
咕咕咕......
标签:end,Cov,公式,align,自测,hline,分布,qquad,概率论 From: https://www.cnblogs.com/BeyondLimits/p/17154114.html