Simpson - 辛普森法 学习笔记
目录内容包括但不限于:自适应Simpson积分,拟合,广义积分(反常积分)及其收敛性的证明。
Tips:不保证正确性,不保证没锅,部分定理可能只是口糊的证明,也可能不会进行严谨证明。
更好的阅读体验戳此进入
目的
当我们求解定积分,或者说求曲边梯形面积的时候,可以通过把区间分为几个小区间然后再将小区间的积分求解求和,此时则需要 Simpson公式 了。
更具体地,我们会把定积分分成一些区间,然后对于每个区间用二次函数拟合,分别求解,最后求和。
拟合
这个东西简而言之呢,就是把平面上的一系列点用一条光滑曲线连结起来。
然后这里我们一般都考虑用一个高次多项式来表示这些点。显然如果用低次多项式拟合多个点,显然一定是无法准确连结所有点的,而如果强行用很高次的多项式去尽量连结所有的点,这种情况下大概会变成如下的形式:(图片来自知乎)
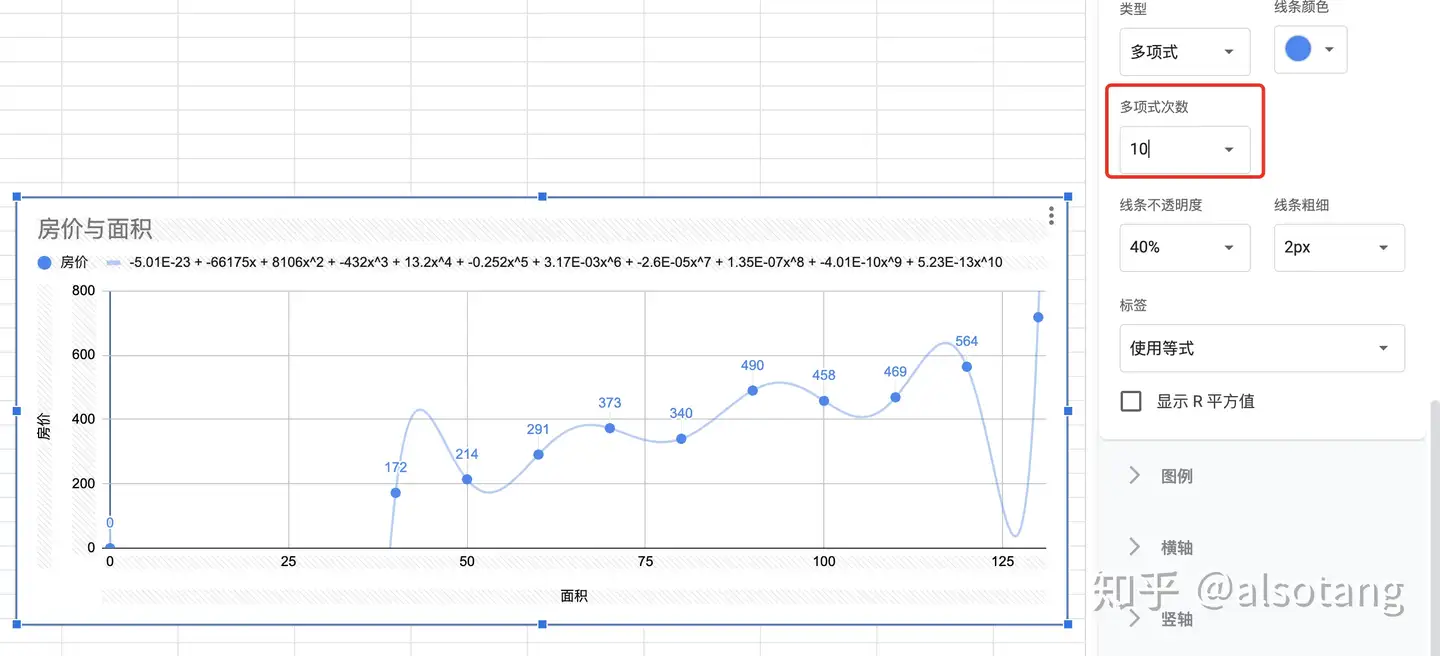
对于这种我们一般称其为过拟合。其坏处即为复杂度更大,预测性更小,以及很小的数据扰动会使公式剧烈变化。
参考自 拟合与过度拟合。
广义积分(反常积分)
定义
首先一般的定积分都是确定上下界的,否则我们也无法求出其对应的曲边梯形面积。然而对于收敛的积分我们也是可以计算的,例如当 $ x \to +\infty $ 时有 $ f(x) \to 0 $ 那么此时后面的面积也就认为可以忽略了,所以一般这种我们就称其为广义积分,或者叫反常积分。
然后这东西一般有两种,一种就是上述的边界为无穷的,称为无穷限广义积分。另一种是其含有瑕点(大概就是取不到的点?),称其为瑕积分。
(似乎瑕积分要求必须最多仅有一个瑕点?如果有多个瑕点需要分区间计算。
收敛性判断
首先这个东西如果我们 //TODO
写在前面
首先众所周知辛普森积分法一般选择二次函数进行拟合,原因是综合考量了时间和精确度。
如果用一次函数拟合,也就是梯形法积分,这样的精度过差。如果采用更高次函数,那么时间耗费过大。
对于一个 $ k $ 次函数,如果每次求取值需要 $ O(u) $,经过分析最后的复杂度大概是 $ O(k^2 + ku) $,如果使用过高次的函数,这个东西的复杂度就会变得不可接受。并且参考上面说的过拟合,如果多项式次数过高,预测性也会变小,数据扰动的副作用也更大。
参考自 为什么在用辛普森做定积分的时候用二次函数拟合目标函数?。
Simpson公式
首先我们需要知道牛顿-莱布尼茨公式,即:
\[\int_a^b f(x) dx = F(b) - F(a) = F(x) \vert_a^b \]其中 $ F'(x) = f(x) $。
则令原函数为 $ f(x) $,拟合后的二次函数为 $ g(x) = Ax^2 + Bx + C $,则令 $ G'(x) = g(x) $,有 $ G(x) = \dfrac{A}{3}x^3 + \dfrac{B}{2}x^2 + Cx $,则:
\[\begin{aligned} \int_a^b f(x)\mathrm{d}x &\approx \int_a^b Ax^2 + Bx + C \\ &= \dfrac{A}{3}(b^3 - a^3) + \dfrac{B}{2}(b^2 - a^2) + C(b - a) \\ &= \dfrac{A}{3}(b - a)(b^2 + ab + a^2) + \dfrac{B}{2}(b + a)(b - a) + C(b - a) \\ &= \dfrac{(b - a)}{6}(2A(b^2 + ab + a^2) + 3B(b + a) + 6C) \\ &= \dfrac{(b - a)}{6}(2Ab^2 + 2Aab + 2Aa^2 + 3Bb + 3Ba + 6C) \\ &= \dfrac{(b - a)}{6}(Aa^2 + Ba + C + Ab^2 + Bb + C + Ab^2 + 2Aab + Aa^2 + 2Bb + 2Ba + 4C) \\ &= \dfrac{(b - a)}{6}(Aa^2 + Ba + C + Ab^2 + Bb + C + A(a + b)^2 + 2B(a + b) + 4C) \\ &= \dfrac{(b - a)}{6}(Aa^2 + Ba + C + Ab^2 + Bb + C + 4A(\dfrac{a + b}{2})^2 + 4B(\dfrac{a + b}{2}) + 4C) \\ &= \dfrac{(b - a)}{6}(f(a) + f(b) + 4f(\dfrac{a + b}{2})) \end{aligned} \]于是我们就得到了 Simpson公式 的最终版本:
\[\int_a^b f(x)\mathrm{d}x = \dfrac{(b - a)(f(a) + f(b) + 4f(\dfrac{a + b}{2}))}{6} \]即:
double Simpson(double a, double b){
return (b - a) * (f(a) + f(b) + 4 * f((a + b) / 2.0)) / 6.0;
}
自适应积分
显然对于一个复杂的函数,我们无法用一个二次函数直接拟合它。所以我们可以考虑进行二分递归求解,直到误差足够小的时候再回溯求和。
具体地,对于一个区间 $ [l, r] $,我们可以对其用辛普森公式拟合,然后再对 $ [l, mid] $ 和 $ [mid, r] $ 分别求解,然后判断是否 $ \lvert S_{[l, mid]} + S_{[mid, r]} - S_{[l, r]} \vert \le eps $,如果是那么直接回溯,否则继续递归下去。
然后这里还有点提升精度的方法,就是判断时写成 $ \lvert S_{[l, mid]} + S_{[mid, r]} - S_{[l, r]} \vert \le eps \times 15 $,精度符合要求之后回溯的值为 $ S_{[l, mid]} + S_{[mid, r]} + \dfrac{S_{[l, mid]} + S_{[mid, r]} - S_{[l, r]}}{15} $。这个东西具体是为什么我也证不出来,能想到的大概就是因为 $ mid $ 处的值被重复计算了需要减掉。然后具体的证明能找到线索的就是《数值分析(原书第2版)》第 240 页左右,感兴趣可以看看,大致就是这么写可以提升一部分精度。
然后还有一个常用的写法就是每次递归都进行 $ eps \leftarrow \dfrac{eps}{2} $,这个比较好理解,可以考虑如果我们要保证在当前的误差不大于 $ eps $,那么两个左右区间的误差就都要在 $ \dfrac{eps}{2} $ 之内,这样的话最坏情况下两者误差加在一起也在可控范围内。总之就是这么写比较合适,可以提升精度。

例题#1
题面
计算积分:
\[\int_L^R \dfrac{cx + d}{ax + b}\mathrm{d}x \]Solution
标准模板题,自适应辛普森积分做一下即可。当然直接解积分也可以做。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template < typename T = int >
inline T read(void);
double a, b, c, d, L, R;
double f(double x){
return (c * x + d) / (a * x + b);
}
double Simpson(double a, double b){
return (b - a) * (f(a) + f(b) + 4 * f((a + b) / 2.0)) / 6.0;
}
double Adaptive(double l, double r, double cur, double eps = 1e-6){
double mid = (l + r) / 2.0;
double lval = Simpson(l, mid), rval = Simpson(mid, r);
if(fabs(lval + rval - cur) <= eps * 15.0)return lval + rval + (lval + rval - cur) / 15.0;
return Adaptive(l, mid, lval, eps / 2.0) + Adaptive(mid, r, rval, eps / 2.0);
}
int main(){
scanf("%lf%lf%lf%lf%lf%lf", &a, &b, &c, &d, &L, &R);
printf("%.6lf\n", Adaptive(L, R, Simpson(L, R)));
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
例题 #2
题面
求解积分:
\[\int_0^\infty x^{\frac{a}{x} - x}\mathrm{d}x \]$ eps = 10^{-5} $,若积分发散输出 orz。
Solution
首先放结论,若 $ a \lt 0 $ 那么函数发散,反之收敛,收敛的时候用刚才说的自适应辛普森跑一下就行。
然后对于上下界,首先 $ 0 $ 是不可以的,因为此时积分无意义,所以我们下界需要设为 $ eps $,而上界显然不可能是 $ \infty $,考虑如何设置,这里也有个结论,对于题里的函数,可以证明即使当 $ a = 50 $ 取到题目最大值,函数在 $ x = 20 $ 的时候就已经趋近于 $ 0 $ 了,所以整体范围设为 $ [eps, 20] $ 即可,然后这个东西如果朴素地写成 $ eps = 10^{-5} $ 会被卡精度,所以考虑将 $ eps = 10^{-7} $ 就可以通过了。对于刚才结论的具体证明可以参考下文。
然后考虑证明:TODO
例题 #3 难度天花板 - 龙与地下城
题面
给定一个 $ m $ 面的骰子,等概率产出 $ 0, 1, 2, \cdots, m - 1 $,投 $ n $ 次,求投出来的数之和在区间 $ [A, B] $ 的概率。
Solution
首先介绍一点前置知识:
正态分布:图形不再赘述,唯一需要注意的就是随机变量 $ X $ 的正态分布只需要它的期望 $ \mu $ 和方差 $ \sigma^2 $ 即可描述,记作 $ N(\mu, \sigma^2) $,不难发现这恰好对应着题干。
概率密度函数:依然考虑一个随机变量 $ X $,若其为离散的那么显然可以简单的求出任意点的概率。但若其为连续型的,那么一个点的概率在极限意义下为 $ 0 $,然然而查询一段区间的时候显然不为 $ 0 $,所以我们便引入了概率密度函数来描述这个概率,对于随机变量 $ X $ 的概率密度函数 $ f(x) $,需要满足 $ f(x) $ 在区间内的积分等于 $ X $ 落在该区间的概率。
然后有个结论:正态分布的概率密度函数为:
\[f(x) = \dfrac{1}{\sqrt{2 \pi \sigma^2}}e^{-\tfrac{(x - \mu)^2}{2\sigma^2}} \]关于这个东西的证明。。。完全不是人看的,似乎只能强行记下来这个公式。。。如果你一定要看一下证明,网上倒是也有一个 正态分布推导过程。
然后还有就是 C++ 库里自带了个 erf 和 erfc,大概求的是误差函数的积分和互补误差函数之类的,(我不会),有兴趣可以看看。
然后所以如果我们能够证明本题这玩意是正态分布的,那么就直接对这个 $ f(x) $ 做自适应辛普森,求一下积分就行了。
独立同分布:首先独立比较好理解,就是两个随机变量之间无影响,和高中数学里面的独立事件差不多。然后同分布就是指一些随机变量服从相同的分布。
Tips:概率论中 $ E(X) $ 表示期望,$ D(X) $ 表示方差。
中心极限定理:对于 $ n $ 个独立同分布(如本题中的相同骰子)的随机变量 $ X_1, X_2, \cdots, X_n $,若 $ E(X_i) = \mu, D(X_i) = \sigma^2 $,令:
\[Y_n = \dfrac{\sum_{i = 1}^n X_i - n\mu}{\sqrt{n\sigma^2}} \]若 $ n $ 足够大,则我们认为 $ Y_n \sim N(0, 1) $。
然后还有一个常用推论,当然首先我们需要知道正态分布的一点运算规则,即:
若 $ X \sim N(a, b) $ 则 $ cX \sim N(ca, c^2b) $,从期望和方差的意义不难理解。
若 $ X \sim N(a, b) $ 则 $ X + c \sim N(a + c, b) $,同理不难得出。
所以我们可以将刚才的中心极限定理式子转化为:
\[\sum_{i = 1}^nX_i \sim N(n\mu, n\sigma^2) \]也就是说,本题里求的这些骰子的点数和,实际上就是 $ n $ 个独立同分布的和,所以一定服从 $ N(n\mu, n\sigma^2) $,用我们刚才写的正态分布概率密度函数带进去这个期望和方差然后求个积分即可。
然后发现这东西套个自适应辛普森就可以在 $ O(\texttt{玄学}) $ 的复杂度完成。
但是我们不难发现这个东西还有点问题,就是中心极限定理需要一个前提,$ n $ 足够大,对于一些 $ n = 1 $ 之类的数据点用这个就显然寄了,所以我们要考虑一些数据点分治的做法。
显然对于 $ n $ 较小的数据,我们可以考虑多项式,多项式 $ i $ 次方项的系数为骰子值为 $ i $ 的概率,显然当 $ n = 1 $ 时,假设骰子面数为 $ m $,不难想到多项式为 $ \dfrac{1}{m}x^{m - 1} + \dfrac{1}{m}x^{m - 2} + \cdots + \dfrac{1}{m}x^1 + \dfrac{1}{m}x^0 $。然后很容易想到对于其它的 $ n $ 结果就是这个多项式的 $ n $ 次方,我们只需要用 FFT 优化一下然后在结果里求出指数在 $ [A, B] $ 之间的系数和即可,这东西可以用多项式快速幂优化(这个好像不能完全算是多项式快速幂,在正常 FFT 时写个复数的快速幂就行),我们可以分析一下,显然多项式初始项数最多为 $ m $,所以时间复杂度大概是 $ O(nm \log nm) $,常数不小,然后 $ nm $ 是 $ 4e6 $ 级别的,总之 $ nm \le 1e5 $ 应该不成问题,而且因为我们的中心极限定理一般要求 $ n \ge 30 $ 就可以了,所以这个理论上就可以过了。
Tips:仅用多项式快速幂期望得分 60~70。
然后呢会发现,这样错了,似乎是被卡精度了。。。
原因也一直没找出来,错在大数据的辛普森。能猜到的一个原因就是可能拟合 $ N(0, 1) $ 的概率密度函数会比拟合 $ N(n\mu, n\sigma^2) $ 精度更高一点?这里一直没整明白,如果有犇犇知道为什么的话欢迎私信一下,不胜感激。
总之这样会错误,我们考虑另一个方法,考虑中心极限定理的初始式子:
\[Y_n = \dfrac{\sum_{i = 1}^n X_i - n\mu}{\sqrt{n\sigma^2}} \]不难发现我们知道了限定的 $ \sum_{i = 1}^n X_i $ 的范围,也就可以带进式子里直接推出 $ Y_n $ 的范围,然后用自适应辛普森跑一下 $ N(0, 1) $ 的概率密度函数,因为 $ Y_n \sim N(0, 1) $,所以求出对应范围之后直接求 $ N(0, 1) $ 的概率密度函数在新范围里的积分即为答案。不过这样会发现依然是错误的。
检查发现,对于正态分布中,在角落可能很小,从而导致 $ [l, mid], [mid, r], [l, r] $ 都很小,从而直接返回 $ 0 $,可以感性理解一下,所以可能会导致拟合的误差过大,于是考虑每次求范围 $ [A, B] $ 的时候分别拟合 $ [0, A] $ 和 $ [0, B] $,然后用 $ [0, B] $ 的值减去 $ [0, A] $ 的,这样是等效的,且会更多的引入较大的值使得精度更高,改成此方法后才终于过了这道题。
Tips:代码中大数据自适应辛普瑟的部分注释的一些地方即为错误代码及其对应分数。
Code
#define _USE_MATH_DEFINES
#include <bits/stdc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define comp complex < ld >
#define DFT (true)
#define IDFT (false)
#define EPS (ld)(1e-10)
template < typename T = int >
inline T read(void);
int N, M;
comp comp_qpow(comp a, ll b){
comp ret(1.0, 0.0), mul(a);
while(b){
if(b & 1)ret = ret * mul;
b >>= 1;
mul = mul * mul;
}return ret;
}
class Polynomial{
private:
public:
int len;
comp A[2100000];
comp Omega(int n, int k, bool pat){
if(pat == DFT)return comp(cos(2 * PI * k / n), sin(2 * PI * k / n));
return conj(comp(cos(2 * PI * k / n), sin(2 * PI * k / n)));
}
void Reverse(comp* pol){
int pos[len + 10];
memset(pos, 0, sizeof pos);
for(int i = 0; i < len; ++i){
pos[i] = pos[i >> 1] >> 1;
if(i & 1)pos[i] |= len >> 1;
}
for(int i = 0; i < len; ++i)if(i < pos[i])swap(pol[i], pol[pos[i]]);
}
void FFT(comp* pol, int len, bool pat){
Reverse(pol);
for(int siz = 2; siz <= len; siz <<= 1)
for(comp* p = pol; p != pol + len; p += siz){
int mid = siz >> 1;
for(int i = 0; i < mid; ++i){
auto tmp = Omega(siz, i, pat) * p[i + mid];
p[i + mid] = p[i] - tmp, p[i] = p[i] + tmp;
}
}
if(pat == IDFT)
for(int i = 0; i <= len; ++i)
A[i].real(A[i].real() / (ld)len), A[i].imag(A[i].imag() / (ld)len);
}
void MakeFFT(void){
FFT(A, len, DFT);
for(int i = 0; i < len; ++i)A[i] = comp_qpow(A[i], N);
FFT(A, len, IDFT);
}
}poly;
ld mu, sigma2;
ld f(ld x){
return exp(-(x - mu) * (x - mu) / 2.0 / sigma2) / sqrt(2.0 * PI * sigma2);
}
ld Simpson(ld a, ld b){
return (b - a) * (f(a) + f(b) + 4 * f((a + b) / 2.0)) / 6.0;
}
ld Adaptive(ld l, ld r, ld cur, ld eps = 1e-6){
ld mid = (l + r) / 2.0;
ld lval = Simpson(l, mid), rval = Simpson(mid, r);
if(fabs(lval + rval - cur) <= eps * 15.0)return lval + rval + (lval + rval - cur) / 15.0;
return Adaptive(l, mid, lval, eps / 2.0) + Adaptive(mid, r, rval, eps / 2.0);
}
int main(){
int T = read();
while(T--){
M = read(), N = read();
if(N * M <= (int)1e5){
memset(poly.A, 0, sizeof poly.A);
for(int i = 0; i <= M - 1; ++i)
poly.A[i].real((ld)1.0 / (ld)M), poly.A[i].imag(0.0);
poly.len = 1;
while(poly.len <= N * M)poly.len <<= 1;
poly.MakeFFT();
for(int i = 1; i <= 10; ++i){
int A = read(), B = read();
ld ans(0.0);
for(int j = A; j <= B; ++j)ans += poly.A[j].real();
printf("%.10Lf\n", ans);
}
}else{
mu = 0.0, sigma2 = 1.0;
ld real_mu = (ld)(M - 1) / 2.0;
ld real_sig = ((ld)M * M - 1.0) / 12.0;
for(int i = 1; i <= 10; ++i){
int A = read(), B = read();
ld L = (ld)((ld)A - N * real_mu) / sqrt(N * real_sig);
ld R = (ld)((ld)B - N * real_mu) / sqrt(N * real_sig);
// WA(80pts):
// printf("%.10Lf\n", Adaptive((ld)L, (ld)R, Simpson(L, R)));
// AC:
printf("%.8Lf\n", Adaptive((ld)0, (ld)R, Simpson(0, R)) - Adaptive((ld)0, (ld)L, Simpson(0, L)));
}
// mu = (ld)N * (ld)(M - 1) / 2.0;
// sigma2 = (ld)N * (ld)((ll)M * M - 1) / 12.0;
// for(int i = 1; i <= 10; ++i){
// int A = read(), B = read();
// // WA(80pts):
// // printf("%.8Lf\n", Adaptive((ld)A, (ld)B, Simpson(A, B)));
// // WA(70pts):
// // printf("%.8Lf\n", Adaptive((ld)0, (ld)B, Simpson(0, B)) - Adaptive((ld)0, (ld)A, Simpson(0, A)));
// }
}
}
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
int flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
UPD
update-2022_12_10 初稿
标签:int,积分,拟合,mid,笔记,辛普森,dfrac,Simpson,define From: https://www.cnblogs.com/tsawke/p/17032825.html