2.4 常用的连续型分布
均匀分布
定义
如果随机变量\(X\)的密度函数为
\[f(x)= \left\{ \begin{align*} &\frac{1}{b-a},\quad\quad a\le x\le b,\\ &0,\quad\quad\quad\quad else, \end{align*} \right. \]则称\(X\)服从\([a,b]\)上的均匀分布,记作\(X\sim U[a,b]\).
性质
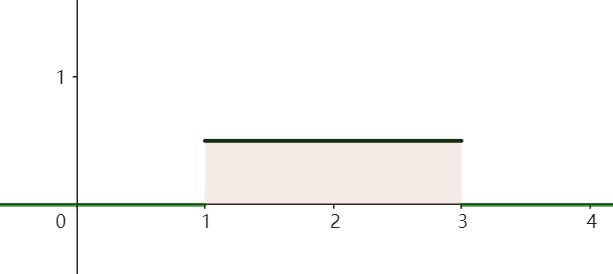
- \(\int_{-\infty}^{+\infty}f(x)dx=\int_a^bf(x)dx=1\)
矩形面积为1,因此区间\([a,b]\)上的常数必定为\(\frac{1}{b-a}\).
- 分布函数:
当\(a\le x\le b\)时,
\[\begin{align*} F(x) &= \int_{-\infty}^xf(t)dt\\ &= \int_{-\infty}^af(t)dt+\int_a^xf(t)dt\\ &= \int_a^x\frac{1}{b-a}dt\\ &= \frac{1}{b-a}\int_a^x1dt\\ &= \frac{x-a}{b-a} \end{align*} \]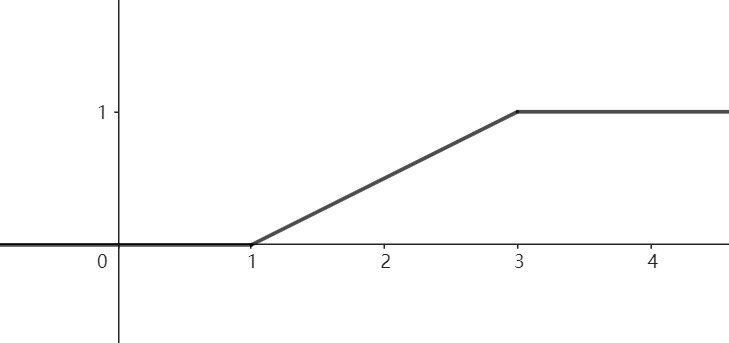
-
若\([c,d]\)是\([a,b]\)子区间,则\(P\{c\le X\le d\}=\int_c^d\frac{1}{b-a}dt=\frac{d-c}{b-a}\)。即概率与区间长度成正比。
-
数学期望:\(EX=\frac{a+b}{2}\)
证明:
\[\begin{align*} EX &= \int_{-\infty}^{+\infty}xf(x)dx\\ &= \int_a^bx\frac{1}{b-a}dx\\ &= \frac{1}{b-a}[\frac{1}{2}x^2]_a^b\\ &= \frac{1}{b-a}\times\frac{b^2-a^2}{2}\\ &= \frac{a+b}{2} \end{align*} \]- 方差:\(DX=\frac{(b-a)^2}{12}\)
简略地证明:
\[EX^2=\int_a^bx^2\frac{1}{b-a}dx=\frac{a^2+ab+b^2}{3} \]\[(EX)^2=(\frac{a+b}{2})^2=\frac{a^2+2ab+b^2}{4} \]\[DX=EX^2-(EX)^2=\frac{(a-b)^2}{12} \]相关知识点:
- \(DX=EX^2-(EX)^2\)
- 随机变量函数的数学期望(连续型):\(\int_{-\infty}^{+\infty}g(x)f(x)dx\)
- \(b^3-a^3=(b-a)(b^2+ab+a^2)\)
联系
几何概型
指数分布
定义
如果随机变量\(X\)的密度函数为
\[f(x)= \left\{ \begin{align*} &\lambda e^{-\lambda x},\quad\quad x\ge 0,\\ &0,\quad\quad\quad\quad x<0, \end{align*} \right. \]其中\(\lambda>0\)为参数,则称\(X\)服从参数为\(\lambda\)的指数分布,记作\(X\sim e(\lambda)\).
分布函数
\[F(x)= \left\{ \begin{align*} &1-e^{-\lambda x},\quad\quad x\ge 0,\\ &0,\quad\quad\quad\quad x<0, \end{align*} \right. \]数学期望
\[EX=\frac{1}{\lambda} \]方差
\[DX=\frac{1}{\lambda^2} \]性质
- 无记忆性:\(P\{X>r+s|X>s\}=P\{X>r\}\)
联系
-
指数分布与泊松分布之间的联系:
如果用参数为\(\lambda\)的泊松分布描述单位时间事件发生的次数,那么一次事件发生的等待时间便服从参数为\(\lambda\)的指数分布。
-
指数分布与几何分布之间的联系:
- 指数分布描述事件发生等待的时间(连续量)
- 几何分布描述事件发生等待的次数(离散量)
正态分布
定义
如果随机变量\(X\)的密度函数为
\[\varphi(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad-\infty<x<+\infty, \]其中\(\mu,\sigma\)为常数,且\(\sigma>0\),则称\(X\)服从参数为\(\mu\)和\(\sigma^2\)的正态分布,记作\(X\sim N(\mu,\sigma^2)\).
分布函数
由于密度函数的原函数没有解析表达式,因而其分布函数(记作\(\varPhi(x)\))不能表示为解析式。
\[\varPhi(x)=\int_{-\infty}^x\varphi(t)dt=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^xe^{-\frac{(t-\mu)^2}{2\sigma^2}}dt \]性质
- \(\int_{-\infty}^{+\infty}\varphi(x)dx=1\).
证明:
前置知识点:根据欧拉-泊松积分,有\(\int_{-\infty}^{+\infty}e^{-x^2}dx=\sqrt{\pi}\)
标签:infty,frac,int,连续型,mu,数理统计,quad,sigma,2.4 From: https://www.cnblogs.com/feixianxing/p/common-continuous-distribution.html