标签：直线 方程 BC AC 当且 斜率 寒假 数学 2023

2021级高二寒假数学作业（一）　直线 与 方 程

单选题

01.C

02.A

03.B

04.C

---

多选题

01.A,B,D

02.A,C,D

---

填空题

01.

x－y＋2＝0

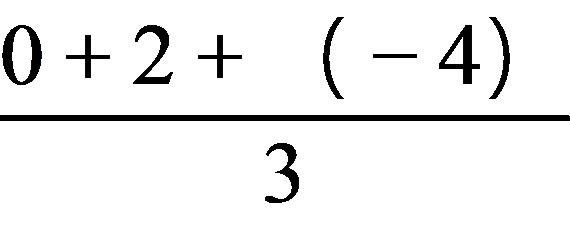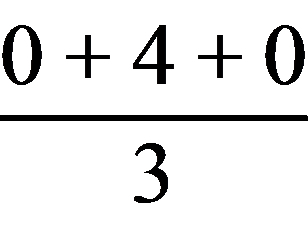设△ABC的重心为G，垂心为H.由重心坐标公式得x＝​​＝－​​，y＝​​＝​​，所以G(－​​，​​).由题知，△ABC的边AC上的高线所在直线方程为x＝0，直线BC：y＝x＋4，A(2，0)，所以△ABC的边BC上的高线所在直线方程为y＝－x＋2，所以​​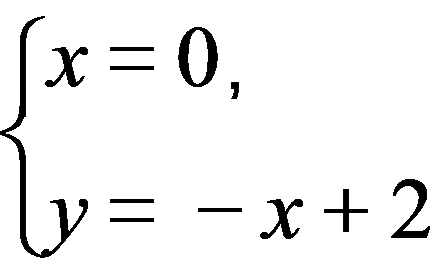⇒H(0，2)，所以欧拉线GH的方程为x－y＋2＝0.

02.

(​​，​​)

因为PA＋PC≥AC，当且仅当点A，P，C三点共线，且点P位于A，C之间时等号成立，PB＋PD≥BD，当且仅当B，P，D三点共线，且点P位于B，D之间时等号成立，所以PA＋PB＋PC＋PD≥AC＋BD，当且仅当P为直线AC与BD的交点时等号成立．因为A(－1，0)，B(1，0)，C(2，3)，D(－2，6)，所以直线AC的方程为x－y＋1＝0，直线BD的方程为2x＋y－2＝0，所以直线AC与BD的交点为(​​，​​)，所以当点P的坐标为(​​，​​)时，PA＋PB＋PC＋PD取最小值．

​​

---

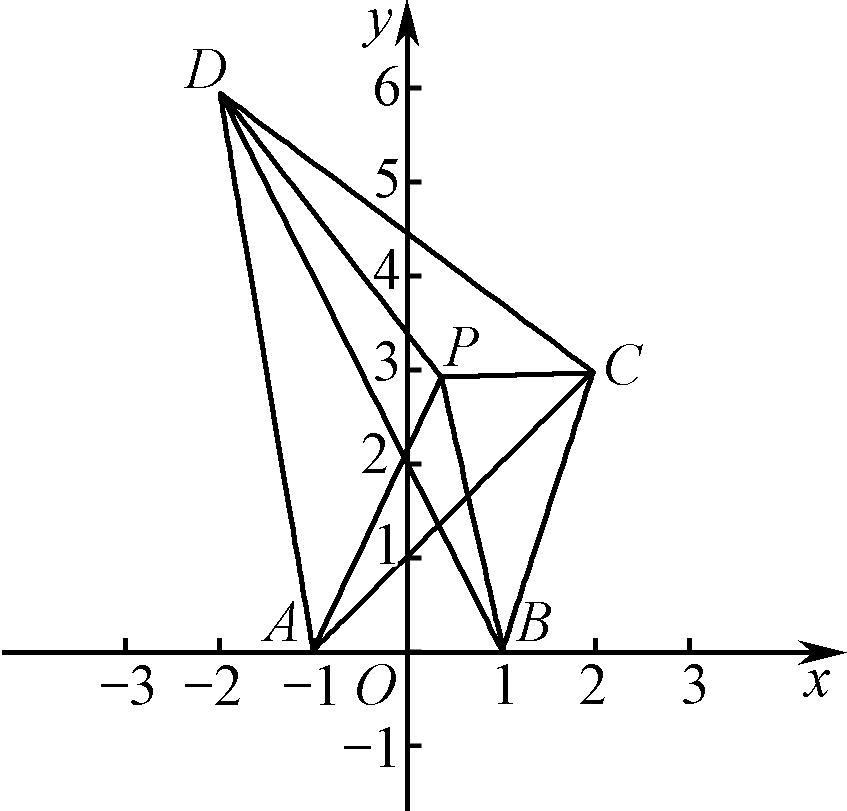
解答题

01.

(1) ∵ B(－1，－2)，C(6，3)，直线BC的斜率k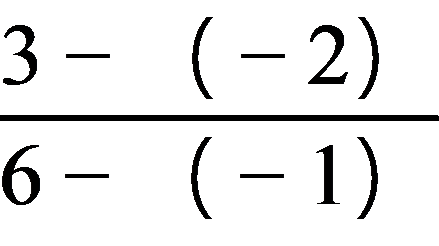＝​​＝​​，故边BC上的高线所在直线的斜率k₁＝－​​，故边BC上的高线所在直线的方程为y－6＝－​​(x－1)，即7x＋5y－37＝0.

(2) BC的中点D(​​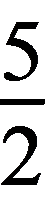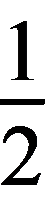，​​)，中线AD所在直线的斜率k₂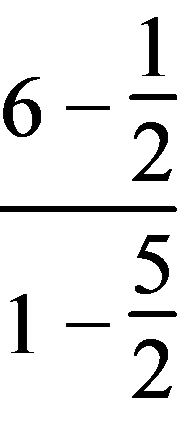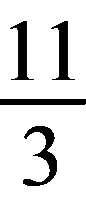＝​​＝－​​，故边BC上的中线AD所在直线的方程为y－6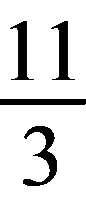＝－​​(x－1)，即11x＋3y－29＝0.

02.

(1) 由已知得直线l斜率存在，设l：y＝kx－1(k>0).

由​​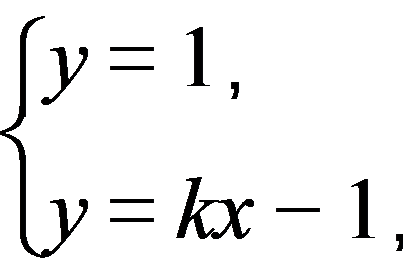得M(​​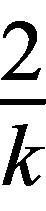，1).又0<​​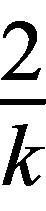<1，所以k>2.

由​​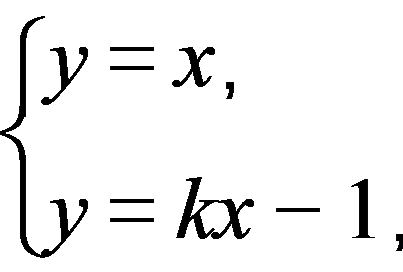得N(​​，​​).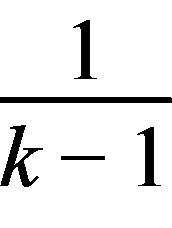

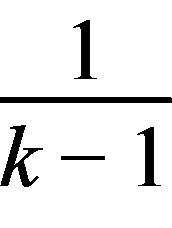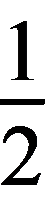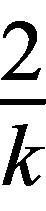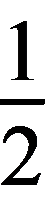(2) S＝S_△OPM－S_△OPN＝​​×1×​​－​​×1×​​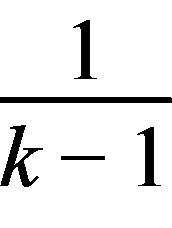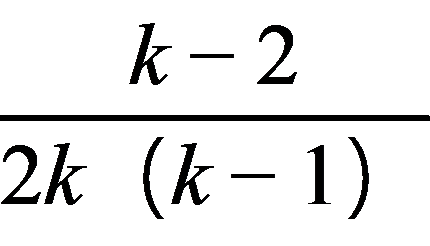＝​​(k>2).

(3) 设t＝k－2，则t>0，

S＝​​＝​​≤​​＝​​，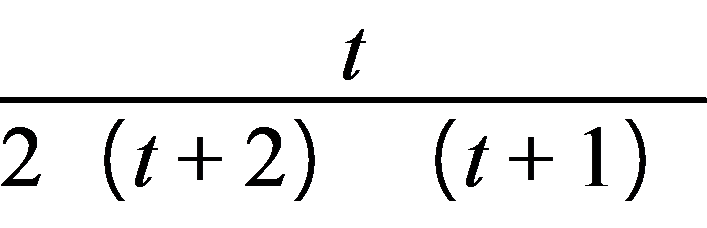

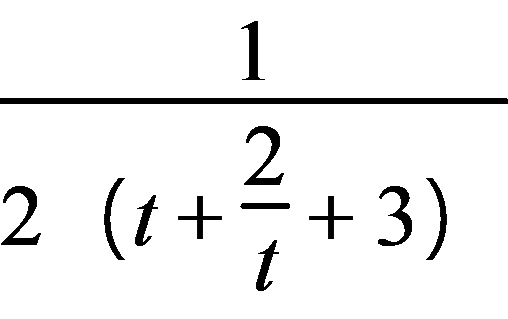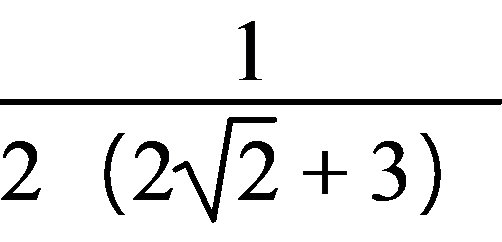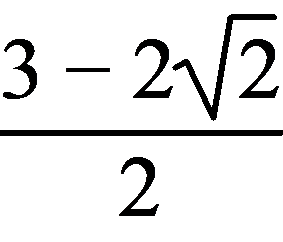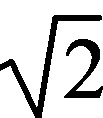当且仅当t＝​​⇒t＝​​⇒k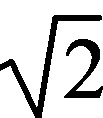＝​​＋2时，等号成立，此时S取得最大值​​.

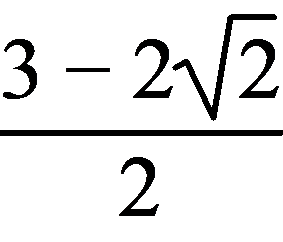03.

(1) 因为过点P(1，2)作直线l分别与x，y轴正半轴交于点A，B，且△AOB是等腰直角三角形，

所以直线l的倾斜角为​​，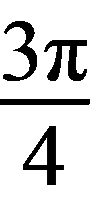

所以直线l的斜率k＝tan ​​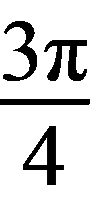＝－1，

所以直线l的方程为y－2＝－(x－1)，即x＋y－3＝0.

(2) 设A(a，0)，B(0，b)(a，b>0)，直线l的方程为​​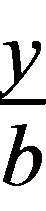＋​​＝1，代入点P(1，2)可得​​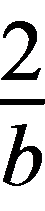＋​​＝1.

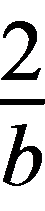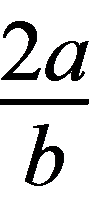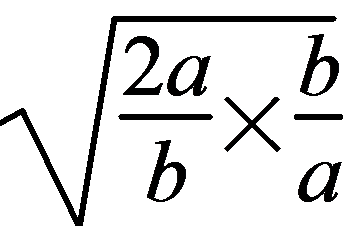若选①：OA＋OB＝a＋b＝(a＋b)(​​＋​​)＝3＋​​＋​​≥3＋2​​＝3＋2​​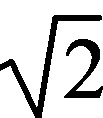，当且仅当a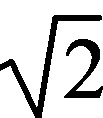＝​​＋1，b＝2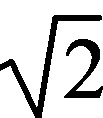＋​​时等号成立，此时直线l的斜率k＝－​​＝－​​，

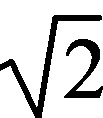所以直线l的方程为y－2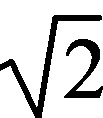＝－​​(x－1)，即​​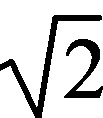x＋y－2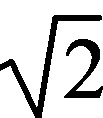－​​＝0；

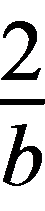若选②：由​​＋​​＝1≥2​​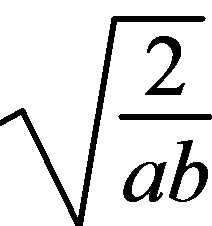，可得ab≥8，当且仅当a＝2，b＝4时等号成立，

所以S_△AOB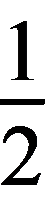＝​​ab≥4，即△AOB的面积最小为4，此时直线l的斜率k＝－​​＝－2，

所以直线l的方程为y－2＝－2(x－1)，即2x＋y－4＝0.

---

标签：直线,方程,BC,AC,当且,斜率,寒假,数学,2023
From： https://www.cnblogs.com/luoyj506/p/17007929.html