\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019)]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性第二册同步巩固,难度2颗星!
基础知识
极值的概念
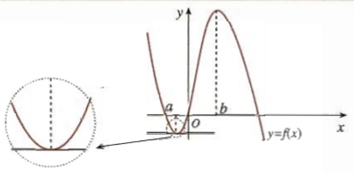
若在点\(x=a\)附近的左侧\(f'(x)<0\),右侧\(f'(x)>0\), 则\(a\)称为函数\(y=f(x)\)的极小值点,\(f(a)\)称为函数\(y=f(x)\)的极小值;
若在点\(x=b\)附近的左侧\(f'(x)>0\),右侧\(f'(x)<0\),则\(b\)称为函数\(y=f(x)\)的极大值点,\(f(b)\)称为函数\(y=f(x)\)的极大值.
极小值点、极大值点统称为极值点,极大值和极小值统称为极值.
解释
① 把函数图象看成一座“山脉”,极大值就是“山峰”,极小值就是“山谷”, 如下图;
② 极值是“函数值\(y\)”,极值点是“自变量\(x\)值”,如下图有极大值\(f(-1)\)和\(f(1)\),极小值\(f(-2)\)和\(f(2)\),极大值点\(-1\)和\(1\),极小值点\(-2\)和\(2\).

③ 极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质;
④ 对于极值还有特别强调一下,看例题:
【例】设\(x_0\)是函数\(y=f(x)\)的极值点,则下列说法准确的是( )
A. 必有\(f'(x_0 )=0\) \(\qquad \qquad \qquad \qquad\qquad \qquad\) B.\(f'(x_0 )\)不存在
C. \(f'(x_0 )=0\)或\(f'(x_0 )\)不存在 \(\qquad \qquad \qquad \qquad\) D. \(f'(x_0 )\)存在但可能不为\(0\)
解析 函数\(f(x)=x^3\),

\(f'(x)=3x^2\),\(f'(0)=0\),
但\(x<0\)时,\(f'(x)>0\);\(x>0\)时,\(f'(x)>0\);
故根据极值的定义,\(0\)不是函数\(f(x)=x^3\)的极值点,这个从函数图象也很容易知道.
又如函数\(g(x)=|x|\),

当\(x<0\)时,\(g'(x)=-1<0\); 当\(x>0\)时,\(g'(x)=1>0\);
所以\(g(x)\)在\(x=0\)处取到极值,但在导数不存在;故选\(C\).
总结
① 若\(f(x)\)可导,且\(x_0\)是\(y=f(x)\)的极值,则\(x_0\)是\(f'(x)=0\)的解;
② 若\(x_0\)是\(f'(x)=0\)的解,\(x_0\) 不一定是\(y=f(x)\)的极值点;
③ 定义很重要.
【例】判断\(x=0\)是否\(f(x)= \dfrac{1}{3} x^3-x^2\)的极大值点.
解 \(\because f(x)= \dfrac{1}{3} x^3-x^2\),\(\therefore f'(x)=x^2-2x\),
当\(x>0\)时,\(f'(x)<0\);当\(x<0\)时,\(f'(x)>0\);
所以\(x=0\)是\(f(x)= \dfrac{1}{3} x^3-x^2\)的极大值点.
求函数的极值的方法
解方程\(f'(x)=0\) ,当\(f'(x_0)=0\)时:
(1) 如果在\(x_0\)附近的左侧\(f'(x)>0\),右侧\(f'(x)<0\),那么\(f(x_0)\)是极大值;
(2) 如果在\(x_0\)附近的左侧\(f'(x)<0\),右侧 \(f'(x)>0\),那么\(f(x_0)\)是极小值.
基本方法
【题型1】 极值的概念
【典题1】(多选)设函数\(f(x)\)的定义域为\(R\),\(x_0 (x_0≠0)\)是\(f(x)\)的极大值点,以下结论错误的是( )
A.\(∀x∈R\),\(f(x)≤f(x_0)\) \(\qquad \qquad \qquad \qquad \qquad\) B.\(-x_0\)是\(f(-x)\)的极小值点
C.\(-x_0\)是\(-f(x)\)的极小值点 \(\qquad \qquad \qquad \qquad\) D.\(-x_0\)是\(-f(-x)\)的极小值点
解析 \(A\).\(∀x∈R\),\(f(x)≤f(x_0)\),错误.\(x_0 (x_0≠0)\)是\(f(x)\))的极大值点,并不是最大值点;
\(B\).\(-x_0\)是\(f(-x)\)的极小值点,错误.\(f(-x)\)相当于\(f(x)\)关于\(y\)轴的对称图象,故\(-x_0\)应是\(f(-x)\)的极大值点;
\(C\).\(-x_0\)是\(-f(x)\)的极小值点,错误.\(-f(x)\)相当于\(f(x)\)关于\(x\)轴的对称图象,故\(x_0\)应是\(-f(x)\)的极小值点.跟\(-x_0\)没有关系;
\(D\).\(-x_0\)是\(-f(-x)\)的极小值点,正确.\(-f(-x)\)相当于\(f(x)\)先关于\(y\)轴的对称,再关于\(x\)轴的对称图象.故\(D\)正确.
故选:\(ABC\).
点拨 结合图象分析.
【典题2】若函数 \(f(x)=x^3-\left(\dfrac{a}{2}+3\right) x^2+2 a x+3\)在\(x=2\)处取得极小值,则实数\(a\)的取值范围是( )
A.\((-∞,-6)\) \(\qquad \qquad \qquad\) B.\((-∞,6)\) \(\qquad \qquad \qquad\) C.\((6,+∞)\) \(\qquad \qquad \qquad\) D.\((-6,+∞)\)
解析 \(f(x)=x^3-\left(\dfrac{a}{2}+3\right) x^2+2 a x+3\),
则\(f'(x)=3x^2-(a+6)x+2a\),
由题意得:\(f'(2)=0\),即\(12-2a-12+2a=0\),\(f'(2)\)恒为\(0\),
\(\because f(2)\)是极小值,\(\therefore x<2\)时,函数单调递减,\(x>2\)时,函数单调递增,
结合二次函数的性质\(f'(x)\)的对称轴在\(x=2\)的左侧,
即\(\dfrac{a+6}{6}<2\),故\(a<6\),
又\(△=(a+6)^2-24a=(a-6)^2>0\),故\(a<6\),
故选:\(B\).
点拨 本题依题意得\(f'(2)=0\),由于等式恒成立,求不出\(a\),则利用极值的概念求出\(a\)的取值范围.
【巩固练习】
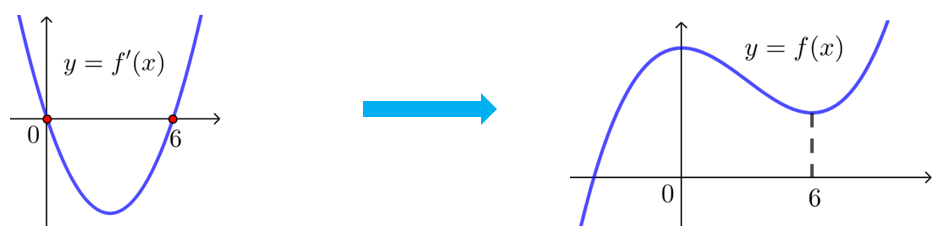
1.已知函数\(y=f(x)\)的导函数的图象如图所示,则下列结论正确的是( )

A.\(-4\)是函数\(f(x)\)的极小值点 \(\qquad \qquad \qquad \qquad\) B.\(-1\)是函数\(f(x)\)的极小值点
C.函数\(f(x)\)在区间\((-4,1)\)上单调递减 \(\qquad \qquad\) D.函数\(f(x)\)在区间\((-4,-1)\)上先增后减
2.函数\(f(x)=4x^3-ax^2-2bx+2\)在\(x=1\)处有极值,则\(a+b\)的值等于( )
A.\(9\) \(\qquad \qquad \qquad \qquad\) B.\(6\) \(\qquad \qquad \qquad \qquad\) C.\(3\) \(\qquad \qquad \qquad \qquad\) D.\(2\)
3.已知函数\(f(x)=x^3+2ax^2+bx+a^2\)在\(x=1\)处的极小值为\(6\),则数对\((a,b)\)为( )
A.\((-2,5)\) \(\qquad \qquad\) B.\((-19,4)\) \(\qquad \qquad\) C.\((4,-19)\) \(\qquad \qquad\) D.\((-2,5)\)或\((4,-19)\)
4.(多选)已知函数\(f(x)= \dfrac{1}{3} x^3+x^2-2ax+1\),当实数\(a\)为下列( )的值时,函数\(f(x)\)在\((1,2)\)上有极值.
A.\(1\) \(\qquad \qquad \qquad \qquad\) B.\(2\)\(\qquad \qquad \qquad \qquad\) C.\(3\) \(\qquad \qquad \qquad \qquad\) D.\(4\)
参考答案
-
答案 \(A\)
解析 结合导函数的图象,可知\(f(x)\)在\((-∞,-4)\)单调递减,在\((-4,+∞)\)单调递增,
所以\(-4\)是函数\(f(x)\)的极小值点,故\(A\)正确;
\(-1\)不是\(f(x)\)的极值点,故\(B\)错误;
函数\(f(x)\)在区间\((-4,1)\)上单调递增,故\(C\)错误;
函数\(f(x)\)在区间\((-4,-1)\)上单调递增,故\(D\)错误;
故选:\(A\). -
答案 \(B\)
解析 函数\(f(x)=4x^3-ax^2-2bx+2\)在\(x=1\)处有极值,可知\(f'(1)=0\),
而\(f'(x)=12x^2-2ax-2b\),故\(12-2a-2b=0\) ,故\(a+b=6\),
故选:\(B\). -
答案 \(C\)
解析 由\(f(x)=x^3+2ax^2+bx+a^2\),得\(f'(x)=3x^2+4ax+b\),
\(\because f(x)\)在\(x=1\)处的极小值为\(6\),\(\therefore f'(1)=0\)且\(f(1)=6\),
\(\therefore 3+4a+b=0\)且\(1+2a+b+a^2=6\),
\(\therefore a=-2\),\(b=5\)或\(a=4\),\(b=-19\),
经检验当\(a=-2\),\(b=5\)时,\(f(x)\)在\(x=1\)处取不到极小值\(6\),
\(\therefore a=4\),\(b=-19\), \(\therefore\)数对\((a,b)\)为\((4,-19)\).
故选:\(C\). -
答案 \(BC\)
解析 \(f'(x)=x^2+2x-2a\),
因为函数\(f(x)\)在\((1,2)\)上有极值,所以\(f'(x)=0\)在\((1,2)\)上有根,
所以\(y=f'(x)\)在\((1,2)\)上有变号零点,
又因为\(f'(x)=x^2+2x-2a\),在\((1,2)\)上单调递增,
所以\(\left\{\begin{array}{l} f^{\prime}(1)=3-2 a<0 \\ f^{\prime}(2)=8-2 a>0 \end{array}\right.\),解得\(\dfrac{3}{2}<a<4\),
故选:\(BC\).
【题型2】 不含参函数的极值
【典题1】 已知曲线\(f(x)=ax^3-bx^2+2\)在点\((1,f(1))\)处的切线方程为\(y=1\).
(1)求\(a\)、\(b\)的值;\(\qquad \qquad\) (2)求\(f(x)\)的极值.
解析 (1)由函数的解析式可得\(f'(x)=3ax^2-2bx\),
由切线方程可知切点坐标为\((1,1)\),切线的斜率为\(0\),
从而有 \(\left\{\begin{array}{l}
f(1)=a-b+2=0 \\
f^{\prime}(1)=3 a-2 b=0
\end{array}\right.\),求解方程组可得 \(\left\{\begin{array}{l}
a=2 \\
b=3
\end{array}\right.\),
故\(a=2\),\(b=3\).
(2)由题意可得\(f(x)=2x^3-3x^2+2\),\(f'(x)=6x^2-6x\),
当\(x∈(-∞,0)\)时,\(f'(x)>0\),\(f(x)\)单调递增,
当\(x∈(0,1)\)时,\(f'(x)<0\),\(f(x)\)单调递减,
当\(x∈(1,+∞)\)时,\(f'(x)>0\),\(f(x)\)单调递增,
故函数的极大值为\(f(0)=2\),函数的极小值为\(f(1)=1\).
点拨 求函数极值先求函数单调性,解题步骤与思路差不多;借助导函数的“穿线图”更好得到结论.
【巩固练习】
1.下列函数中,不存在极值点的是( )
A.\(y=x+ \dfrac{1}{x}\) \(\qquad \qquad\) B. \(y=2^{|x|}\) \(\qquad \qquad\) C.\(y=x⋅\ln x\) \(\qquad \qquad\) D.\(y=-2x^3-x\)
2.函数\(y=1+3x-x^3\)有( )
A.极小值\(-1\),极大值\(1\) \(\qquad \qquad \qquad \qquad\) B.极小值\(-1\),极大值\(3\)
C.极小值\(-2\),极大值\(2\) \(\qquad \qquad \qquad \qquad\) D.极小值\(2\),极大值\(3\)
3.函数\(f(x)=\cos 2x+\sin x\),\(x \in\left(0, \dfrac{\pi}{2}\right)\)的极值点为\(x_0\),则\(\tan x_0\)的值为( )
A.\(\dfrac{\sqrt{15}}{15}\) \(\qquad \qquad \qquad \qquad\) B.\(\sqrt{15}\) \(\qquad \qquad \qquad \qquad\) C.\(\sqrt{3}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{\sqrt{3}}{3}\)
4.已知函数\(f(x)=a\ln x- \dfrac{1}{2} x^2\),\((a∈R)\)在\(x=1\)处的切线与直线\(y=x+1\)平行.
(1)求实数a的值;\(\qquad \qquad\) (2)求函数\(f(x)\)的极值.
参考答案
-
答案 \(D\)
解析 \(y=x+ \dfrac{1}{x}\),\(x=-1\)时,函数取得极大值,\(x=1\)时,函数取得极小值,所以\(A\)不正确;
\(y=2^{|x|}\)是偶函数,\(x=0\)时,函数取得极小值,所以\(B\)不正确;
\(y=x⋅\ln x\)可得\(y'=\ln x+1\), \(x>\dfrac{1}{e}\)时,\(y'>0\),函数是增函数,
\(x \in\left(0, \dfrac{1}{e}\right)\)时,\(y'<0\),函数是减函数,\(x=\dfrac{1}{e}\)时,函数取得极小值,所以\(C\)不正确.
\(y=-2x^3-x\),可得\(y'=-6x^2-1<0\)恒成立,函数是减函数,
所以函数没有极小值,所以\(D\)正确.
故选:\(D\). -
答案 \(B\)
解析 \(y'=3-3x^2\),
令\(y'=0\),解得\(x=±1\),
\(x∈(-∞,-1)\),\((1,+∞)\)时,\(y'<0\),\(x∈(-1,1)\)时,\(y'>0\),
\(\therefore\)函数\(y=1+3x-x^3\)有在\((-∞,-1)\),\((1,+∞)\)上递减,在\((-1,1)\)递增,
\(\therefore x=1\),函数取得极大值\(1+3×1-1^3=3\),
\(x=-1\)时,函数取得极小值\(1+3×(-1)-(-1)^3=-1\),
故选:\(B\). -
答案 \(A\)
解析 函数\(f(x)=\cos 2x+\sin x\),\(x \in\left(0, \dfrac{\pi}{2}\right)\),
所以 \(f^{\prime}(x)=-2 \sin 2 x+\cos x=\cos x(1-4 \sin x)\),
令\(f'(x)=0\),\(\cos x(1-4\sin x)=0\),
因为\(x \in\left(0, \dfrac{\pi}{2}\right)\),所以\(\cos x≠0\),
所以\(1-4\sin x=0\),即\(\sin x= \dfrac{1}{4}\),
因为函数\(f(x)=\cos 2x+\sin x\),\(x \in\left(0, \dfrac{\pi}{2}\right)\)的极值点为\(x_0\),
所以\(\sin x_0= \dfrac{1}{4}\), \(\cos x_0=\dfrac{\sqrt{15}}{4}\), \(\therefore \tan x_0=\dfrac{\sqrt{15}}{15}\),
故选:\(A\). -
答案 (1) \(a=2\);(2) 极大值为\(\ln 2-1\),无极小值.
解析 (1)由题意可知,\(f'(1)=1\),
\(\because f^{\prime}(x)=\dfrac{a}{x}-x\),\(\therefore f'(1)=a-1=1\),\(\therefore a=2\).
(2) \(\because f^{\prime}(x)=\dfrac{2}{x}-x=\dfrac{2-x^2}{x}\),
\(\therefore f'(x)>0⇒0<x<\sqrt{2}\),\(f'(x)<0⇒x>\sqrt{2}\),
即函数\(f(x)\)在\((0,\sqrt{2})\)上单调递增,在\((\sqrt{2},+∞)\)上单调递减,
故函数\(f(x)\)的极大值为\(f(\sqrt{2})=2\ln \sqrt{2}-1=\ln 2-1\),无极小值.
【题型3】含参函数的极值
【典题1】讨论函数\(f(x)=e^x-2ax-a\)的极值.
解析 \(f'(x)=e^x-2a\),
当\(a≤0\)时,\(f'(x)= e^x-2a>0\),\(f(x)\)在\(R\)上为单调增函数,无极值,
当\(a>0\)时,
由\(f'(x)= e^x-2a>0\),\(x>\ln (2a)\),\(f(x)\)在\((\ln (2a),+∞)\)上为单调增函数,
由\(f'(x)= e^x-2a<0\),\(x<\ln (2a)\),\(f(x)\)在\((-∞,\ln (2a))\)上为单调减函数,
所以 \(f_{\text {极小值 }}=f(\ln (2 a))=a-2 a \ln (2 a)\),无极大值.
综上所述:当\(a≤0\)时,无极值,
当\(a>0\)时, \(f_{\text {极小值 }}=a-2 a \ln (2 a)\),无极大值.
【巩固练习】
1.讨论\(f(x)=x^3-ax^2+2\)的极值.
2.讨论\(f(x)=\ln x+ \dfrac{1}{2} x^2+ax(a∈R)\)的极值点的个数.
参考答案
-
答案 当\(a≤0\)时,\(f(x)\)无极值;当\(a>0\)时,极小值\(-\dfrac{4 a^3}{27}+2\),无极大值.
解析 定义域\(x∈(0,+∞)\),\(f'(x)=3x^2-2ax=x(3x-2a)\),
当\(a≤0\)时,\(f'(x)≥0\),\(f(x)\)在\((0,+∞)\)上单增,无极值,
当\(a>0\)时, \(f^{\prime}(x)>0 \Rightarrow x>\dfrac{2 a}{3}\),
\(\therefore f(x)\)单减区间是\(\left(0, \dfrac{2 a}{3}\right)\),单增区间是\(\left(\dfrac{2 a}{3},+\infty\right)\),
所以 \(f(x)_{\text {极小 }}=f\left(\dfrac{2 a}{3}\right)=-\dfrac{4 a^3}{27}+2\),无极大值.
综上所述,当\(a≤0\)时,\(f(x)\)无极值;当\(a>0\)时,极小值\(-\dfrac{4 a^3}{27}+2\),无极大值. -
答案 当\(a≥-2\)时,函数\(f(x)\)无极值点;当\(a<-2\)时,\(f(x)\)有两个极值点.
解析 由题意得: \(f^{\prime}(x)=\dfrac{1}{x}+x+a=\dfrac{x^2+a x+1}{x}(x>0)\),
令\(f'(x)=0\),即\(x^2+ax+1=0\),\(△=a^2-4\),
①当\(△=a^2-4≤0\),即\(-2≤a≤2\)时,
\(x^2+ax+1≥0\)对任意的\(x>0\)恒成立,
即\(f^{\prime}(x)=\dfrac{x^2+a x+1}{x} \geq 0\)对任意\(x>0\)恒成立,此时\(f(x)\)没有极值点;
②当\(△=a^2-4>0\),即\(a<-2\)或\(a>2\)时,
若\(a<-2\),设方程的两根不同实根\(x_1\),\(x_2\),
不妨设\(x_1<x_2\),
则\(x_1+x_2=-a\),\(x_1 x_2=1>0\),故\(x_2>x_1>0\),
当\(0<x<x_1\) 或\(x>x_2\)时,\(f'(x)>0\),
当\(x_1<x<x_2\)时,\(f'(x)<0\),
故\(x_1\),\(x_2\)是函数\(f(x)\)的两个极值点.
若\(a>2\),设方程\(x^2+ax+1=0\)的两个不同的实根\(x_1\),\(x_2\),
则\(x_1+x_2=-a<0\),\(x_1 x_2=1\),故\(x_1<0\),\(x_2<0\),
所以当\(x>0\)时,\(f'(x)>0\),故函数\(f(x)\)没有极值点,
综上当\(a≥-2\)时,函数\(f(x)\)无极值点;当\(a<-2\)时,\(f(x)\)有两个极值点.
分层练习
【A组---基础题】
1.已知函数\(f(x)\)的导函数为\(f'(x)\),函数\(g(x)=(x-1)f'(x)\)的图象如图所示,则下列结论正确的是( )

A.\(f(x)\)在\((-∞,-2)\),\((1,2)\)上为减函数 \(\qquad \qquad \qquad \qquad\) B.\(f(x)\)在\((-2,1)\),\((2,+∞)\)上为增函数
C.\(f(x)\)的极小值为\(f(-2)\),极大值为\(f(2)\) \(\qquad \qquad \qquad \qquad\) D.\(f(x)\)的极大值为\(f(-2)\),极小值为\(f(2)\)
2.函数\(f(x)= \dfrac{1}{2} x^2+\ln x-2x\)的极值点的个数是( )
A.\(0\) \(\qquad \qquad \qquad \qquad\) B.\(1\) \(\qquad \qquad \qquad \qquad\) C.\(2\) \(\qquad \qquad \qquad \qquad\) D.无数个
3.若函数\(f(x)= \dfrac{1}{2} x^2-x+a\ln x\)有两个不同的极值点,则实数\(a\)的取值范围是( )
A.\(a> \dfrac{1}{4}\) \(\qquad \qquad \qquad\) B.\(- \dfrac{1}{4}<a<0\) \(\qquad \qquad \qquad\) C.\(a< \dfrac{1}{4}\) \(\qquad \qquad \qquad\) D.\(0<a< \dfrac{1}{4}\)
4.已知函数\(f(x)=x\ln x+x^2\),且\(x_0\)是函数\(f(x)\)的极值点.给出以下几个问题:
①\(x_0> \dfrac{1}{e}\);②\(0<x_0< \dfrac{1}{e}\);③\(f(x_0 )+x_0<0\);④\(f(x_0 )+x_0>0\)
其中正确的命题是( )
A.①③ \(\qquad \qquad \qquad \qquad\) B.①④ \(\qquad \qquad \qquad \qquad\) C.②③ \(\qquad \qquad \qquad \qquad\) D.②④
5.已知函数\(f(x)=x^3+3ax^2+1(a<0)\),\(f(x)\)极小值点为\(x_0\),若\(f(x_1 )=f(x_0 )\)且\(x_1≠x_0\),则\(x_1⋅f(x_1+x_0 )\)的最小值为( )
A.\(- \dfrac{3}{4}\) \(\qquad \qquad \qquad \qquad\) B. \(- \dfrac{3}{8}\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{3}{8}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{3}{4}\)
6.若函数\(f(x)=m\cdot e^x-x^2+2x(m<0)\)在\((0,1)\)上有极值点,则\(m\)的取值范围为\(\underline{\quad \quad}\).
7.设\(x_1\)和\(x_2\)是函数\(f(x)=x^3+2ax^2+x+1\)的两个极值点.若\(x_2-x_1=2\),则\(a^2=\)\(\underline{\quad \quad}\).
8.设函数\(f(x)=2x^3+3x^2+ax+b\),曲线\(y=f(x)\)在点\((0,f(0))\)处的切线方程为\(y=-12x+1\).
(1)求\(f(x)\)的解析式;\(\qquad \qquad\) (2)求\(f(x)\)的极值.
9.设\(a\)为实数,函数\(f(x)= \dfrac{1}{3} x^3- \dfrac{1}{2}(a-1)x^2-ax(x∈R)\).
(1)当\(a=1\)时,求\(f(x)\)的单调区间;
(2)求\(f(x)\)在\(R\)上的极大值与极小值.
参考答案
-
答案 \(D\)
解析 当\(x∈(-∞,-2)\)时,\(x-1<0\),由图象可得\(g(x)=(x-1)f'(x)<0\),
则\(f'(x)>0\),\(f(x)\)为增函数;
当\(x∈(-2,1)\)时,\(x-1<0\),由图象可得\(g(x)=(x-1)f'(x)>0\),
则\(f'(x)<0\),\(f(x)\)为减函数;
当\(x∈(1,2)\)时,\(x-1>0\),由图象可得\(g(x)=(x-1)f'(x)<0\),
则\(f'(x)<0\),\(f(x)\)为减函数;
当\(x∈(2,+∞)\)时,\(x-1>0\),由图象可得\(g(x)=(x-1)f'(x)>0\),
则\(f'(x)>0\),\(f(x)\)为增函数,
所以\(f(x)\)的极大值为\(f(-2)\),极小值为\(f(2)\),
结合选项可知,只有选项\(D\)正确.
故选:\(D\). -
答案 \(A\)
解析 \(f^{\prime}(x)=x+\dfrac{1}{x}-2=\dfrac{(x-1)^2}{x} \geqslant 0\),
故原函数单调递增,\(f(x)\)无极值点.
故选:\(A\). -
答案 \(D\)
解析 因为\(f(x)= \dfrac{1}{2} x^2-x+a\ln x\)有两个不同的极值点,
所以\(f^{\prime}(x)=x-1+\dfrac{a}{x}=\dfrac{x^2-x+a}{x}=0\)在\((0,+∞)\)有\(2\)个不同的零点,
所以\(x^2-x+a=0\)在\((0,+∞)\)有\(2\)个不同的零点,
所以\(\left\{\begin{array}{l} \triangle=1-4 a>0 \\ a>0 \end{array}\right.\),解可得,\(0<a< \dfrac{1}{4}\).
故选:\(D\). -
答案 \(C\)
解析\(f(x)\)的定义域为\(x>0\),\(f'(x)=\ln x+2x+1\),
所以有$f'(x_0 )=\ln x_0+2x_0+1=$0,
所以有\(2x_0=-(\ln x_0+1)>0\),即\(\ln x_0<-1\),
即 \(\ln x_0<\ln e^{-1}\),所以有\(0<x_0< \dfrac{1}{e}\);故①错误,②正确;
\(f(x_0 )+x_0=x_0 \ln x_0+x_0^2+x_0=x_0 (\ln x_0+x_0+1)\),
因为\(2x_0=-(\ln x_0+1)\),
所以有\(f(x_0 )+x_0=x_0 \ln x_0+x_0^2+x_0=x_0 (\ln x_0+x_0+1)=-x_0^2<0\),
故③正确,④错误.
故选:\(C\). -
答案 \(B\)
解析 \(f'(x)=3x^2+6ax=3x(x+2a)\),
\(\because a<0\),
当\(x>-2a\)或\(x<0\)时,\(f'(x)>0\),函数单调递增,
当\(0<x<-2a\)时,\(f'(x)<0\),函数单调递减,
故极小值点为\(x_0=-2a\),
由\(f(x_1 )=f(x_0 )=1+4a^3\)可得\(x_1=a\),
则\(x_1⋅f(x_1+x_0 )=af(-a)=a(2a^3+1)=2a^4+a\),
设\(g(a)=2a^4+a(a<0)\),\(g'(a)=8a^3+1\),
当\(a \in\left(-\infty,-\dfrac{1}{2}\right)\),\(g'(a)<0\); \(a \in\left(-\dfrac{1}{2},+\infty\right)\),\(g'(a)>0\)
所以\(g(a)\)在\(\left(-\infty,-\dfrac{1}{2}\right)\)上单调递减,在\(\left(-\dfrac{1}{2},+\infty\right)\)上单调递增,
故\(g(a)_{\min }=g\left(-\dfrac{1}{2}\right)=-\dfrac{3}{8}\).
故选:\(B\). -
答案 \((-2,0)\)
解析 \(f'(x)=m\cdot e^x-2x+2(m<0)\),
所以\(f'(x)\)在\((0,1)\)上为减函数,
所以\(\left\{\begin{array}{l} f^{\prime}(0)=m+2>0 \\ f^{\prime}(1)=m e<0 \end{array}\right.\),解得\(-2<m<0\),
故答案为:\((-2,0)\). -
答案 \(3\)
解析 \(\because\)函数\(f(x)=x^3+2ax^2+x+1\), \(\therefore f'(x)=3x^2+4ax+1\),
又\(x_1\)和\(x_2\)是函数\(f(x)=x^3+2ax^2+x+1\)的两个极值点,
则\(x_1\)和\(x_2\)是方程\(3x^2+4ax+1=0\)的两根,
故 \(x_1+x_2=-\dfrac{4 a}{3}\), \(x_1 \cdot x_2=\dfrac{1}{3}\),
又\(x_2-x_1=2\),则\((x_1-x_2 )^2=(x_1+x_2 )^2-4x_1 x_2=4\),
即 \(\dfrac{16 a^2}{9}-\dfrac{4}{3}=4\),则\(a^2=3\). -
答案 (1)\(y=2x^3+3x^2-12x+1\);(2) 极大值\(21\), 极小值\(-6\).
解析 (1)\(f'(x)=6x^2+6x+a\), \(k_{\text {切 }}=f^{\prime}(0)=a\),
又因为切线方程为\(y=-12x+1\),
所以 \(k_{\text {切 }}=-12\),得\(a=-12\),
因为切点在切线上也在曲线上,
所以\(\left\{\begin{array}{l} f(0)=-12 \times 0+1=1 \\ f(0)=b \end{array}\right.\),所以\(b=1\),
所以\(f(x)\)的解析式为\(y=2x^3+3x^2-12x+1\).
(2)\(f(x)\)定义域为\(R\),\(f'(x)=6x^2+6x-12\)
令\(f'(x)=0\)得,\(x=-2\)或\(1\),
所以在\((-∞,-2)\),\((1,+∞)\)上单调递增,在\((-2,1)\)上单调递减,
所以\(f(x)_{\text {极大值 }}=f(-2)=21\), \(f(x)_{\text {极小植 }}=f(1)=-6\). -
答案 (1) 在\((-∞,-1)\),\((1,+∞)\)上单调递增,在\((-1,1)\)上单调递减;
(2) 当\(a=-1\)时,无极值;当\(a>-1\)时,极大值为\(\dfrac{1}{2} a+\dfrac{1}{6}\),极小值为\(-\dfrac{1}{6} a^3+\dfrac{3}{2} a^2\);
当\(a<-1\)时,极小值为\(\dfrac{1}{2} a+\dfrac{1}{6}\),极大值为\(-\dfrac{1}{6} a^3+\dfrac{3}{2} a^2\).
解析 (1)当\(a=1\)时,\(f(x)= \dfrac{1}{3} x^3-x\),\(\therefore f'(x)=x^2-1\),
令\(f'(x)=0\),解得\(x=1\),或\(x=-1\),
当\(f'(x)>0\)时,即\(x>1\),或\(x<-1\)时,函数为增函数,
当\(f'(x)<0\)时,即\(-1<x<1\),函数为减函数,
\(\therefore f(x)\)\(在(-∞,-1)\),\((1,+∞)\)上单调递增,在\((-1,1)\)上单调递减;
(2) \(f'(x)=x^2-(a-1)x-a=(x-a)(x+1)\),
令\(f'(x)=0\),解得\(x=-1\)或\(x=a\),
①当\(a=-1\)时,\(f'(x)⩾0\)恒成立,\(\therefore f(x)\)单调递增,函数无极值,
②当\(a>-1\)时,
当\(f'(x)>0\)时,即\(x>a\),或\(x<-1\)时,函数为增函数,
当\(f'(x)<0\)时,即\(-1<x<a\),函数为减函数,
\(\therefore\)当\(x=-1\)时,函数有极大值,极大值为\(f(-1)=-\dfrac{1}{3}-\dfrac{1}{2}(a-1)+a=\dfrac{1}{2} a+\dfrac{1}{6}\),
当\(x=a\)时,函数有极小值,极小值为\(f(a)=\dfrac{1}{3} a^3-\dfrac{1}{2}(a-1) a^2+a^2=-\dfrac{1}{6} a^3+\dfrac{3}{2} a^2\),
③当\(a<-1\)时,
当\(f'(x)>0\)时,即\(x>-1\),或\(x<a\)时,函数为增函数,
当\(f'(x)<0\)时,即\(a<x<-1\),函数为减函数,
\(\therefore\)当\(x=-1\)时,函数有极小值,极小值为\(f(-1)=\dfrac{1}{2} a+\dfrac{1}{6}\),
当\(x=a\)时,函数有极大值,极大值为\(f(a)=-\dfrac{1}{6} a^3+\dfrac{3}{2} a^2\).
综上所述,当\(a=-1\)时,无极值;
当\(a>-1\)时,极大值为\(\dfrac{1}{2} a+\dfrac{1}{6}\),极小值为\(-\dfrac{1}{6} a^3+\dfrac{3}{2} a^2\);
当\(a<-1\)时,极小值为\(\dfrac{1}{2} a+\dfrac{1}{6}\),极大值为 \(-\dfrac{1}{6} a^3+\dfrac{3}{2} a^2\).
【B组---提高题】
1.(多选)如图,已知直线\(y=kx+m\)与曲线\(y=f(x)\)相切于两点,则\(F(x)=f(x)-kx\)有( )

A.\(1\)个极大值点,\(2\)个极小值点 \(\qquad \qquad \qquad \qquad\) B.\(2\)个零点 \(\qquad \qquad \qquad \qquad\)
C.\(0\)个零点 \(\qquad \qquad \qquad \qquad \qquad \qquad \qquad\) D.\(2\)个极小值点,无极大值点
2.已知函数\(f(x)=e^x-a\sin x\)在区间 \(\left(0, \dfrac{\pi}{3}\right)\)上有极值,则实数\(a\)的取值范围是\(\underline{\quad \quad}\) .
3.讨论函数\(f(x)=x\ln x- \dfrac{1}{2} x^2+(a-1)x(a∈R)\)的极值点的个数.
参考答案
-
答案 \(AC\)
解析 由原图可知,\(k<0\),\(m>0\),设原图中的两切点横坐标为\(a\),\(b\).
再在同一坐标系中做出\(y=f(x)\)与\(y=kx\)的图象如图:
由图可知,\(y=f(x)\)与\(y=kx\)没有公共点,
故函数\(F(x)\)没有零点.
直线\(x=n\)与\(y=f(x)\)、\(y=kx\)分别交于点\(A\)、\(B\),
则\(F(x)\)的函数值可以理解为线段\(AB\)长度;
由图可知:当\(x∈(-∞,a)\)时,\(F(x)\)单调递减;当\(x∈(a,c)\),\(F(x)\)单调递增;
当\(x∈(c,b)\)时,\(F(x)\)单调递减;当\(x∈(b,+∞)\)时,\(F(x)\)单调递增.
故\(a\),\(b\)是函数\(F(x)\)的极小值点,\(c\)是\(F(x)\))的极大值点.
故选:\(AC\).

-
答案 \(\left(1,2 e^{\frac{\pi}{3}}\right)\)
解析 \(f(x)=e^x-\operatorname{asin} x\), \(x \in\left(0, \dfrac{\pi}{3}\right)\),
则\(f'(x)=e^x-a\cos x\)
由题意得\(e^x-a\cos x=0\)在 \(\left(0, \dfrac{\pi}{3}\right)\)上有解,
即\(a=\dfrac{e^x}{\cos x}\)在 \(\left(0, \dfrac{\pi}{3}\right)\)上有解,
记\(a=\dfrac{e^x}{\cos x}\), \(x \in\left(0, \dfrac{\pi}{3}\right)\),
则\(g^{\prime}(x)=\dfrac{e^x(\sin x+\cos x)}{\cos ^2 x}\),
当\(x \in\left(0, \dfrac{\pi}{3}\right)\)时,\(g'(x)>0\),\(g(x)\)递增,
而\(g(0)=1\), \(g\left(\dfrac{\pi}{3}\right)=2 e^{\frac{\pi}{3}}\),故 \(1<a<2 e^{\frac{\pi}{3}}\). -
答案 当\(a≤1\)时,\(f(x)\)没有极值点;当\(a>1\)时,\(f(x)\)有\(2\)个极值点.
解析 \(f'(x)=\ln x-x+a\), \(f^{\prime \prime}(x)=\dfrac{1}{x}-1=\dfrac{1-x}{x}\),
当\(x∈(0,1)\)时,\(f'' (x)>0\),\(f'(x)\)单调递增;
当\(x∈(1,+∞)\)时,\(f'' (x)<0\),\(f'(x)\)单调递减,
所以当\(x=1\)时,\(f'(x)\)有极大值,\(f'(1)=a-1\),
当\(a≤1\)时,\(f'(1)≤0\),
所以\(f(x)\)在\((0,+∞)\)上单调递减,此时\(f(x)\)无极值,
当\(a>1\)时,\(f'(1)=a-1>0\),
\(f^{\prime}\left[\left(\dfrac{1}{e}\right)^{a+1}\right]=\ln \left(\dfrac{1}{e}\right)^{a+1}-\left(\dfrac{1}{e}\right)^{a+1}+a\)\(=-a-1-\left(\dfrac{1}{e}\right)^{a+1}+a=-1-\left(\dfrac{1}{e}\right)^{a+1}<0\),
易证\(x>1\)时,\(e^x>2x\),
所以\(a>1\),\(f'(e^a)=2a-e^a<0\),
故存在\(x_1\),\(x_2\)满足\(0<( \dfrac{1}{e})^{a+1}<x_1<1<x_2<e^a\),\(f'(x_1)=f'(x_2)=0\),
当\(x∈(0,x_1)\)时,\(f(x)\)单调递减,当\(x∈(x_1,x_2)\)时,\(f(x)\)单调递增,
当\(x∈(x_2,+∞)\)时,\(f(x)\)单调递减,
所以\(f(x)\)在\(x=x_1\)处有极小值,在\(x=x_2\)处有极大值.
综上所述,当\(a≤1\)时,\(f(x)\)没有极值点;当\(a>1\)时,\(f(x)\)有\(2\)个极值点.
【C组---拓展题】
1.已知函数 \(f(x)=\dfrac{e^x}{x}+k(\ln x-x)\),若\(x=1\)是函数\(f(x)\)的唯一极值点,则实数\(k\)的取值范围是\(\underline{\quad \quad}\).
参考答案
- 答案\((-∞,e]\)
解析 \(\because\)函数 \(f(x)=\dfrac{e^x}{x}+k(\ln x-x)\)的定义域是\((0,+∞)\),
\(\therefore f^{\prime}(x)=\dfrac{e^x(x-1)}{x^2}+\dfrac{k(1-x)}{x}=\dfrac{\left(e^x-k x\right)(x-1)}{x^2}\) ,
\(x=1\)是函数\(f(x)\)的唯一一个极值点,
\(\therefore x=1\)是导函数\(f'(x)=0\)的唯一根,
\(\therefore e^x-kx=0\)在\((0,+∞)\)无变号零点,
令\(g(x)=e^x-kx\),则\(g'(x)=e^x-k\),
①\(k≤0\)时,\(g'(x)>0\)恒成立,\(g(x)\)在\((0,+∞)\)时单调递增,
\(g(x)\)的最小值为\(g(0)=1\),\(g(x)=0\)无解,
②\(k>0\)时,\(g'(x)=0\)有解,为:\(x=\ln k\),
\(0<x<\ln k\)时,\(g'(x)<0\),\(g(x)\)单调递减,
\(\ln k<x\)时,\(g'(x)>0\),\(g(x)\)单调递增,
\(\therefore g(x)\)的最小值为\(g(\ln k)=k-k\ln k\),
\(\therefore k-k\ln k>0\),\(\therefore k<e\),
画出函数\(y=e^x\)和\(y=ex\)的图象,如图示:

由\(y=e^x\)和\(y=ex\)图象,它们切于\((1,e)\),
综上所述\(k≤e\),
故答案为:\((-∞,e]\).